大家好,我是Python进阶者。这篇文章的题目真的是很难取,索性先取这个了,装个13好了。
前言
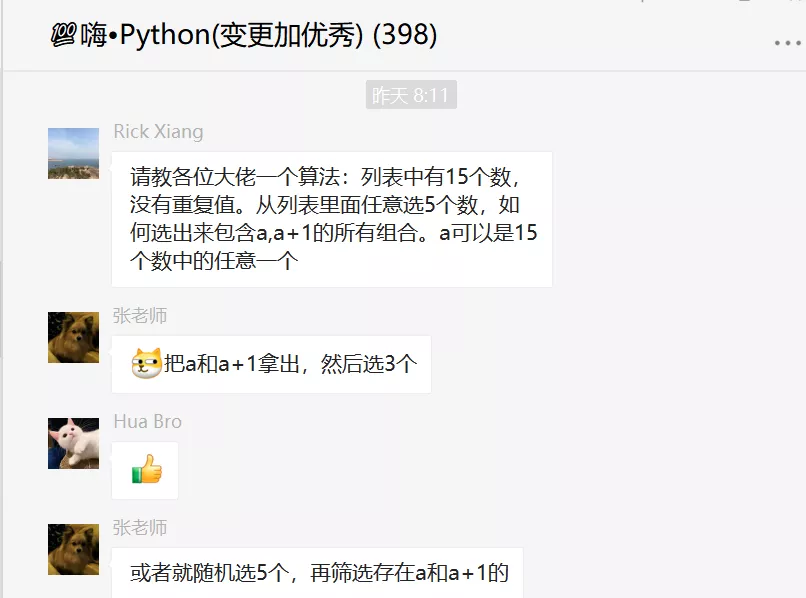
前几天在才哥交流群里,有个叫【Rick Xiang】的粉丝在Python交流群里问了一道关于排列组合的问题,初步一看觉得很简单,实际上确实是有难度的。
题目是:一个列表中有随机15个数,没有重复值。从列表里面任意选5个数,如何选出来包含a, a+1的所有组合。a可以是15个数中的任意一个。
一、思路
这个问题看似简单,思路正如上图的【张老师】说的那样,分两步走,理论上来说,确实是可以实现。正常我们计算排列组合公式,用下图中的组合公式计算是没问题的。
但是这道题目的实现,涉及到用Python程序进行实现,当然计算一个数值,对于Python和我们来说并不难,难的是需要回归排列组合原本的状态,然后用程序进行实现。本文借用了群成员【有点意思】所说的蒙特卡洛算法和代码进行实现,下面一起来看看吧!
这里引用【张老师】提及的第二种方案,先随机取14个数,然后从14个随机数中随机取一个,然后自增1,作为第15个随机数,之后再从这15个随机数中进行随机取5个随机数,再进行if判断,看看连续值是否同时存在同一个列表中,之后把满足条件的列表append到一个空列表中去,最后再去用set集合去重,得到最后的结果。
二、解决方法
1)伪代码
这里先给出【有点意思】大佬的伪代码,这样看上去大家也更加好理解一些,如下图所示。其实下面这个代码也不算是伪代码,现在Python也支持中文变量,下面这个代码也是完全可以跑起来的,只不过看上去要比下文中的纯英文代码要更加好理解一些。
下面给出具体的实现过程,这里给出5份代码,欢迎大家积极尝试。
2)代码一
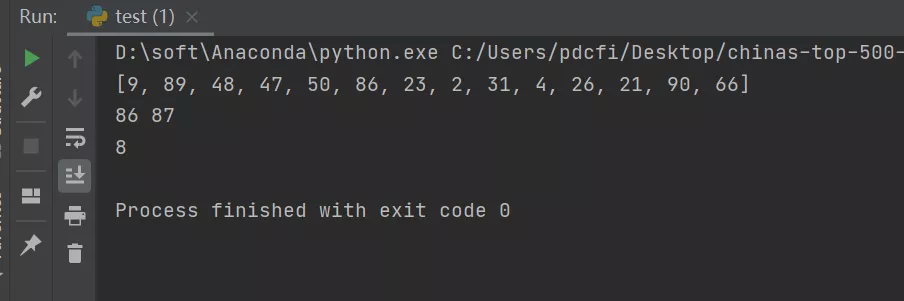
- # coding: utf-8
- import random
- def quchong(list_data):
- list2 = []
- for i in list_data:
- if i not in list2:
- list2.append(i)
- return list2
- # 从随机的15个数值中随机取出5个数,放到一个数组
- # 生成不重复的14个随机数
- random_14 = [random.randint(0, 100) for i in range(14)] # 这个写法容易出现随机值重复
- random_14 = random.sample(range(100), 14)
- print(random_14)
- random_1 = random.choice(random_14)
- random_2 = random_1 + 1
- random_14.append(random_2)
- random_15 = random_14
- print(random_1, random_2)
- final_list = []
- for i in range(100):
- select = [random.choice(random_15) for j in range(5)]
- quchong_select = set(select)
- if random_1 in quchong_select and random_2 in quchong_select:
- final_list.append(quchong_select)
- fina_result = quchong(final_list)
- print(len(fina_result))
乍一看,这个方法确实可以实现,但是这里会有一个小bug,那就是random.randint()函数生成的随机中会有重复值,而题目要求是生成不重复的随机值。那么这个问题,将在代码二中得到解决。
3)代码二
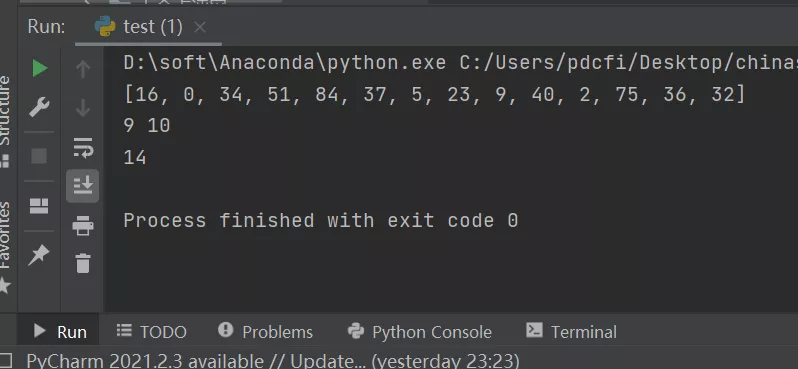
使用random.sample()函数,这个函数可以随机产生随机值,而且不会重复,还是很奈斯的。另外,使用了numpy.random.choice()函数,可以直接选择随机的5个数,效率比代码一更高一些。
- # -*- coding: utf-8 -*-
- import numpy as np
- import random
- def quchong(list_data):
- list2 = []
- for i in list_data:
- if i not in list2:
- list2.append(i)
- return list2
- # 从随机的15个数值中随机取出5个数,放到一个数组
- # 生成不重复的14个随机数
- random_14 = random.sample(range(100), 14)
- print(random_14)
- random_1 = random.choice(random_14)
- random_2 = random_1 + 1
- random_14.append(random_2)
- random_15 = random_14
- print(random_1, random_2)
- final_list = []
- for i in range(100):
- sub_random_data = np.random.choice(random_15, 5)
- quchong_select = set(sub_random_data)
- if random_1 in quchong_select and random_2 in quchong_select:
- final_list.append(quchong_select)
- fina_result = quchong(final_list)
- print(len(fina_result))
4)代码三
代码三主要是在代码一和代码二的基础上加了一些函数,使得读起来更加的有逻辑性和层次感。
- # -*- coding: utf-8 -*-
- # 模块化
- import random
- import numpy as np
- # 从随机的15个数值中随机取出5个数,放到一个数组,生成不重复的14个随机数
- def get_random15():
- random_14 = random.sample(range(1000), 14)
- print(random_14)
- random_1 = random.choice(random_14)
- random_2 = random_1 + 1
- random_14.append(random_2)
- random_15 = random_14
- print(random_1, random_2)
- get_final_result(random_1, random_2, random_15)
- def get_final_result(random_1, random_2, random_15):
- final_list = []
- for i in range(1000):
- sub_random_data = np.random.choice(random_15, 5)
- quchong_select = set(sub_random_data)
- if random_1 in quchong_select and random_2 in quchong_select:
- final_list.append(quchong_select)
- fina_result = quchong(final_list)
- print(len(fina_result))
- def quchong(list_data):
- list2 = []
- for i in list_data:
- if i not in list2:
- list2.append(i)
- return list2
- if __name__ == '__main__':
- get_random15()
5)代码四
细心的朋友可能已经发现了一个问题,在随机从np.random.choice(random_15, 5)取值的时候,也会取出重复的值,这样也是不符合要求的,这里给出了一个方案,从15个随机数中取出一个之后,然后remove掉这个取出的数,重新去剩下的列表中去取,这样就完美的避开了这个问题。
- # 模块化
- import random
- import numpy as np
- # 取出随机的15个数值
- def get_random15():
- for i in range(2):
- random_15 = random.sample(range(20), 15)
- # print(random_15)
- get_random5(random_15)
- # 遍历随机的15个数值,取相邻的两个随机数,并调用函数进行处理
- def get_random5(random_15):
- random_5 = []
- # 遍历5次,从random_15中取5个不同的元素
- for i in range(5):
- random_data = np.random.choice(random_15)
- random_5.append(random_data)
- random_15.remove(random_data)
- # print(random_5)
- for num in random_5:
- random_1 = num
- random_2 = random_1 + 1
- get_final_result(random_1, random_2, random_5)
- # 判断相邻的两数值是否同时存在随机的15个数值的列表中,如果满足要求,就存到一个列表中,并调用去重函数
- def get_final_result(random_1, random_2, random_5):
- final_list = []
- if random_1 in random_5 and random_2 in random_5:
- print(random_5)
- final_list.append(random_1)
- result = quchong(final_list)
- print(result)
- # 针对得到的所有列表,进行去重处理
- def quchong(list_data):
- list = []
- for i in list_data:
- if i not in list:
- list.append(i)
- return list
- if __name__ == '__main__':
- get_random15()
代码写到这里,已经比之前的方案要好很多了,比之前的三个代码都要严谨一些,但是仍然存在不足。虽然解决了随机生成重复性的问题,也解决了随机从random_15中取出重复数的问题,但是弊端还是存在的。这个代码遍历挺多的,复杂度倒是正常,但是输出的格式不太好看,没有达到预期。这里我只是遍历了2次,而且随机数我只是开放到0-20,如果循环次数增多,数值越多的话,计算起来速度可就不好说了。
6)代码五
经过【有点意思】大佬和我的共同努力,现在祭出终极版本,这个版本是迄今为止,针对该问题写出的最严谨的一个版本了,代码如下。
- # -*- coding: utf-8 -*-
- # 模块化
- import random
- import numpy as np
- import time
- # 取出随机的15个数值
- def get_random15():
- for i in range(100000):
- random_15 = random.sample(range(2000), 15)
- # print("随机15数=",random_15,len(random_15))
- get_random5(random_15)
- # 遍历随机的15个数值,取相邻的两个随机数,并调用函数进行处理
- def get_random5(random_15):
- random_5 = []
- # 遍历5次,从random_15中取5个不同的元素
- for i in range(5):
- random_data = np.random.choice(random_15)
- random_5.append(random_data)
- random_15.remove(random_data)
- # print("random_5=",random_5)
- # print("random_15=",random_15)
- for num in random_5:
- random_1 = num
- random_2 = random_1 + 1
- # print(random_1,random_2)
- get_final_result(random_1, random_2, random_5)
- # 判断相邻的两数值是否同时存在随机的15个数值的列表中,如果满足要求,就存到一个列表中,并调用去重函数
- def get_final_result(random_1, random_2, random_5):
- final_list = []
- if random_1 in random_5 and random_2 in random_5:
- # print(random_5)
- final_list.append(random_5)
- result = quchong(final_list)
- if result:
- if len(result[0]) == 5:
- # print(random_1,random_2)
- # print("result=",result)
- final_result.append(result)
- # 针对得到的所有列表,进行去重处理
- def quchong(list_data):
- list = []
- for i in list_data:
- if i not in list:
- list.append(i)
- return list
- if __name__ == '__main__':
- start_time = time.time()
- global final_result
- final_result = []
- get_random15()
- final_result = quchong(final_result)
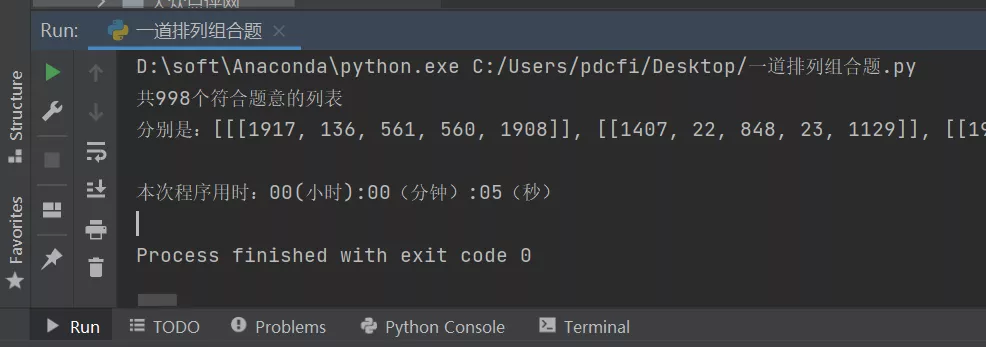
- print("共%d个符合题意的列表" % len(final_result))
- print("分别是:%s" % final_result)
- end_time = time.time()
- used_time = end_time - start_time
- print()
- print("本次程序用时:{}".format(time.strftime('%H(小时):%M(分钟):%S(秒)', time.gmtime(used_time))))
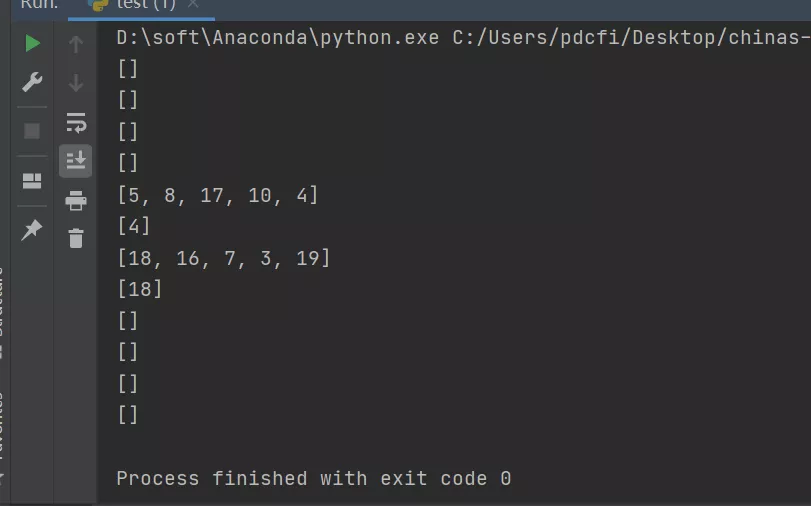
这个代码运行之后,可以看到符合题意列表的具体个数,还有具体的列表数值,还有耗时时间。
经过测试,在10万次循环以内,符合要求的数据大概有1000左右,运行时间也只是秒级的。如果继续扩大循环力度,程序的复杂度会更加大,更加贴近理论的排列组合值,因为耗时太长,这里不再做测试,感兴趣的话,自己可以改下参数进行调试。
三、总结
我是Python进阶者。本文基于粉丝针对排列组合问题的提问,给出了一个利用Python基础+蒙特卡洛算法的解决方案,基本上可以达到了粉丝的要求。
不过话说回来,这个方案还是存在一定的弊端的,随着循环次数越多,随机数越大,排列组合数就会越多,运行的时间也就会越长,当然得到的数据也就更加的精准了。