有过编程经验的同学,对于移位操作应该很熟悉了,日常工作中或多或少都有用到,当 移位位数是负数 或者 移位位数超过了 类型的最大二进制位时,和正常移位处理是不一样的,下面将详细说明这两种情况,在此之前,先了解下正常的移位操作
正数的左移和右移
正数的左移是二进制位向左移动,右边留空的位置补 0,右移是二进制位向右移动,左边留空的位置补 0 ( 符号位为 0 )
- 左移
左移操作,最高位的符号位会出现 0 或 1 , 因此结果会出现正数和负数的情况
新建测试文件 base.cpp,代码如下
- #include <stdint.h>
- #include <iostream>
- using namespace std;
- int32_t main(int32_t argc , char *argv[])
- {
- int32_t a = 7;
- cout << "(a << 2) = " << (a << 2) << endl;
- cout << "(a << 30) = " << (a << 30) << endl;
- return 0;
- }
执行 g++ -g -Wall -std=c++11 -o base base.cpp 命令编译代码,再执行 ./base 运行程序,结果如下
- (a << 2) = 28
- (a << 30) = -1073741824
上述代码中,变量 a 的值为 7,对应的二进制是 0000 0000 0000 0000 0000 0000 0000 0111
左移 2 位:二进制向左移动 2 位,右边补充 2 位 0 ,左边丢弃超出的 2 位二进制, 结果是 0000 0000 0000 0000 0000 0000 0001 1100, 对应的十进制数是 28
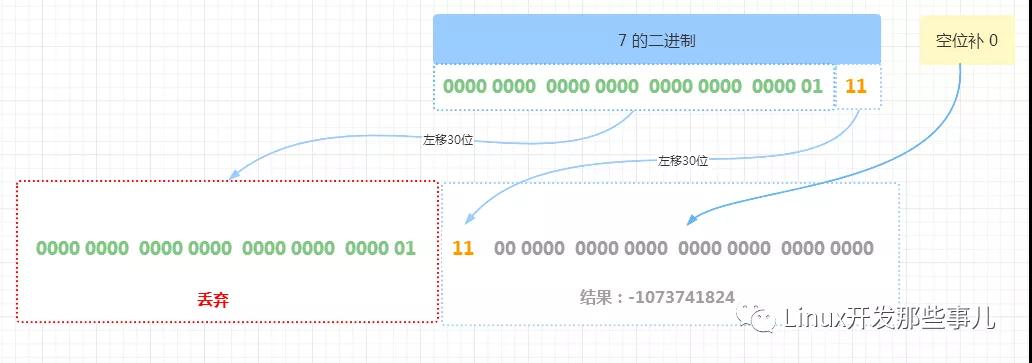
左移 30 位 的流程如下图
由上图可知,二进制向左移动 30 位后, 左边 30 位二进制 0000 0000 0000 0000 0000 0000 0000 01 因超出被丢弃,同时最右边剩下的 2 位二进制 11 左移 30 位,右边空的位置补充 30 位 0,最终的结果是 1100 0000 0000 0000 0000 0000 0000 0000, 对应的十进制数是 -1073741824
可以看出,正数 7 左移 30 位后,二进制的符号位变成了 1 ,也即正数变成了负数了
- 右移
正数右移,最小为 0 , 不会出现负数,下面是右移的测试代码
修改 base.cpp 文件,代码如下
- #include <stdint.h>
- #include <iostream>
- using namespace std;
- int32_t main(int32_t argc , char *argv[])
- {
- int32_t a = 7;
- cout << "(a >> 1) = " << (a >> 1) << endl;
- cout << "(a >> 31) = " << (a >> 31) << endl;
- return 0;
- }
编译并运行上面程序,结果如下:
- (a >> 1) = 3
- (a >> 31) = 0
上述实例代码中,变量 a 的值为 7,对应的二进制是 0000 0000 0000 0000 0000 0000 0000 0111
右移 1 位:二进制向右移动 1 位,左边补充一位 0 ,右边丢弃超出的一位二进制, 结果是 0000 0000 0000 0000 0000 0000 0000 0011, 对应的十进制数是 3
右移 31 位:二进制向右移动 31 位,左边补充 31 位 0 ,右边丢弃超出的 31 位二进制,结果是 0000 0000 0000 0000 0000 0000 0000 0000, 对应的十进制是 0
负数的左移和右移
负数的左移是二进制位向左移动,右边留空的位置补 0,右移是二进制位向右移动,左边留空的位置补 1 ( 符号位为 1 ),这一点跟正数是不一样的
计算机中是用补码的形式进行各种运算的,正数的补码是其自身,负数的补码是将其正数按位取反加 1
- 左移
负数左移,符号位可能会变成0,因此结果会出现正数和负数的情况,一直左移的话,最终会变成 0
修改 base.cpp文件,代码如下
- #include <stdint.h>
- #include <iostream>
- using namespace std;
- int32_t main(int32_t argc , char *argv[])
- {
- int32_t b = -3;
- cout << "(b << 1) = " << (b << 1) << endl;
- cout << "(b << 30) = " << (b << 30) << endl;
- return 0;
- }
编译并运行上面程序,结果如下:
- (b << 1) = -6
- (b << 30) = 1073741824
上面代码中,变量 b 的值为 -3,对应的二进制是 1111 1111 1111 1111 1111 1111 1111 1101
左移 1 位:整个二进制串向左移动 1 位,右边补充 0 ,左边丢弃超出的一位二进制,结果是 1111 1111 1111 1111 1111 1111 1111 1010,对应十进制数 -6
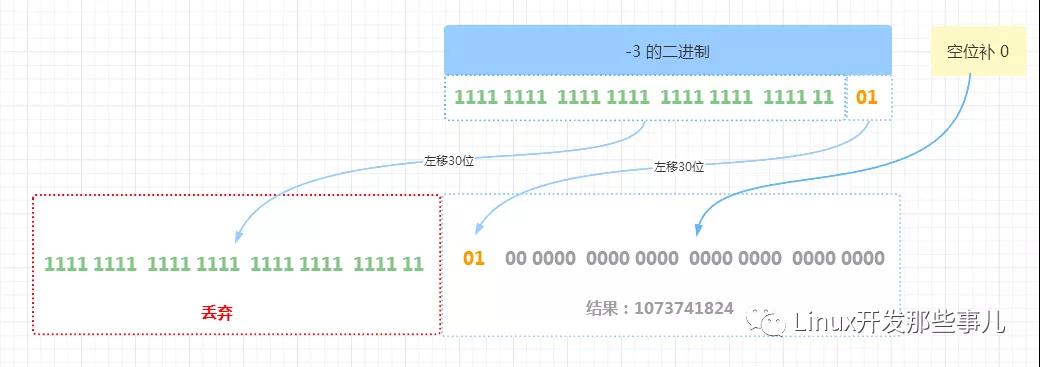
左移 30 位 的流程如下
由上图可知,左移 30 位,左边的 30 位二进制 1111 1111 1111 1111 1111 1111 1111 11 因超出数值最大位数而被丢弃,原来最右边的 01 移到了最左边,紧接着后面的 30 个空位全部补 0 ,最终的结果是 0100 0000 0000 0000 0000 0000 0000 0000 ,对应十进制是 1073741824
可以看出,负数 -3 左移 30 位后,二进制的符号位变成了 0 ,由开始的负数变成了正数了
- 右移
负数右移是在左边补 1, 所以结果不会出现正数的情况,如果一直右移,最终二进制位会全部变成 1,即十进制的 -1 ( 二进制全 1 在补码中表示 -1 )
修改 base.cpp,代码如下
- #include <stdint.h>
- #include <iostream>
- using namespace std;
- int32_t main(int32_t argc , char *argv[])
- {
- int32_t b = -3;
- cout << "(b >> 1) = " << (b >> 1) << endl;
- cout << "(b >> 31) = " << (b >> 31) << endl;
- return 0;
- }
编译并运行上面程序,结果如下:
- (b >> 1) = -2
- (b >> 31) = -1
上面代码中,变量 b 的值为 -3,对应的二进制是 1111 1111 1111 1111 1111 1111 1111 1101
右移 1 位:二进制位向右移动 1 位,左边补充 1 ,右边丢弃一位超出的二进制,结果为 1111 1111 1111 1111 1111 1111 1111 1110,对应的十进制是 -2
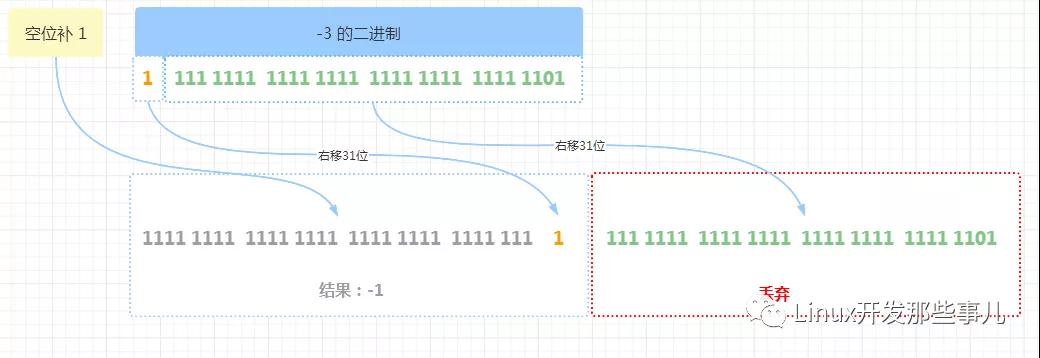
右移 31 位 的流程如下
根据上图可知,右移 31 位,最右边的 31 位二进制 1111 1111 1111 1111 1111 1111 1111 110 因超出数值最大位数而被丢弃, 原来左边的 1 移到了最右边,左边补 31 位 1,最后结果为:1111 1111 1111 1111 1111 1111 1111 1111 , 对应的十进制数 -1
移位数超过类型最大位数
移位的位数大于等于数值类型的最大位数时,实际的移的位数是:移位的位数和该类型的最大位数做取模运算,余数就是要移的位数,不管左移还是右移,这种方法都适用
比如:类型为 int32_t,移位的位数是 34,实际移位的位数为:34 % 32 = 1
修改 base.cpp 文件,内容如下:
- #include <stdint.h>
- #include <iostream>
- using namespace std;
- int32_t main(int32_t argc , char *argv[])
- {
- int32_t a = 7;
- cout << "(a >> 32) = " << (a >> 32) << endl;
- cout << "(a >> 33) = " << (a >> 33) << endl;
- cout << "(a << 34) = " << (a << 34) << endl;
- return 0;
- }
编译并执行,结果如下
- (a >> 32) = 7
- (a >> 33) = 3
- (a << 34) = 28
变量 a 的值为 7,对应的二进制是 0000 0000 0000 0000 0000 0000 0000 0111
右移 32 位:因移位位数等于 int32_t 最大位数,所以实际移位数为 32 % 32 = 0,右移 0 位 表示没有移位,所以结果还是 7
右移 33 位:移位位数大于 int32_t 最大位数,故实际移位数为 33 % 32 = 1,右移 1 位,左边补 0 ,右边丢弃超出的位,结果是: 0000 0000 0000 0000 0000 0000 0000 0011,对应的十进制是 3
左移 34 位:移位位数大于 32 ,实际移位数为 34 % 32 = 2,左移 2 位,右边补 0 ,左边丢弃超出的位,结果是:0000 0000 0000 0000 0000 0000 0001 1100,对应的十进制是 28
正常情况下,在移位数相同时,分几次移位操作和单次移位操作的结果是一样的, 比如:一个 int32_t 变量,值为 7, 7 << 1 << 2 和 7 << 3 的结果相同的
当移位数大于等于数值类型最大位数时,上述的结果是不一样的,比如:一个 int32_t 变量,值为 7, 虽然 7 << 33 和 7 << 20 << 13 两者移位数都是 33,但结果却是不同的,前者是 14,而后者是 0
移位的位数是负值
当移位的位数是负值时,实际移位的位数是:用被移位数值类型的最大位数和移位位数相加,如果结果还是负数,结果继续 加上被移位数值类型的最大位数,直到结果不为负数为止,此时的结果即为最终移位的位数
比如:被移位的数据类型是 int32_t,移位位数是 -31,最终移位的位数是:32 + ( -31 ) = 1
当移位位数是 -60,计算最终移位位数,32 + ( -60 ) = -28,由于结果还是负数,所以继续相加,32 + ( -28 ) = 4,此次结果不为负数了,所以最终移位的位数是 4
修改 base.cpp 文件,内容如下:
- #include <stdint.h>
- #include <iostream>
- using namespace std;
- int32_t main(int32_t argc , char *argv[])
- {
- int32_t a = 7;
- cout << "(a >> -31) = " << (a >> -31) << endl;
- cout << "(a << -60) = " << (a >> -60) << endl;
- return 0;
- }
编译代码并执行,结果如下
- (a >> -31) = 3
- (a >> -60) = 0
变量 a 的值为 7,对应的二进制是 0000 0000 0000 0000 0000 0000 0000 0111
右移 -31 位:移位数是负数,实际右移 32 + ( -31 ) = 1 位,结果为:0000 0000 0000 0000 0000 0000 0000 0011,对应的十进制是 3
右移 -60 位:移位数是负数,实际右移 32 + 32 + ( -60 ) = 4 位,结果为:0000 0000 0000 0000 0000 0000 0000 0000,对应的十进制是 0
小结
本文主要介绍了左移和右移操作,左移相当于乘以 2 的 N 次方,而右移相当于除以 2 的 N 次方,这里的 N 表示移位的位数,需要注意的是,当移位位数是负数或者大于等于类型最大位数时,编译器对他们的处理和正常的移位是不一样的