鱼和熊掌不可兼得？清华团队提出高准确率的可解释分类模型-鱼和熊掌不可兼得逻辑

清华大学（第一作者为王建勇教授的在读博士生王焯）联合华东师范大学（张伟，2016 年博士毕业于清华大学）和山东大学（刘宁，2021 年博士毕业于清华大学）提出了一种基于规则表征学习的分类模型 RRL。RRL 同时具备类似决策树模型的高可解释性和类似随机森林和 XGBoost 等集成学习器的分类性能。相关论文已入选 NeurIPS2021。

论文链接：https://arxiv.org/abs/2109.15103
代码链接：https://github.com/12wang3/rrl

为了同时获得良好的可解释性和分类性能，论文提出了一种新的分类模型——规则表征学习器（RRL）。RRL 能够通过自动学习可解释的非模糊规则进行数据表征和分类。为了高效地训练不可导的 RRL 模型，论文提出了一种新的训练方法——梯度嫁接法。借助梯度嫁接法，离散的 RRL 可以直接使用梯度下降法进行优化。此外，论文还设计了一种改进版的逻辑激活函数，既提高了 RRL 的可扩展性，又使其能够端到端地离散化连续特征。

在九个小规模和四个大规模数据集上的实验表明，RRL 的分类性能显著优于其他可解释方法（如第二届「AI 诺奖」得主 Cynthia Rudin 教授团队提出的 SBRL），并能与不可解释的复杂模型（如集成学习模型随机森林和 XGBoost、分段线性神经网络 PLNN）取得近似的分类性能。此外，RRL 能够方便地在分类精度和模型复杂度之间进行权衡，进而满足不同场景的需求。

研究背景与动机

尽管深度神经网络已在很多机器学习任务中取得了令人瞩目的成果，其不可解释的特性仍使其饱受诟病。即使人们可以使用代理模型（Surrogate Models），隐层探查法（Hidden Layer Investigation），以及其他事后（Post-hoc）方法对深度网络进行解释，这些方法的忠实度、一致性和具体程度都存在或多或少的问题。

反观基于规则的模型（Rule-based Model），例如决策树，得益于其透明的内部结构和良好的模型表达能力，仍在医疗、金融和政治等对模型可解释性要求较高的领域发挥着重要作用。然而，传统的基于规则的模型由于其离散的参数和结构而难以优化，尤其在大规模数据集上，这严重限制了规则模型的应用范围。而集成模型、软规则和模糊规则等，虽然提升了分类预测能力，但牺牲了模型可解释性。

为了在更多场景中利用规则模型的优势，迫切需要解决以下问题：如何在保持可解释性的同时提高基于规则的模型的可扩展性？

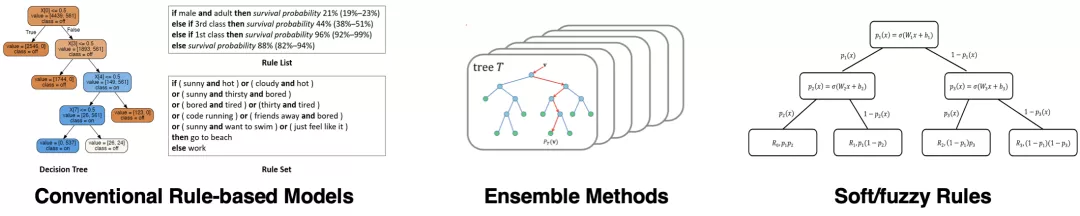
图 1：传统的基于规则的模型及其拓展模型

规则表征学习器

为了解决以上问题，论文提出了一种新的基于规则的模型，规则表征学习器（Rule-based Representation Learner, RRL），用于可解释分类任务。为了获得良好的模型透明度和表达能力，RRL 被设计为一个层级模型（如图 2 所示），由一个二值化层，若干逻辑层，一个线性层，以及层与层之间的连边构成：

二值化层（Binarization Layer）

用于对连续值特征进行划分。
结合逻辑层可实现特征端到端离散化。

逻辑层（Logical Layer）

用于自动学习规则表征。
每个逻辑层由一个合取层和一个析取层构成。
两层逻辑层即可表示合取范式和析取范式。

线性层（Linear Layer）

用于输出分类结果。
可以更好地拟合数据的线性部分.
权重可用于衡量规则重要度。

跳连接（Skip Connection）

用于自动跳过不必要的层。

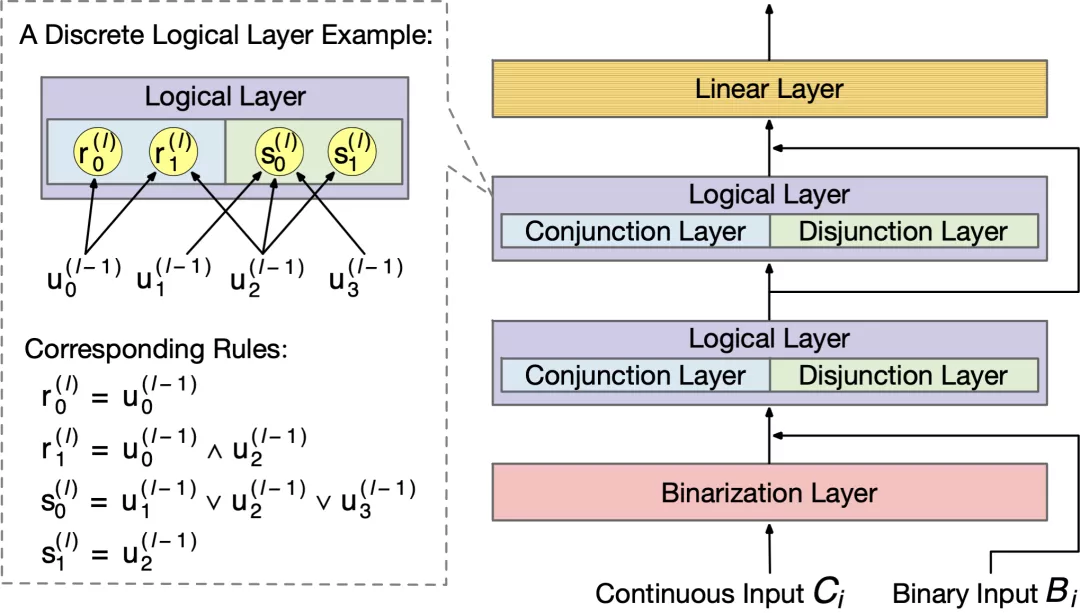
图 2：规则表征学习器举例。虚线框中展示了一个离散逻辑层及其对应的规则。

逻辑层

逻辑层（Logical Layer）使用逻辑规则自动学习数据表征。为了实现这一点，逻辑层被设计为同时具有离散版本和连续版本。二者共用参数，但离散版本用于训练、测试和解释，而连续版本仅用于训练。

离散逻辑层

逻辑层中的每个节点都代表了一个逻辑运算，包括合取和析取，而层与层之间边的连接则指明了运算有哪些变量参与。离散逻辑层节点对应的逻辑运算如下，其中

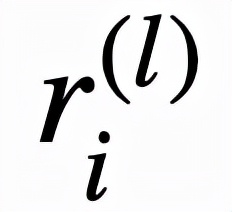
和

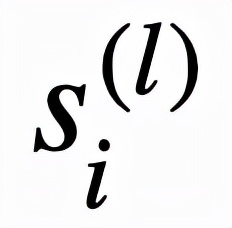
分别为合取层和析取层中的节点，

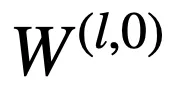
和

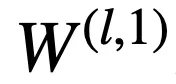
则是邻接矩阵。图 2 虚线框中展示了一个离散逻辑层的具体例子。

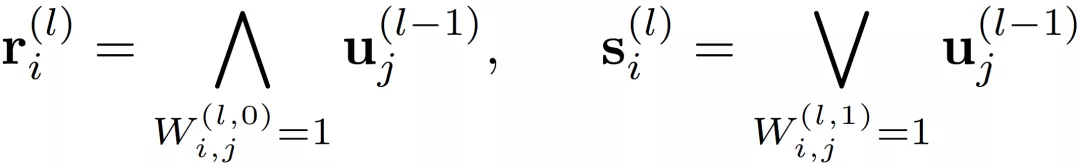
通过学习边的连接，逻辑层便可以灵活地表示有着合取或析取范式形式的离散分类规则。然而问题在于，虽然离散的逻辑层可解释性好，但自身不可导，难以训练，这也是为什么还需要一个对应的连续版本的逻辑层。

连续逻辑层

连续逻辑层必须是可导的，并且当二值化连续逻辑层的参数时，可以直接得到它相对应的离散逻辑层。为此需要：

将 0/1 邻接矩阵替换为 [0, 1] 之间的实数权重矩阵
用逻辑激活函数替换逻辑运算

传统的逻辑激活函数（Payani and Fekri, 2019）如下，其中

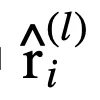
和

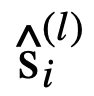
分别为连续合取层和连续析取层中的节点。

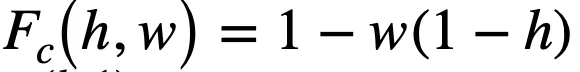
而

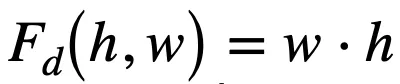
，二者通过

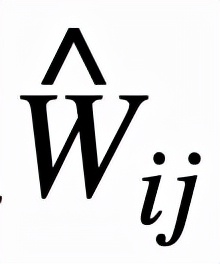
的大小来决定

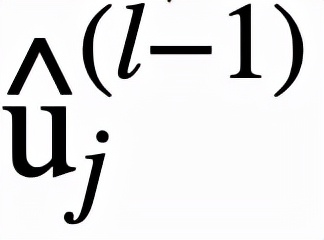
对最终结果的影响的大小。

如果

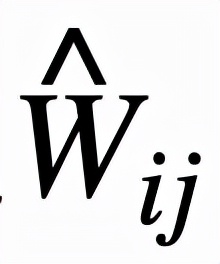
=0，则

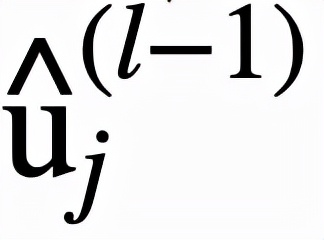
对最终结果没有影响。

虽然这两个逻辑激活函数能够较好地用可导的实数运算模拟逻辑运算，但其存在严重的梯度消失问题，无法处理特征数较多的情况，可扩展性较差。分析逻辑激活函数

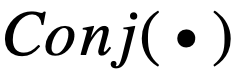
和

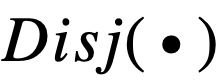
以及相应的导数可以发现，使用连乘来模拟逻辑运算是导致梯度消失的主要原因。

以

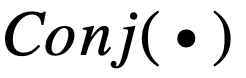
为例，其对应导数如下：

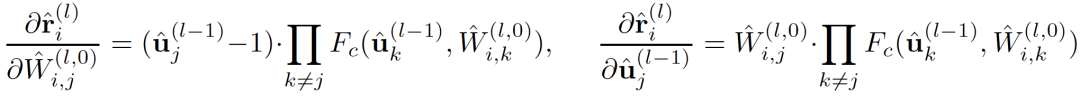
由于

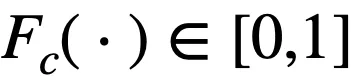
，则当相乘的

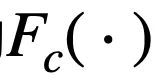
数量较多时（一般指特征数较多或节点数较多），导数结果都会趋向于 0，即出现了梯度消失的问题。

逻辑激活函数改进

传统逻辑激活函数因为使用连乘模拟逻辑运算，因而在处理较多特征时会产生梯度消失的问题，严重损害了模型的可扩展性。一个直接的改进思路是使用对数函数将连乘转化为连加。然而对数函数使得激活函数无法保持逻辑运算的特性。因而需要一个映射函数

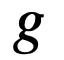
，该映射函数至少需要满足以下三个条件：

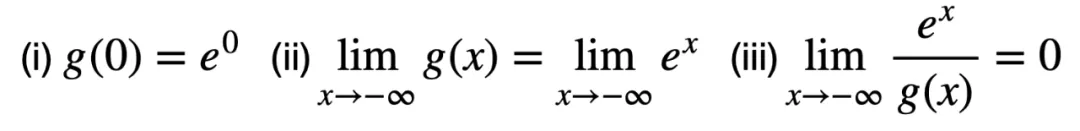
条件 (i) 和(ii)用于保持逻辑激活函数的范围和趋势，而条件 (iii) 要求

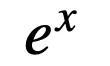
是

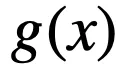
的高阶无穷小，主要用于减缓当

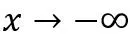
时其趋向于 0 的速度。

取

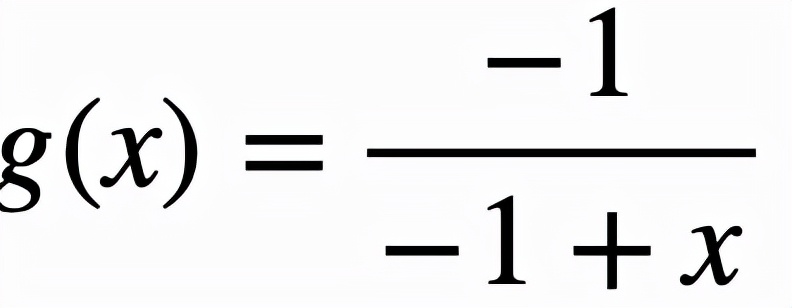
，这样对逻辑激活函数的改进可以

总结为

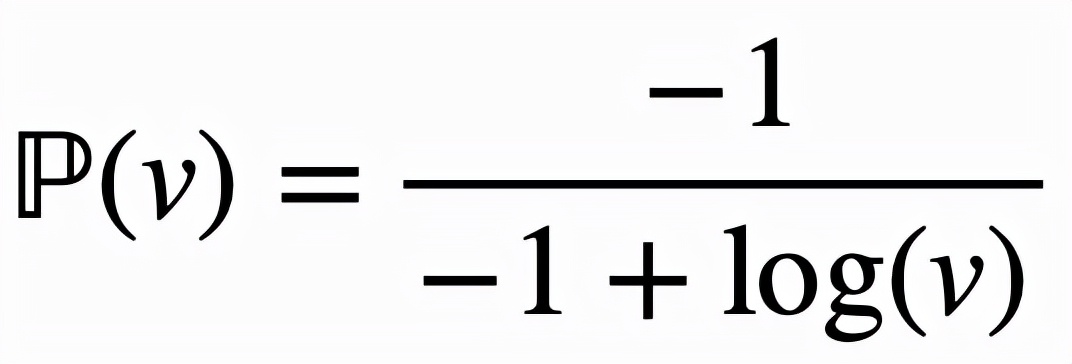
，而改进后的逻辑激活函数为：

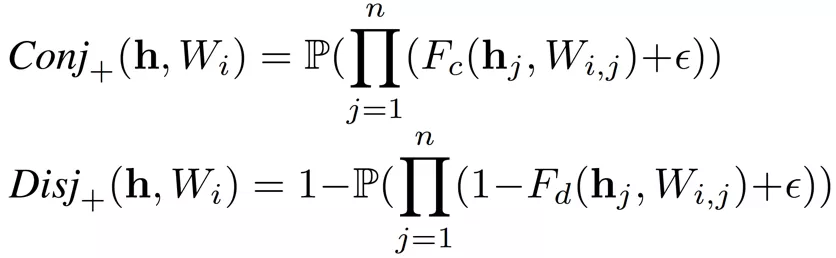
二值化层

二值化层主要用于将连续的特征值划分为若干个单元。对于第 j 个连续值特征

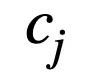
，有 k 个随机下界

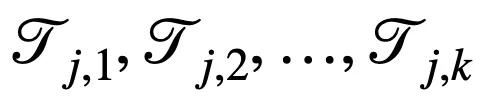
和 k 个随机上界

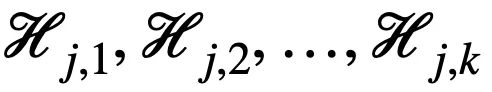
对其进行划分，进而得到以下二值向量

，其中

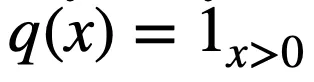
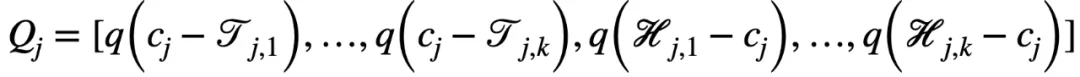
由于逻辑层的边的连接是可以学习的，因此通过组合一个二值化层和一个逻辑层，模型可以实现自动选择适当的边界进行特征离散化（二值化），即以端到端的方式对特征进行二值化。例如：

当一个合取层节点连接了和，其表示区间
当一个析取层节点连接了和，其表示区间

梯度嫁接法

虽然连续值版本的逻辑层能够使得整个 RRL 可导，但是在连续空间内搜索一个离散值解仍是一个巨大的挑战。此外，逻辑激活函数的特性导致 RRL 在离散点处的梯度几乎不含有用的信息，因此像 Straight-Through Estimator (STE)这类方法无法训练 RRL。

为了高效地对不可导的 RRL 进行训练，论文提出了一种新的基于梯度的离散模型训练方法，梯度嫁接法。在植物嫁接中（如图 3a 所示），一种植物的枝或芽作为接穗，而另一种植物的根或茎作为砧木，嫁接到一起，则得到了一种结合了二者优点的「新植物」。梯度嫁接法（Gradient Grafting）受植物嫁接方式的启发，将损失函数对离散模型的输出的梯度作为接穗，连续模型的输出对模型参数的梯度作为砧木，进而构造出了一条完整的从损失函数到参数的反向传播路径（如图 3b 所示）。令

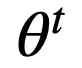
为 t 时刻的参数，

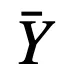
和

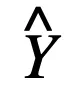
分别为离散模型和连续模型的输出，则：

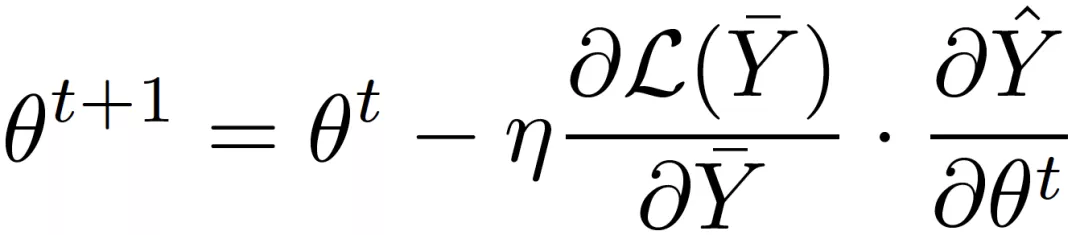
梯度嫁接法同时使用了参数空间中连续点和离散点处的梯度信息，并通过对两者的拆分组合，实现了对离散模型的直接优化。

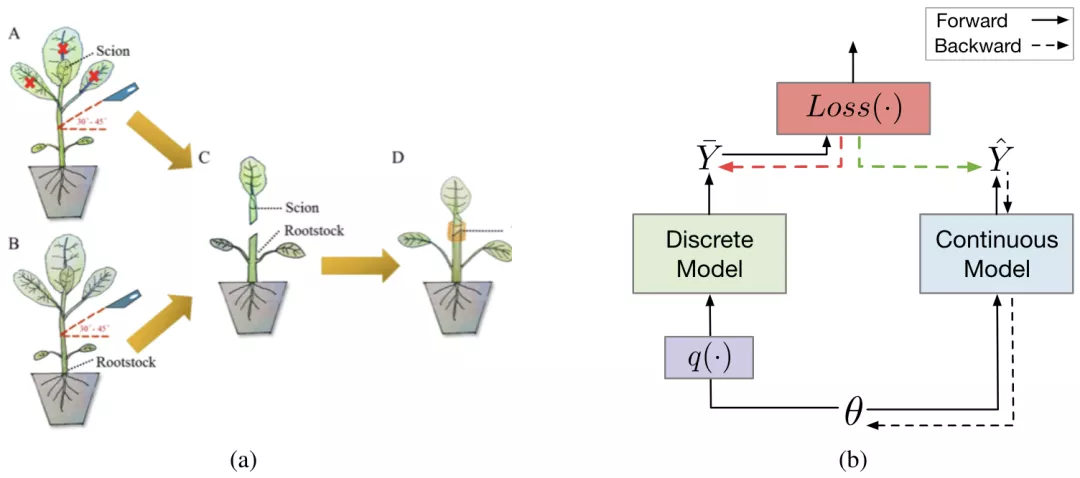
图 3：(a) 植物嫁接示例（Chen et al., 2019）。(b) 梯度嫁接法的简化计算图。实线和虚线箭头分别表示正向和反向传播。绿色箭头代表嫁接的梯度，它是红色箭头代表的梯度的一个拷贝。嫁接后，损失函数和参数之间存在一条反向传播路径。

实验

论文通过实验来评估 RRL 并回答了如下问题：

RRL 的分类性能和模型复杂度如何？
相较于其他离散模型训练方法，梯度嫁接法收敛如何？
改进后的逻辑激活函数的可扩展性如何？

作者在 9 个小规模数据集和 4 个大规模数据集上进行了实验。这些数据集被广泛用于测试模型的分类效果以及可解释性。表 1 总结了这 13 个数据集的基本信息，可以看出，这 13 个数据集充分体现了数据的多样性：实例数从 178 到 102944，类别数从 2 到 26，原始特征数从 4 到 4714。此外，数据集的特征类型和稀疏程度也各有差异。

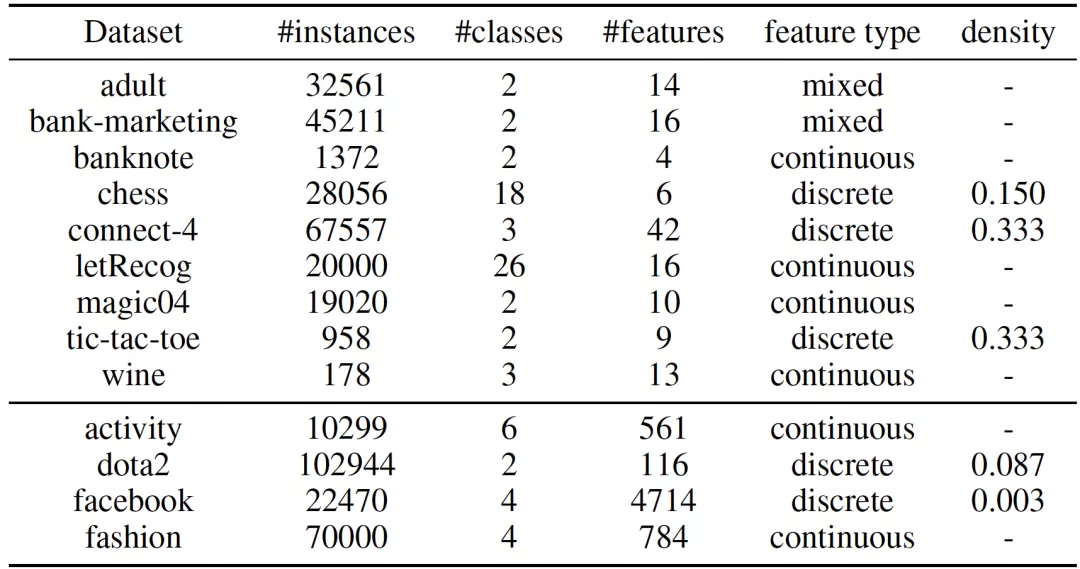
表 1：数据集统计信息

分类效果

论文将 RRL 的分类效果（F1 Score）与六个可解释模型以及五个复杂模型进行了对比，结果如表 2 所示。其中 C4.5（Quinlan, 1993）， CART（Breiman, 2017），Scalable Bayesian Rule Lists（SBRL）（Yang et al., 2017），Certifiably Optimal Rule Lists（CORELS）（Angelino et al., 2017）和 Concept Rule Sets（CRS）（Wang et al., 2020）是基于规则的模型，而 Logistic Regression（LR）（Kleinbaum et al., 2002）是一个线性模型。这六个模型被认为是可解释的。Piecewise Linear Neural Network（PLNN）（Chu et al., 2018）， Support Vector Machines（SVM）（Scholkopf and Smola, 2001），Random Forest（Breiman, 2001），LightGBM（Ke et al., 2017）和 XGBoost（Chen and Guestrin, 2016）被认为是难以解释的复杂模型。PLNN 是一类使用分段线性激活函数的多层逻辑感知机（Multilayer Perceptron, MLP）。RF，LightGBM 和 XGBoost 均为集成模型。

可以看出，RRL 显著优于其他可解释模型，只有两个复杂模型，即 LightGBM 和 XGBoost 有着相当的结果。此外，RRL 在所有数据集上均取得了较好的结果，这也证明了 RRL 良好的可扩展性。

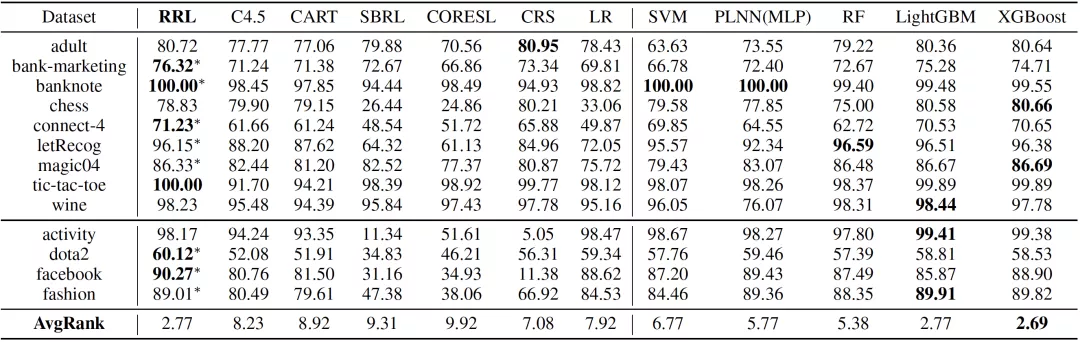
表 2：13 个数据集上各模型的分类效果（五折交叉验证的 F1 Score）

模型复杂度

可解释模型追求在确保准确率可接受的前提下，尽可能降低模型复杂度。如果模型分类效果太差，那么再低的模型复杂度也没有意义。因此，从业人员真正关心的是模型分类效果与复杂度之间的关系。

考虑到存在规则复用的情况，论文使用边的总数而不是规则总数来衡量基于规则的模型的复杂度（可解释性）。RRL，CART，CRS 以及 XGBoost 的模型复杂度与模型分类效果之间的关系如图 4 所示，其中横轴为复杂度，纵轴为分类效果。可以看出，相比其他规则模型和集成模型，RRL 能够更加高效地利用规则，即用更低的模型复杂度获得更好的分类效果。结果还表明，通过参数设置，RRL 可以轻松地在模型复杂度和分类性能间进行权衡。

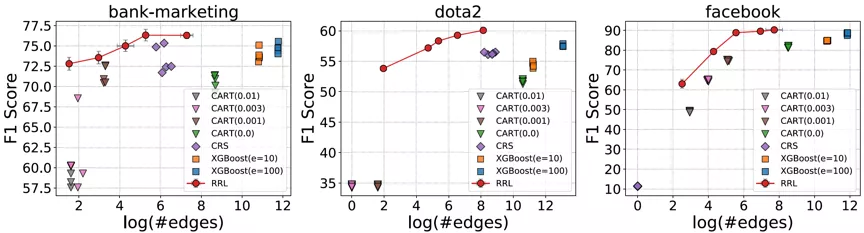
图 4：RRL 与基线模型的模型复杂度与分类效果散点图。

消融实验

离散模型训练方法

通过训练结构相同的 RRL，作者将梯度嫁接法与 STE（Courbariaux et al., 2015, 2016），ProxQuant（Bai et al., 2018）以及 RB（Wang et al., 2020）这三类离散模型训练方法进行了对比，训练损失函数结果如图 5 所示。由于 RRL 本身特殊的结构（即在离散点处的梯度具有极少的信息），只有使用梯度嫁接法训练的 RRL 才能够很好的收敛。

改进的逻辑激活函数

改进前后的逻辑激活函数的结果同样在图 5 中展示。可以看出，当处理大规模数据时，逻辑激活函数会发生梯度消失的问题，从而导致不收敛。而改进后的逻辑激活函数则克服了该问题。

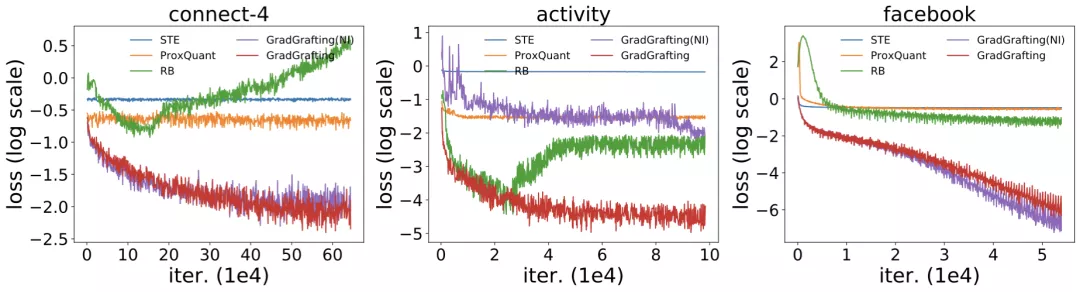
图 5：梯度嫁接和另外三种离散模型训练方法的训练损失，以及使用改进前后的逻辑激活函数的训练损失。

实例展示

权重分布

图 6 展示的是不同正则项系数所对应的 RRL 线性层权重（规则重要度）的分布情况。当正则项系数比较小时，RRL 产生的规则比较复杂，数量较多。但从分布可以看出，大多数是权重绝对值较小的规则。因此，可以先去理解权重值较大的重要规则，当对模型整体和数据有了更好的认识后，再去理解权重较小的规则。而当正则项系数较大时，RRL 整体复杂度较低，则可以直接理解模型整体。

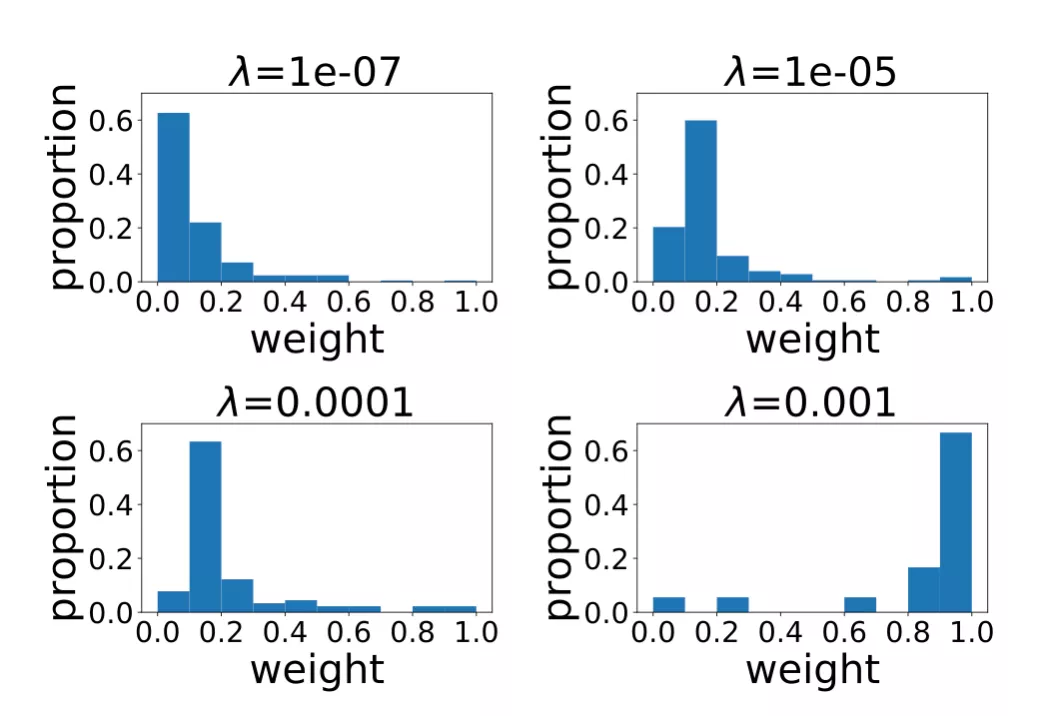
图 6：不同正则项系数所对应的线性层权重分布。

具体规则

图 7 为 bank-marketing 数据集所学到的部分规则，这些规则被用于预测用户是否会在电话销售中接受银行的贷款。可以从这些规则中直观看出哪些用户状态以及公司行为会对销售结果产生影响，例如中年已婚的低存款用户更可能接受贷款。银行可以根据这些可解释的规则来调整自己的营销策略，以增加销量。

虽然 RRL 并非专门设计用于图像分类任务，但得益于其较好的可扩展性，RRL 仍可以通过可视化的方式为图像分类任务提供直观的解释。图 8 是对 fashion-mnist 图像数据集上 RRL 所学到的规则的可视化。从中可以直观地总结出模型的决策模式，例如通过袖子长短区分 T 恤和套头衫。

图 7：RRL 在 bank-marketing 数据集上学到的部分规则。

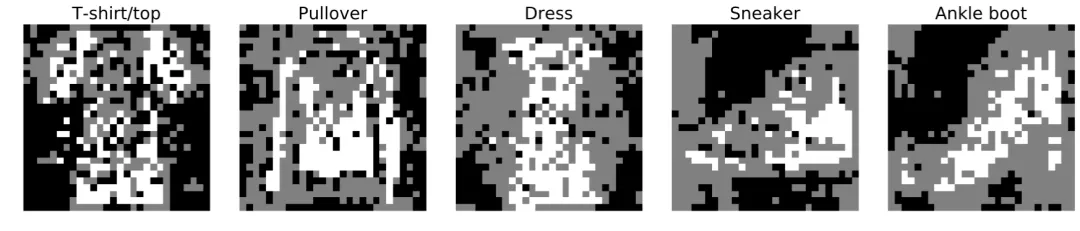
图 8：RRL 在 fashion-mnist 图像数据集上学到的规则的可视化。

总结

论文提出了一种新的可扩展分类器，规则表征学习器（RRL）。RRL 能够通过自动学习可解释的非模糊规则进行数据表征和分类。得益于自身的模型结构设计、梯度嫁接法以及改进版逻辑激活函数的使用，RRL 不仅有着较强的可扩展性，还能在模型复杂度较低的前提下获得较好的分类效果。

RRL 的提出，不仅使得可解释规则模型能够适用于更大的数据规模和更广的应用场景，还为从业人员提供了一个更好的在模型复杂度和分类效果之间权衡的方式。在未来工作中，把 RRL 拓展到非结构化数据上，如图像和文本等，从而提升此类数据模型的可解释性。