本文转载自微信公众号「志斌的python笔记」,作者安可 。转载本文请联系志斌的python笔记公众号。
大家好,我是志斌~
志斌现在手头上有一个国际象棋的残局,它是黑方只剩下一个王,白方剩一个兵和一个王。现在志斌已知它有两种可能的结局,即白方将死黑方获胜,或者和棋。
那么结局到底是什么呢?接下来让我们用深度学习的人工神经网络算法,来给大家一个答案~
一.规则介绍
在进行程序编译之前,我们需要先简单的了解一下国际象棋的下棋规则,规则如下:
棋盘大小为8*8,各有黑色和白色棋子16个,分别是王:1个,后:1个,车:2个,象:2个,马:2个,兵:8个。
兵:只能向前直走(不能后退,这点和中国象棋类似),每次行棋只能走一格。但是,国际象棋的兵走第一步时,可以走一格或走两格。兵的吃子方法与行棋方向不一样,它是直走斜吃,即如果兵的前斜进一格内有对方棋子,就可以吃掉它,从而占据该格位置。
王:则是横、直、斜都可以走,但每次限走一步。不过,和中国象棋相比,王是不可以送吃的,即任何被敌方控制的格子,己方王都不能走进去。否则,算“送王”犯规。累计三次犯规就要判负。
胜负:当吃掉对方的最高统帅 王 时则胜,当逼对方不能走棋了,则算和。
二.解决方法
1读取训练集
对krkopt.data训练集进行读取,代码如下:
- with open('krkopt.data','r') as f:
- lines = f.readlines()
- data = np.zeros((28056,6),dtype=float)
- label = np.zeros((28056,2),dtype=float)
读取结果展示:
上面每一行数据都是一个训练样本,我们以第一行的数据为例来进行分析,如下图:
a1,b3,c2给出了三个棋子的坐标,黑方的王在如图a1的位置,白方的王在如图b3的位置,白方的兵在如图c2 的位置。这时黑方的王处于无路可走的状态,是和棋,因此,最后draw意为和棋。假设数据中最后标签为six,意为白方最多走6步可将死黑方。
2开始训练
首先安装训练所需要调用的Python库,
- pip install numpy
- pip install sklearn
- pip install matplotlib
然后将整个数据集分为三份,代码如下:
- ratioTraining = 0.4 #训练数据集40%:利用训练数据集调整神经网路的参数
- ratioValidation = 0.1 #验证数据集10%:用于验证调整是好是坏,从而决定程序是否退出
- ratioTesting = 0.5 #测试数据集50%:训练结束后,用于总体测出神经网络的训练效果
接下来使用Scikit-learn中的Scaler类,采用减掉均值除以方差的方法对标准进行归一化,代码如下:
- scaler.transform(xTraining)
- scaler.transform(xTexting)
- scaler.transform(xValidation)
创建神经网络,代码如下:
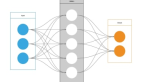
其中:layer=[6, 20, 20, 20, 2]输入是6个维度,输出是2个维度,共3层神经网络,每层20个神经元
- active_function='relu'神经网络的激活函数
- learning_rate=0.01学习率α
- batch_normalization=1归一化操作
- objective_function='Cross Entropy'目标函数
训练开始后,我们发现COST损失函数是在持续下降,同时识别率Accuracy,在慢慢上升,无限接近于1。
代码如下:
经过上面的分析,我们发现白棋胜的几率很高,几乎接近1了。
三.小结
1. 本文利用一局国际象棋残局胜负为例,带大家实操人工神经网络算法,希望大家回去多多练习。
2. 本文仅供学习参考,不做它用。
专栏作者:安可,一名在读研究生,研究领域为强化学习,多智能体协同。喜欢钻研,热爱学习,乐于分享,最重要的还是一位漂亮小姐姐哦~