近来机器学习模型呈现出一种向大模型发展的趋势,模型参数越来越多,但依然具有很好的泛化性能。一些研究者认为泛化性能得益于随机梯度下降算法(SGD)所带来的随机噪声。但最近一篇 ICLR 2022 的投稿《Stochastic Training is Not Necessary for Generalization》通过大量实验证实全批量的梯度下降算法(GD)可以达到与 SGD 不相上下的测试准确率,且随机噪声所带来的隐式正则化效应可以由显式的正则化替代。

论文地址:https://arxiv.org/pdf/2109.14119.pdf
该论文随即在社区内引发了一些讨论,有人质疑论文的含金量,觉得个例不具代表性:
也有人表示这篇论文就像一篇调查报告,提出的观点和证明过程并无新意:

图源:知乎用户 @Summer Clover
虽然内容有些争议,但从标题上看,这篇论文应该包含大量论证,下面我们就来看下论文的具体内容。
随机训练对泛化并不是必需的
随机梯度下降算法 (SGD) 是深度神经网络优化的支柱,至少可以追溯 1998 年 LeCun 等人的研究。随机梯度下降算法成功的一个核心原因是它对大型数据集的高效——损失函数梯度的嘈杂估计通常足以改进神经网络的参数,并且在整个训练集上可以比全梯度更快地进行计算。
人们普遍认为,随机梯度下降 (SGD) 的隐式正则化是神经网络泛化性能的基础。然而该研究证明非随机全批量训练可以在 CIFAR-10 上实现与 SGD 相当的强大性能。基于此,该研究使用调整后的超参数,并表明 SGD 的隐式正则化可以完全被显式正则化取代。研究者认为这说明:严重依赖随机采样来解释泛化的理论是不完整的,因为在没有随机采样的情况下仍然可以得到很好的泛化性能。并进一步说明:深度学习可以在没有随机性的情况下取得成功。此外,研究者还表示,全批量训练存在感知难度主要是因为:优化特性和机器学习社区为小批量训练调整优化器和超参数所花费的时间和精力不成比例。
具有随机数据增强的全批量 GD
SGD 相对于 GD 有两个主要优势:首先,SGD 的优化过程在稳定性和超出临界批量大小的收敛速度方面表现出质的飞跃。其次,有研究表明,小批量上由步长较大的 SGD 引起的隐式偏差可以用等式(5)和等式(7)中导出的显式正则化代替。
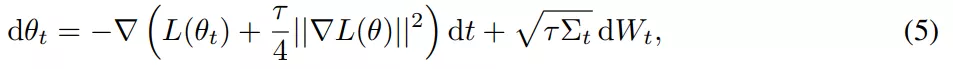
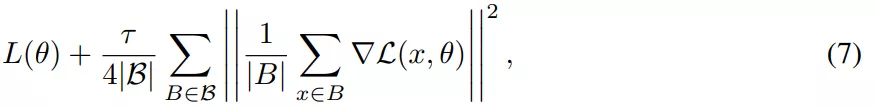
该研究对假设进行了实证研究,试图建立训练,使得在没有来自小批量的梯度噪声的情况下也能实现强泛化,核心目标是实现全批量性能。因此该研究在 CIFAR-10 上训练了一个用于图像分类的 ResNet 模型进行实验。
对于基线 SGD ,该研究使用随机梯度下降进行训练、批大小为 128 、 Nesterov 动量为 0.9、权重衰减为 0.0005。
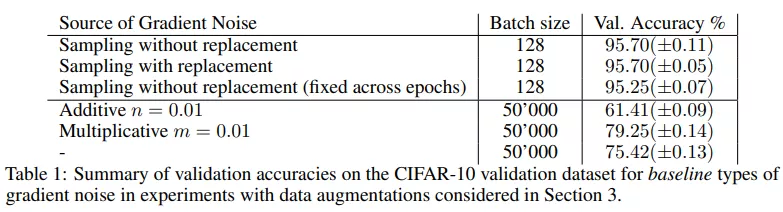
小批量 SGD 的验证准确率达到了 95.70%(±0.05)。小批量 SGD 提供了一个强大的基线,在很大程度上是独立于小批量处理的。如下表 1 所示,在有替换采样时也达到相同的准确率 95.70%。在这两种情况下,随机小批量处理引起的梯度噪声都会导致很强的泛化。
然后,该研究将同样的设置用于全批量梯度下降。用全批量替换小批量,并累积所有小批量梯度。为了排除批归一化带来的影响,该研究仍然在批大小为 128 的情况下计算批归一化,在整个训练过程中将数据点分配给保持固定的一些块,使得批归一化不会引入随机性。与其他大批量训练的研究一致,在这些设置下应用全批量梯度下降的验证准确率仅为 75.42%(±00.13),SGD 和 GD 之间的准确率差距约为 20%。
该研究注意到,通过注入简单形式的梯度噪声不容易弥补这一差距,如下表 1 所示。接下来的实验该研究努力缩小了全批量和小批量训练之间的差距。
由于全批量训练不稳定,因此该研究在超过 400 step(每一个 step 是一个 epoch)的情况下将学习率从 0.0 提升到 0.4 以保持稳定,然后在 3000 step 的情况下通过余弦退火衰减到 0.1。
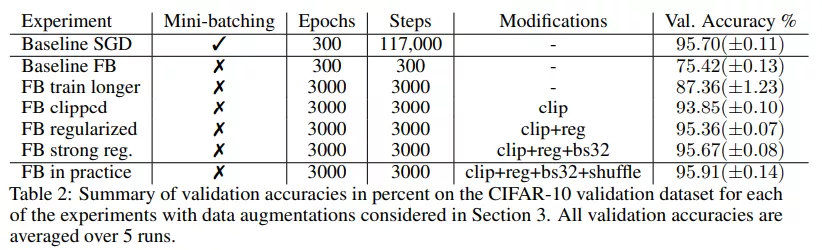
实验表明在对训练设置进行了一些修改后,全批量梯度下降性能提高到了 87.36%(±1.23),比基线提高了 12%,但仍与 SGD 的性能相去甚远。表 2 中总结了验证分数:
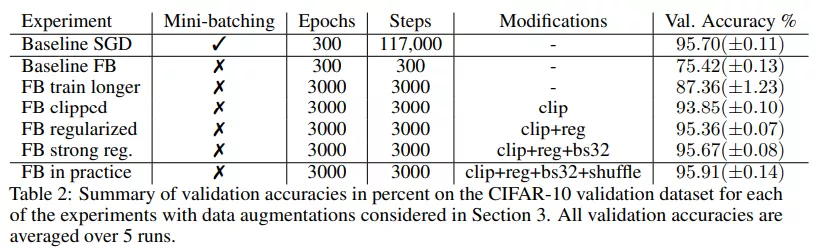
该研究用显式正则化来弥补这种差距,并再次增加了初始学习率。在第 400 次迭代时将学习率增加到 0.8,然后在 3000 step 内衰减到 0.2。在没有正则化因子的情况下,使用该学习率和 clipping 操作进行训练,准确率为 93.75%(±0.13)。当加入正则化因子时,增大学习率的方法显著提高了性能,最终与 SGD 性能相当。
总体而言,该研究发现经过所有修改后,全批量(带有随机数据增强)和 SGD 的性能相当,验证准确率显著超过 95%。
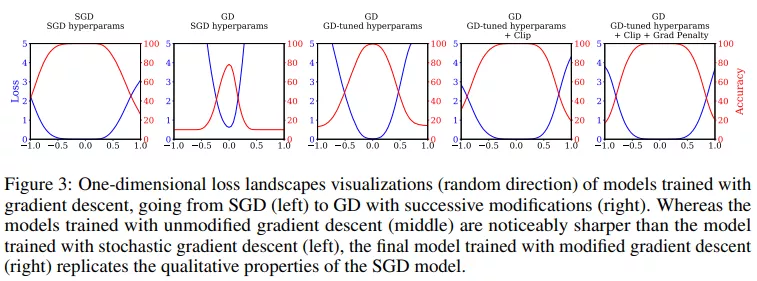
该研究还评估了一系列具有完全相同超参数的视觉模型。ResNet-50、ResNet-152 和 DenseNet-121 的结果见表 3,该研究发现所提方法也同样适用于这些模型。
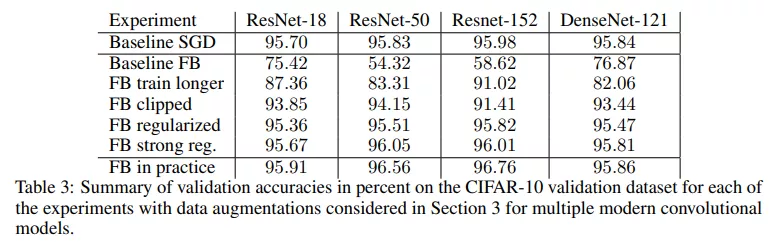
非随机设置下的全批量梯度下降
如果全批量实验能够捕捉小批量 SGD 的影响,那么随机数据增强又会给梯度噪声带来什么影响?研究者又进行了以下实验。
无数据增强:如果不使用任何数据增强方法,并且重复之前的实验,那么经过 clipping 和正则化的 GD 验证准确率为 89.17%,显著优于默认超参数的 SGD(84.32%(±1.12)),并且与新调整超参数的 SGD(90.07%(±0.48)) 性能相当,如下表 4 所示。

为了相同的设置下分析 GD 和 SGD,探究数据增强(不含随机性)的影响,该研究使用固定增强的 CIFAR-10 数据集替换随机数据增强,即在训练前为每个数据点采样 N 个随机数据进行数据增强。这些样本在训练期间保持固定,也不会被重新采样,从而产生放大 N 倍的 CIFAR-10 数据集。
最后,该研究得出结论:在没有小批量、shuffling 以及数据增强产生的梯度噪声后,模型也完全可以在没有随机性的情况下达到 95% 以上的验证准确率。这表明,通过数据增强引入的噪声可能不会影响泛化,并且也不是泛化所必需的。
引发讨论
这篇论文在社区内引发了大家的讨论,有人从实验的角度分析了一下论文的价值。
该论文把 ResNet18 用 SGD 在 CIFAR-10 训练 300 个 epoch 作为基线,并在结果部分展示了每一个 trick 分别提升了多少准确率。
但是这几个 trick 太常见了,反而让人质疑真的如此有效吗?有网友指出「train longer」这个 trick 应该只在 CIFAR-10 上这么有效,而 gradient clipping 在其他数据集上甚至可能无效。

图源:知乎用户 @Summer Clover
看来论文中的改进可能是个例,难以代表一般情况。不过,他也在评论中指出 SGD 近似正则化项
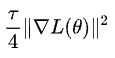
是个很有效的 trick,具备很好的理论基础,但是计算成本可能会翻倍:

图源:知乎用户 @Summer Clover
还有网友指出,这篇论文的研究结果实际用途很有限,因为全批量设置的成本太高了,不是普通开发者负担得起的。相比之下,SGD 训练鲁棒性强,泛化性更好,也更省一次迭代的计算资源。
看来该论文进行了一些理论和实验验证,但正如网友提议的:能否在其他数据集上进行更多的实验来验证其结论?

对此,你怎么看?



























