长久以来一个观点就是在测试集上表现更好的模型,泛化性一定更好,但事实真是这样吗?LeCun团队最近发了一篇论文,用实验证明了在高维空间下,测试集和训练集没有关系,模型做的一直只有外推没有内插,也就是说训练集下的模型和测试集表现没关系!如此一来,刷榜岂不是毫无意义?
内插(interpolation)和外推(extrapolation)是机器学习、函数近似(function approximation)中两个重要的概念。
在机器学习中,当一个测试样本的输入处于训练集输入范围时,模型预测过程称为「内插」,而落在范围外时,称为「外推」。
一直以来深度学习的研究都依赖于两个概念:
- 最先进的算法之所以工作得这么好,是因为它们能够正确地内插训练数据;
- 在任务和数据集中只有内插,而没有外推。
但图领奖得主Yann LeCun团队在arxiv挂了一篇论文公开质疑这两个概念是错误的!

他们在论文中表示,从理论上和经验上来说,无论是合成数据还是真实数据,几乎可以肯定的是无论数据流形(data manifold)的基本本征维数(intrinstic dimension)如何,内插都不会出现在高维空间(>100)中。
本征维度即在降维或者压缩数据过程中,为了让你的数据特征最大程度的保持,你最低限度需要保留哪些features,它同时也告诉了我们可以把数据压缩到什么样的程度,所以你需要了解哪些 feature 对你的数据集影响是最大的。
考虑到当前计算能力可以承载的实际数据量,新观察到的样本极不可能位于该数据集的convex hull中。因此,他们得出了两个结论:
- 目前使用和研究的模型基本都是外推的了;
- 鉴于这些模型所实现的超越人类的性能,外推机制也不一定非要避免,但这也不是泛化性能的指标。
文中研究的第一阶段主要包括理解环境维度(即数据所在空间的维度)的作用,还包括基本数据流形内在维度(即数据最小表示所需的变量数量)的作用,以及包含所有数据流形的最小仿射子空间的维数。
可能有人认为像图像这样的数据可能位于低维流形上,因此从直觉和经验上认为无论高维环境空间如何,内插都会发生。但这种直觉会产生误导,事实上,即使在具有一维流形的极端情况下,底层流形维度也不会变化。
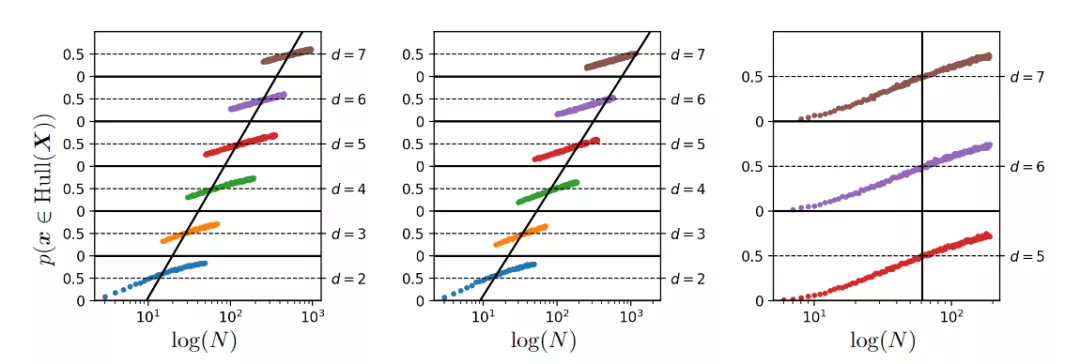
在描述新样本处于内插区域的概率演变时,上图给出了在对数尺度上看到的不断增加的数据集大小,以及基于对500000次试验的蒙特卡罗估计的各种环境空间维度(d),左侧图为从高斯密度N(0, Id)中采样数据,中间图从具有1的本征维数的非线性连续流形采样数据,右图从高斯密度恒定维数4的仿射子空间中采样数据,而环境维数增加。
从这些数字可以清楚地看出,为了保持内插区域的恒定概率,不管潜在的内在流形维度训练集的大小必须随d呈指数增长,其中d是包含整个数据流形的最低维仿射子空间的维数。
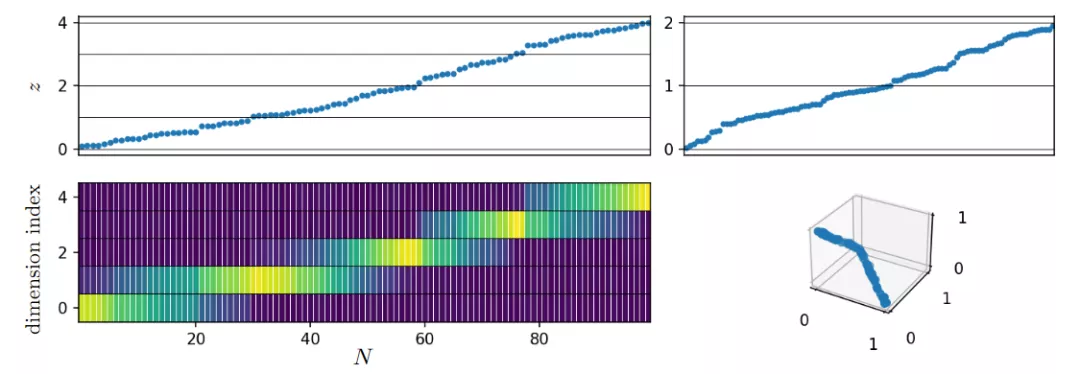
在所有情况下,该数据集的本征维度均为1,流形是连续的、非线性的、分段光滑的,对应于单纯形的遍历。
因此可以得出结论,为了增加处于内插区域的概率,应该控制d, 而不是控制流形基础维度和环境空间维度。
在研究像素空间中的测试集外推时,研究人员首先研究了MNIST、CIFAR和Imagenet序列集中处于插值状态的测试集的比例。
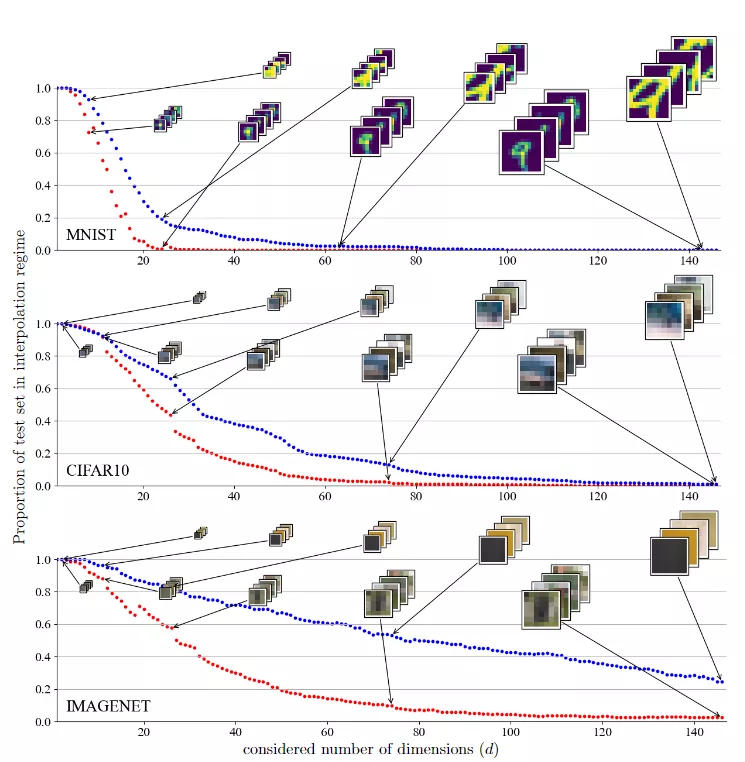
为了掌握数据维度的影响,使用从两种策略获得的不同数量的维度来计算该比例。第一种策略只从图像的中心保留一定数量的维度,它的优点是保留流形几何体,同时只考虑有限的维数;第二种策略对图像进行平滑和子采样,它的优点是能够保留流形的整体几何体,同时删除高频结构(图像细节)并压缩较少维数的信息。
在这两种情况下都看到,尽管自然图像具有数据流形几何结构,但相对于数据维度d,在内插区域中查找样本还是非常困难。
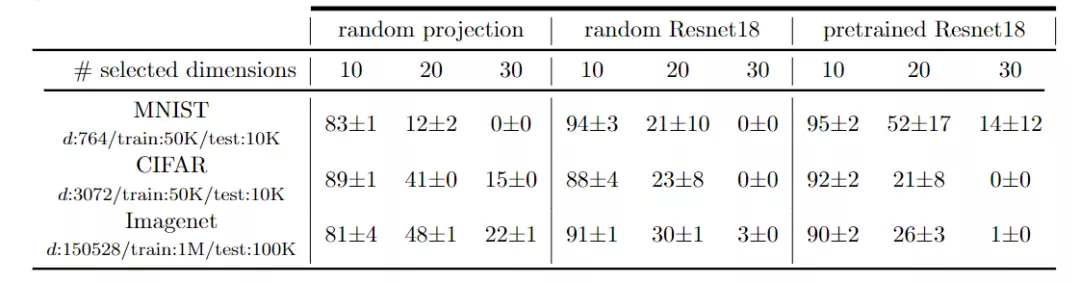
在降维空间中研究测试集外推时,一组实验使用非线性或线性降维技术来可视化高维数据集。为了明确地了解所用的降维技术是否保留了内插或外推信息时,研究人员创建了一个数据,该数据由d=8,12的d维超立方体的2d顶点组成。
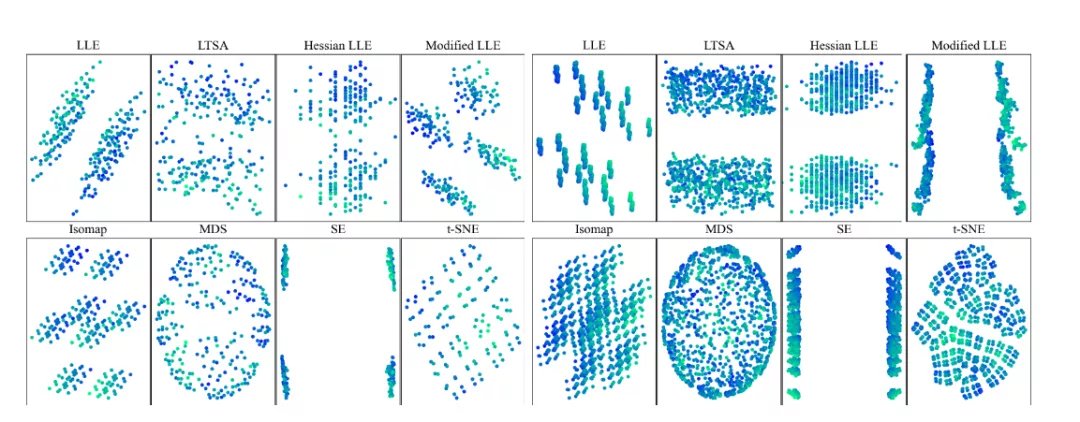
这些数据集具有特定性,即任何样本相对于其他样本都处于外推状态。并且使用8种不同的常用降维技术对这些顶点进行二维表示。可以观察到降维方法会丢失内插/外推信息,并导致明显偏向插值的视觉误解。
内插和外推提供了一种关于给定数据集的新样本位置的直观几何特征,这些术语通常被用作几何代理来预测模型在看不见的样本上的性能。从以往的经验来看似乎已经下了定论,即模型的泛化性能取决于模型的插值方式。这篇文章通过实验证明了这个错误观念。
并且研究人员特别反对使用内插和外推作为泛化性能的指标,从现有的理论结果和彻底的实验中证明,为了保持新样本的插值,数据集大小应该相对于数据维度呈指数增长。简而言之,模型在训练集内的行为几乎不会影响该模型的泛化性能,因为新样本几乎肯定位于该凸包(convex)之外。
无论是考虑原始数据空间还是嵌入,这一观察结果都是成立的。所以研究人员认为,这些观察为构建更适合的内插和外推几何定义打开了大门,这些定义与泛化性能相一致,特别是在高维数据的情况下































