我们经常会遇到这样一个问题:
多个元素之间有很多种排列组合,让我们选出满足某个条件的最好的那个。
比如说:
- 一个字符串可以有 n 种子串,让我们从中选出最长的回文串。(回文串是指 abccba 这种反过来和原字符串相等的字符串)
- n 个物品之间有很多种组合方案,让我们选出满足满足重量小于某个值的最大价值的组合方案
这些问题我们最容易想到的思路就是枚举出所有的情况,然后做下验证和比较。
比如,第一个问题:
我们可以枚举出所有的子串,然后判断是否是回文串,记录下最长的那个。
第二个问题:
可以枚举出所有的组合方案,然后验证下是否满足重量小于某个值,记录下满足条件的价值最大的方案。
这种把所有的排列组合枚举出来,然后依次验证和比较的思路是最容易想到的,很多问题我们都是这样解决。
但是这样做一些简单场景的业务需求还行,要是数据规模一上去,立马 gg。
为什么呢?
第一个问题的解决方案,要枚举所有的子串,需要枚举所有起始点和终止点坐标的坐标,然后再判断是否是回文串。
这需要 2 重循环来枚举子串, 1 重循环来判断是否回文并和最大值比较。
也就是 O(n^3) 的复杂度。
而第二个问题的解决方案,需要枚举所有的组合,每一个物品都有选与不选两种情况,需要递归 n 次来计算所有的情况,也就是一共有 2^n 种情况,枚举出的组合方式还要计算下这 m 个物品的价值的和。
也就是 O(2^n * m) 的复杂度。
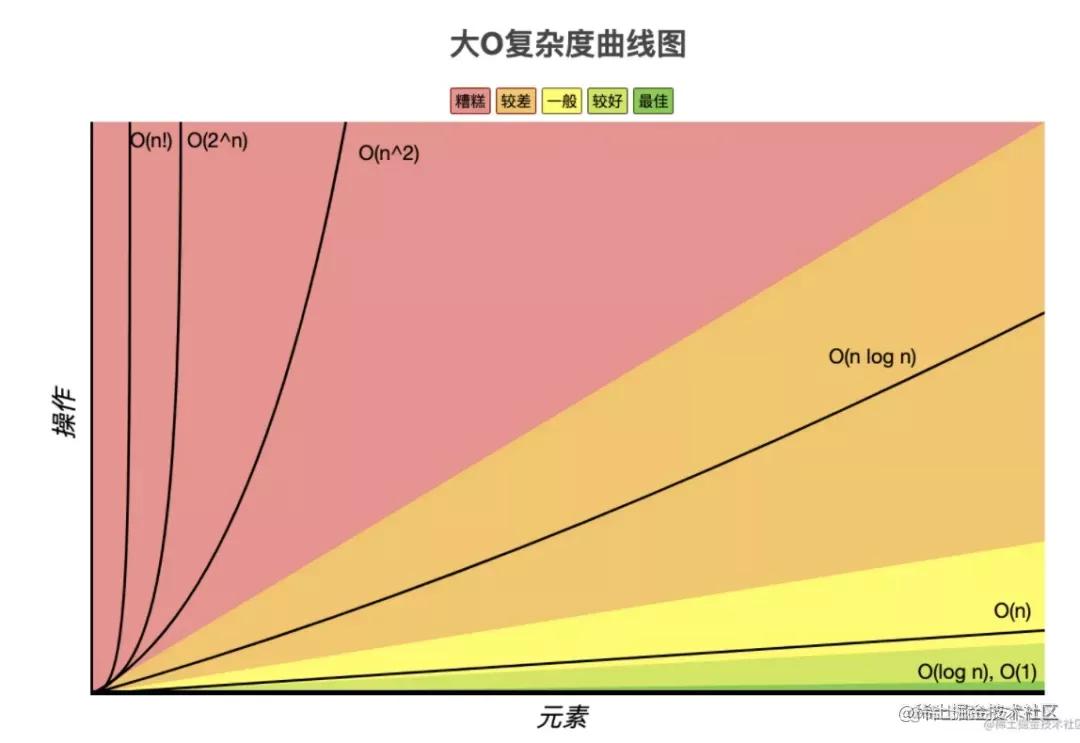
这种方案来解决业务问题可以么?可以,其实很多情况下我们都用这种朴素的容易想到的思路来解决,但是数据规模一上去,这些方案就都不行了。原因见下图:
数据规模比较大的时候,就要换时间复杂度更低的算法了。
怎么把时间复杂度降下来呢?
我们现在是每一个都枚举出来然后单独判断的:
每一种情况都要单独这样来一遍,所以组合越多,复杂度越高。
能不能找到各种组合之间的规律呢,比如可以从一种情况推出另一种情况,那不就不用每次都验证一遍了么?
比如回文串那个问题,如果我们知道了 i 和 j 是回文串,那如果前后两个字符如果相等的话, i-1 到 j+1 不也是回文串么?
所以就可以找到这样的推导关系:
- if (str[i] === str[j] && isHuiwen[i+1][j-1]) {
- isHuiwen[i][j] = true;
- }
有了这个推导关系之后有啥变化呢?我们根本不用枚举出每种情况再单独验证了,从一个初始的情况推导出后面所有的情况不就行了么?
直接从结果来推导,这样复杂度一下子从 O(n^3) 降低到了 O(n)。
这种找各种情况之间规律,然后从初始状态根据状态转移方程推导出所有状态的算法就叫做动态规划。
背包问题如果能找到结果之间的推导关系,也就不用枚举 + 验证了,可以直接推出来。
我们试着找一下:
我们关心的是 i 件物品,可用容量为 j 的时候,最大价值是多少。
那么第 i 件物品和 i-1 件物品的关系是什么呢?就是装与不装。
如果可用容量 j 小于第 i 件物品的重量 w[i],那么装不下。
也就是
- if (j < w[i]) {
- maxValue[i][j] = maxValue[i -1][j]
- }
如果可用容量 j 大于等于第 i 件物品的重量 w[i],那么就能装下。
能装下就可以分为装与不装两种情况,取大的那个即可:
- if (j >= w[i]) {
- maxValue[i][j] = Math.max(maxValue[i][j - w[i]] + val[i], maxValue[i-1][j])
- }
这就是第 i 件物品与第 i-1 件物品的关系:
- if (j < w[i]) {
- maxValue[i][j] = maxValue[i -1][j]
- } else {
- maxValue[i][j] = Math.max(maxValue[i][j - w[i]] + val[i], maxValue[i-1][j])
- }
这个状态转移方程列出来了之后,就能从初始状态推导出所有的状态,然后取其中满足容量 w 的 n 件物品的最大价值。
复杂度从 O(2^n * m) 降低到了 O(n * m)。
总结
当遇到从多种组合中取满足需求的那种组合的问题时,一般的思路就是枚举 + 验证,但是这种思路算法复杂度很高,性能很差。
如果能找到各种组合的情况之间的推导关系,就可以直接推导出来,比如 i 到 j 的回文串和 i-1 到 j+1 的回文串之间的关系,比如 i 个物品容量为 j 的最大价值和 i-1 个物品容量为 j 的关系。
这种思路叫做动态规划算法。
动态规划的难点在于找 i 和 i-1 的推导关系,也就是列出状态转移方程。
一旦理清了状态转移方程,也就是各组合的结果(状态)之间的推导关系,就可以从初始状态把后续所有状态推导出来。能够极大的降低朴素算法的复杂度,提升几个数量级的性能。