介绍
最近经常看到有人发一个Go实现的分布式事务管理器dtm,看到star增的挺猛的,索性看看代码实现,毕竟工作中部分场景也用的上。
在写源码分析之前,我们先来简单入门一下分布式理论。
CAP
分布式系统中很大的一个难点在于各个节点之间的状态如何同步,CAP就是分布式系统领域一条已经被证明的定律。
其中各个字母的含义如下:
- Consistency(一致性)
- Availability(可用性)
- Partition tolerance(分区容忍性)
我们先用一个简单的例子来说明。
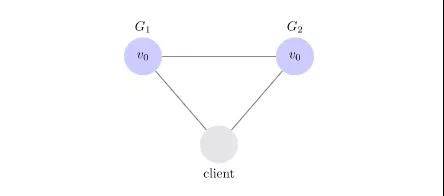
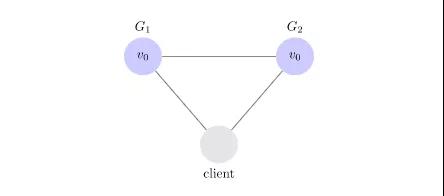
假设我们的系统是由两个服务组成的:G1和G2。
G1和G2维护了同一条记录V0。外部客户端(Client)可以调用任意一个服务。
当一个客户端对任意一个服务发起读|写请求,那么被请求的那个服务器根据客户端的请求,处理、响应结果。
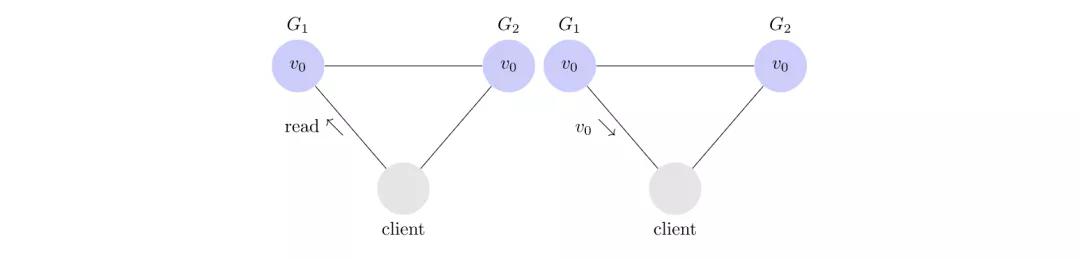
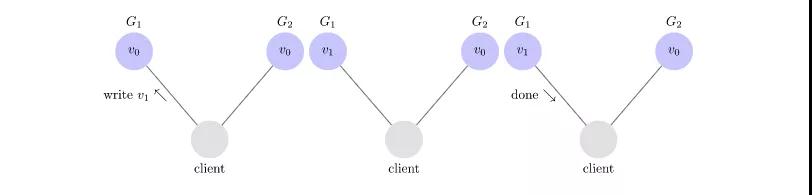
比如客户端向G1发起一个读操作,客户端G1响应请求。
又比如客户端向G1发起一个写操作,把V0修改成V1。
到这里,我们建立了这样一个系统。接下来看看系统的一致性、可用性和分区容忍性意味着什么。
Consistency(一致性)
这个一致性和事务中ACID中的C还是有区别的。事务中的C更多是指在事务开始之前和事务结束以后,数据库的完整性没有被破坏。这里的完整性包括一些外键约束、键的唯一性等。
而分布式事务中的C指的是,写操作之后的读操作,必须返回该值,这就等同于所有节点访问的是同一份最新数据的副本。
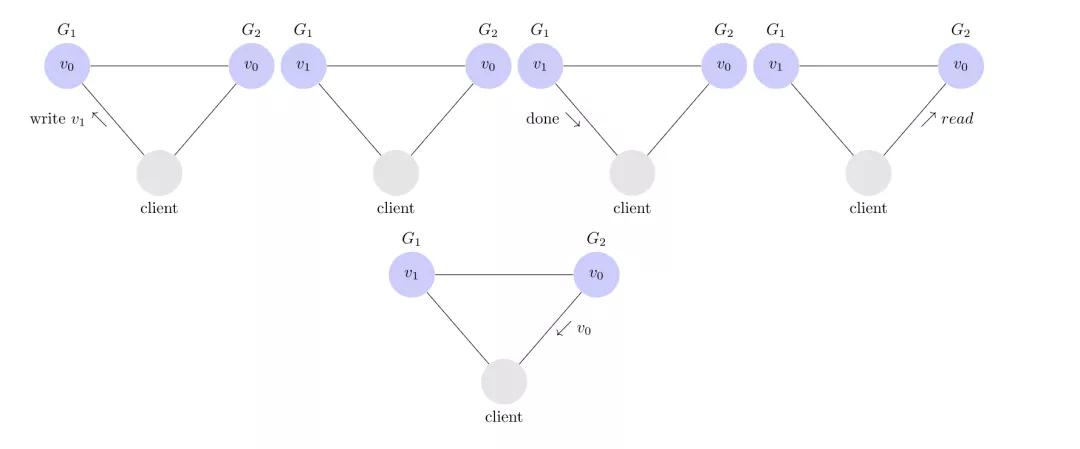
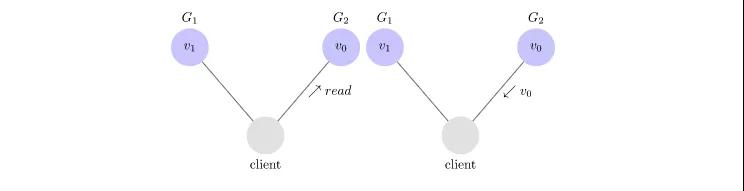
下面是一个非一致性的例子。
客户端成功请求G1服务器写V1。假设当前服务G1和G2不能互通(网络分区),导致G1数据不能同步到G2,此时客户端从G2读取数据,依旧返回V0。
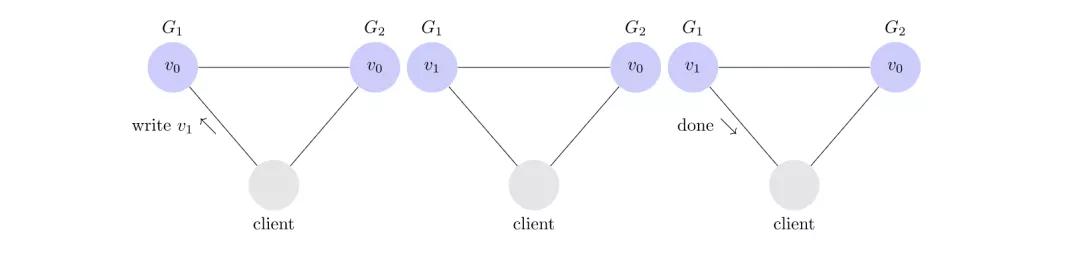
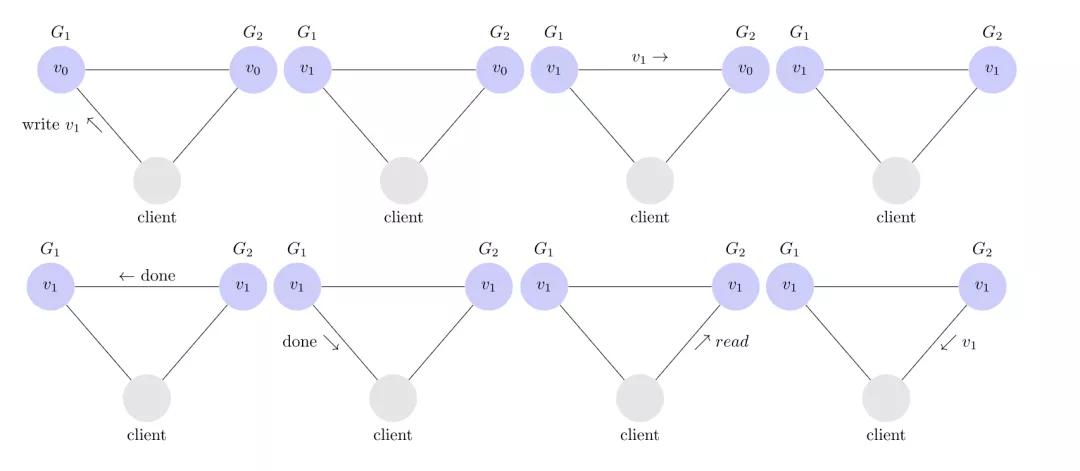
来看一个满足一致性的例子。
在这个系统中,G1收到客户端写V1的操作,G1在修改自身数据的同时,会把V1数据同步到G2。G1在收到G2的响应后,才向客户端响应结果。这样,之后无论客户端从哪个节点读取数据,都能获取到V1值。
Availability(可用性)
可用性指的是系统中非故障节点接收到的每一个请求都必须响应。
在一个可用的系统中,如果客户端向服务器发送一个请求,那么服务器必须响应客户端每一个请求,不允许忽略客户端请求。
Partition Tolerance(分区容忍性)
什么分区?
网络分区。
网络分区咋么理解?
假设有两台服务器A和B,本来他们两是正常通信的,不知道啥原因,他们之间的网络链接断开,导致无法正常通信。此时本来在同一个网络的AB,发生了网络分区。变成了A所在的A网络和B所在的B网络。这就是网络分区。
容忍性是指什么?
当一个服务的多台服务器发生上述网络分区的时候,系统依旧能正常提供服务。
对CAP的误解
网上很多文章都是这么说的:
一个分布式系统最多只能同时满足一致性(Consistency)、可用性(Availability)和分区容错性(Partition tolerance)这三项中的两项,这被称为CAP定律。
似乎CAP被解释成一种三选二的定律。
看到一篇文章CAP Twelve Years Later: How the "Rules" Have Changed[1]有一段CAP的完整表述:
The CAP theorem asserts that any net-worked shared-data system can have only two of three desirable properties。
按照表述,发现网上这句话存在一定的误导性。
CAP定律的前提是P(网络分区)发生后,才会有CA的选择。
当P发生的时候,而我们的系统直接不服务了,那就不存在选择什么CA了。
因此CAP的正常理解应该是:当P(网络分区)发生的时候,如果我们要继续提供服务,那么C(一致性)和A(可用性)只能2选1了。
Consistency和Availability的矛盾
为什么当P发生时,CA只能二选一?
还是之前那个简单的例子。
假设此时G1和G2发生了网络分区。
接下来我们的客户端请求G1写V1数据。由于分区,G1不能同步数据到G2。
如果我们保证G2的可用性,那么当客户端请求G2数据的时候,G2能正常响应V0数据,但是数据和G1不一致,无法保证一致性。
如果我们保证G2的一致性,那么在G1写操作的时候,就必须锁定G2的读写操作,那么此时G2就处于不可用状态,无法保证其可用性。
因此,Consistency和Availability存在矛盾。
参考
https://www.infoq.com/articles/cap-twelve-years-later-how-the-rules-have-changed/
https://mwhittaker.github.io/blog/an_illustrated_proof_of_the_cap_theorem/
https://www.zhihu.com/question/64778723