本文转载自微信公众号「码工小熊」,作者小熊妹 。转载本文请联系码工小熊公众号。
大家好,我是爱学习的小xiong熊妹。
总有小伙伴想看分析模型,我们就从最简单的回归分析模型讲起。回归分析是所有分析模型里最浅显,最容易懂的,并且回归分析有很多变化形态,能适用于很多问题场景。今天就一起来看一下。
一、为什么叫回归?
回归翻译自:regression,最初是统计学家们,关注到:孩子的身高总会向平均身高靠近,即使父母都很高,孩子也不会无限长高下去。从这些研究里,总结出回归分析方法(regression,还有一个意思是:退化,可以说很形象了)。
所以,这里的“回归”只是一个习惯称呼,和业务部门口中的“回归初心”“回归原点”一毛钱关系都没有!在讨论问题的时候,业务部门最喜欢扯“回归”,做数据的小伙伴们,千万别被绕进去了!!!
二、回归模型有什么用?
回归模型是用来做:预测的。
在数据分析里,预测分两种:
- 连续型预测:比如预计销售额是3550万,预测客户15万,预测结果是一个连续型数字。
- 分类预测:比如预计用户接电话/不接电话,预计新品上市后是A级/B级/C级,预测结果不是一个连续型数字,而是一个分类结果。
大部分回归分析模型都是连续型预测(逻辑回归除外)。今天就从最简单的,只有一个变量的简单线性回归分析讲起。
三、如何进行回归分析
做回归分析有五步:
- 第一步:确认是否是预测问题
- 第二步:确认要预测的因变量,影响预测结果的自变量
- 第三步:收集数据,检验数据间关系
- 第四步:计算模型,检验结果
- 第五步:进行预测
看个具体问题场景:某公司在新品上市前,会提前进行宣传,并进行预约。虽然最终上市以后,并非只有预约用户买,但是如果能通过预约人数,预测销售情况,就能提前预判商品会不会受欢迎,从而把控库存情况。具体数据如下表。
拿到问题后,一步步来:
第一步:该场景需要的是预测,要预测的是销售额,是一个连续型变量。
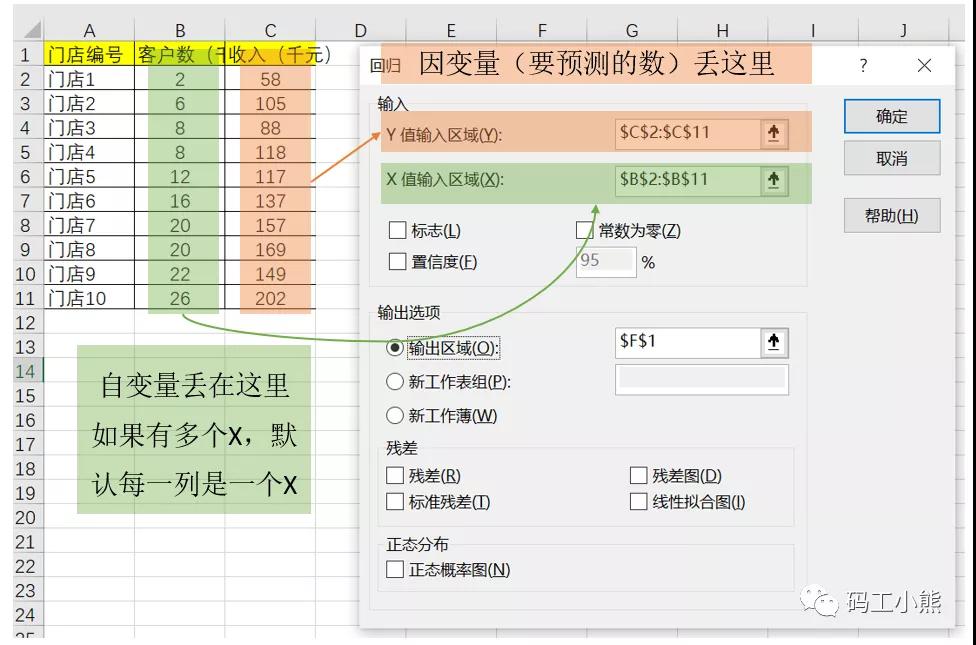
第二步:确认因变量,自变量。该问题中:
因变量(要预测的):销售额
自变量(影响预测结果的):预约人数
没有其他变量了。
拿到数据后,可初步判断两个指标是否有关系,是何种关系,从而选择合适的模型。判断关系,最简单快捷的方法就是:散点图。因此拿到数据以后,可以先做散点图。如上图所示,因变量和自变量之间看起来是有明显线性关系的,因此可以用线性回归来做。
第三步:收集数据,题目已帮忙收集好了,进入下一步。
第四步:进行计算。简单的线性回归,用excel→数据分析→回归即可计算(如下图)
至于模型解读,略为复杂,我们慢慢看哦
四、模型计算与解读
回归分析的模型解读略显复杂,并且包含了大量假设检验的知识,这里先不探讨其复杂原理,给个最简单的判断原则,小伙伴们抄起来能用即可。
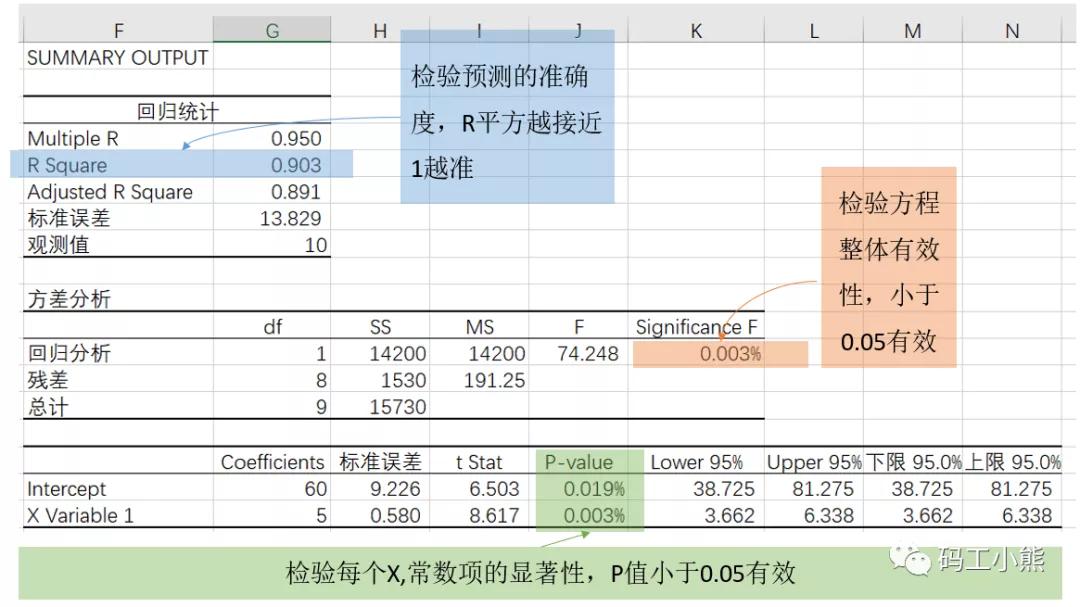
模型解读,分为三个部分:
- 模型本身预测准不准。主要看R平方(如下图蓝色)
- 模型整体是否有效。主要看F检验的结果(如下图橙色)
- 模型里,每个因变量的检验结果(如下图绿色)
从上图可以看出,本次建模的三个检验结果全部通过,表明模型可用。
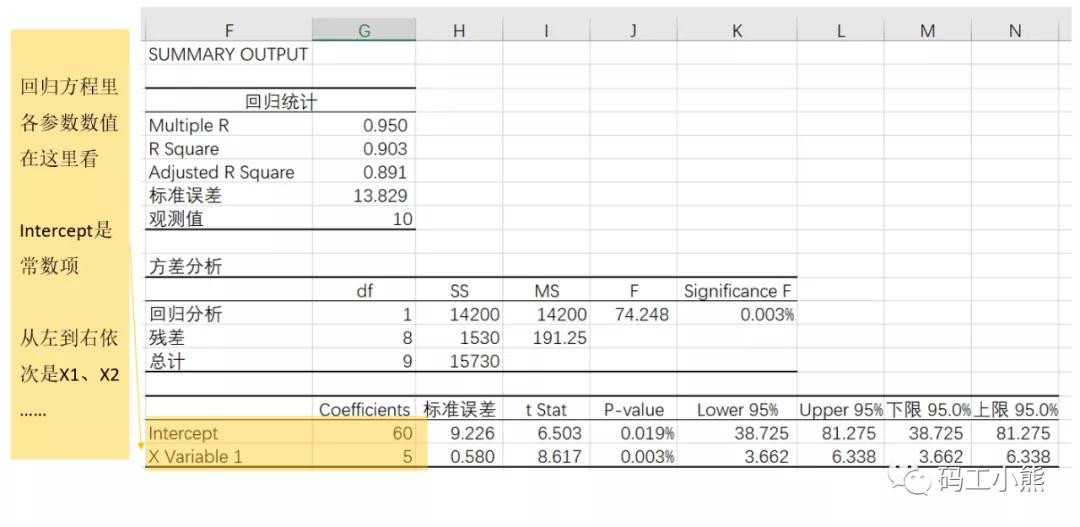
这次建模只有一个自变量+一个常数项,因此最终模型就是y=60+5x。常数项和自变量的数值,参见下图黄色部分:
五、回归分析模型应用
有了回归模型,我们就能预测未来情况啦。比如有一款新品,预约人数为4.5万人,则可以代入模型,预测销量为60+5*4.5=82.5万,商品部门就能据此备货了。
六、回归分析局限性
没有模型是万能的,回归分析突出弱点有两个:
回归不等于因果!不等于因果!不等于因果!回归模型只能从数据上说明:两个变量存在关系,但是实际上有没有关系,得看具体业务情况。因此千万不要乱用。
模型检验可能难以通过。为了演示方便,本文选择的数据非常漂亮,做出来三项检测全部通过,但实际情况会很复杂,出现各种检测不通过的情况,因此也衍生出更多、更复杂的知识点,这个我们后边慢慢分享。