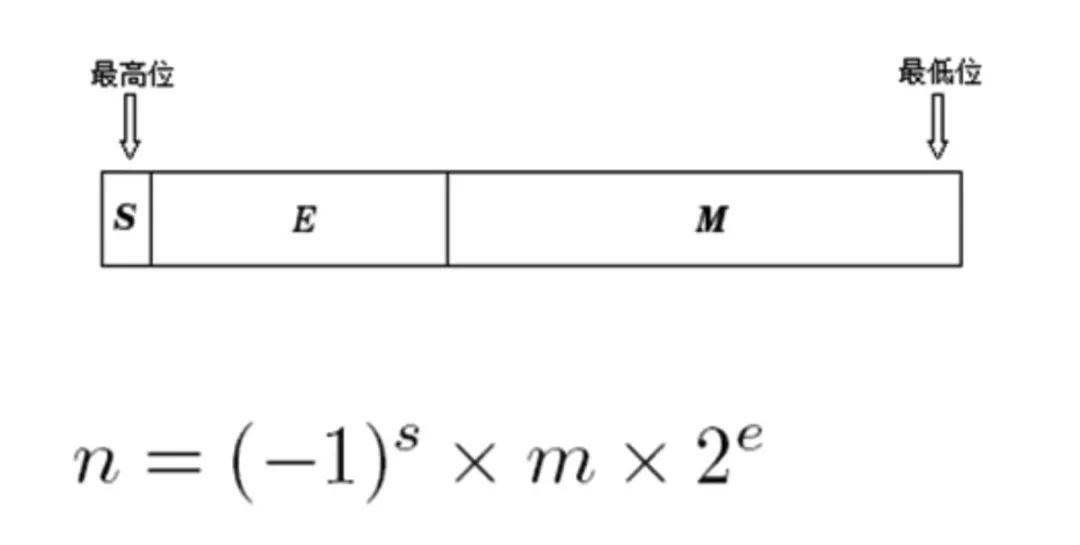浅析 Easy C++，C++ 浮点数类型-c++浮点数

浮点数是C++的第二组基本类型，它能够表示带小数部分的数字。不仅如此，浮点数的范围也比int更大，可以表示更大范围的数字。

我们都知道在计算机当中，所有数据本质上都是转化成二进制存储的。整数很简单，存储的就是转化成二进制之后的01串，那么浮点数又是如何存储的呢?

很容易猜到的是浮点数存储的结果也是二进制，但相比于整型直接转化成二进制要复杂一些。它需要先表示成下面这行式子：

这里的n即我们要存储的浮点数，s表示符号位，m是尾数，而e则是阶数。

符号位很好理解，它和整型当中的符号位一样，0表示正数，1表示负数。m表示尾数，。我们这么看很抽象，来看一个例子，比如3.0，转化成二进制是，相当于。那么，。

我们了解了浮点数的表示方式，那么它又是如何存储在计算机当中的呢?这需要我们进一步地剖析其中的细节。

首先是m，m被定义成一个大于等于1，小于2的小数。我们可以简单写成1.xx，其中xx表示的就是小数的部分。

既然它总是大于等于1，小于2的，那么它的个位一定是1，我们就可以将它省略，仅仅看之后小数的部分。小数的部分，我们同样使用二进制来逼近。比如0.625，可以表示成0.5 + 0.125，即，表示成二进制就是，只不过这里它的最高位是从-1开始的。

以32位的浮点数为例，除去1位表示符号，8位表示阶数之后，还有23位留给m。由于我们舍掉了小数点之前的1，所以我们的阶数是从-1开始的，理论上等价于24个二进制位。

在浮点数存储当中，e是一个无符号整数。以32位浮点数为例，e一共有8位，可以表示0-255。

但e是可以为负数的，根据IEEE 754的规定，e的真实值必须再减去一个中间数。对于8位的e，它的中间数是127。比如e的实际值是10，但是存储的时候需要存储成127+10=137。

除此之外，e还有另外三种情况：

关于e的规则看起来有些复杂，初看觉得有些难以理解，为什么要用减去中间值的设计，而不用符号位?后来仔细思考了一下才发现，如果引入符号位很难区分0.xxx以及e就是等于0的情况，虽然也可以特判处理，但就没有现在这样优雅了。

觉得上文看不懂的小伙伴可以直接略过这段，毕竟这个是浮点数的实现原理，算是很底层的内容了，C++ primer上对于这部分也没有过多阐述。

C++当中有两种浮点数的书写方式，第一种是使用常规的小数点表示法：

double a = 1.23; 
float b = 3.43;

另外一种写法是科学记数法，写成：

double a = 2.45e8; 
double b = 1e-7;

2.45e8表示，e之后可以跟正数也可以跟负数，但数字当中不能有空格。

和C语言一样，C++也有三种浮点数类型：float,double和long double。和整型一样，这三种类型都是浮点数，只不过表示的范围不同。

浮点数的范围有两个部分综合决定，一个部分是有效数字。比如14179是5位有效数字，而14000只有两位，因为后面三个0都是填充位，有效数字的位数不依赖小数点的位置。C++当中要求，float至少表示32位有效数字，double至少48位，而long double至少和double一样。

另外，它们能够表达的指数范围至少是-37到37。一般来说，float一共是4个字节32位，而double是8个字节64位，当然这也取决于具体的运行环境。

关于浮点数的使用有几点注意事项，千万要注意。

cout输出浮点数会删除结尾的0

书写浮点数常量时默认为double类型，如果需要强制表示为float类型，请在结尾加上后缀f或者F，如：2.34f

由于浮点数有精度，不能直接判断两个浮点数是否相等，很有可能得不到预期结果，正确的做法是判断精度范围，如：

double epsilon = 1e-8; 
// 判断a是否和b相等 
if (abs(a - b) < epsilon) { 
    // todo 
}

判断两个浮点数a和b是否相等，等价于两者的差的绝对值小于某一个精度。

范围问题，如运行下列代码将得到错误的结果：

float a = 2.3e22f; 
float b = a + 1.0f; 
 
cout << b - a << endl;

输出的结果将是0，因为2.3e22是一个小数点左边有23位的数字，加上1之后，就是在第23位加上1。但是float类型只能表示数字中的前6位或者前7位，表示不了这么高的精度，因此这个+1的操作完全没有生效。

这个问题是一个大坑，一不小心就会中招，千万要小心。

本文转载自微信公众号「Coder梁」，可以通过以下二维码关注。转载本文请联系Coder梁公众号。