本文转载自微信公众号「三分钟学前端」,作者sisterAn。转载本文请联系三分钟学前端公众号。
给定一个包含非负整数的数组,你的任务是统计其中可以组成三角形三条边的三元组个数。
示例 1:
- 输入: [2,2,3,4]
- 输出: 3
- 解释:
- 有效的组合是:
- 2,3,4 (使用第一个 2)
- 2,3,4 (使用第二个 2)
- 2,2,3
注意:
- 数组长度不超过1000。
- 数组里整数的范围为 [0, 1000]。
解法:排序+双指针
我们知道三角形的任意两边之和大于第三边,任意两边之差小于第三边,如果这三条边长从小到大为 a 、 b 、 c ,当且仅当 a + b > c 这三条边能组成三角形
解题思路: 先数组排序,排序完后,固定最长的边,利用双指针法判断其余边
以 nums[nums.length - 1] 作为最长的边 nums[k] ( k = nums.length - 1 )
以 nums[i] 作为最短边,以 nums[nums.length - 2] 作为第二个数 nums[j] ( j = nums.length - 2 ) ,
判断 nums[i] + nums[j] 是否大于 nums[k] ,
- nums[i] + nums[j] > nums[k] ,则:
- nums[i+1] + nums[j] > nums[k]
- nums[i+2] + nums[j] > nums[k]
- ...
- nums[j-1] + nums[j] > nums[k]
则可构成三角形的三元组个数加 j-i ,并且 j 往前移动一位( j-- ), 继续进入下一轮判断
- nums[i] + nums[j] <= nums[k],则 l 往后移动一位(nums 是增序排列),继续判断
代码实现:
- let triangleNumber = function(nums) {
- if(!nums || nums.length < 3) return 0
- let count = 0
- // 排序
- nums.sort((a, b) => a - b)
- for(let k = nums.length - 1; k > 1; k--){
- let i = 0, j = k - 1
- while(i < j){
- if(nums[i] + nums[j] > nums[k]){
- count += j - i
- j--
- } else {
- i++
- }
- }
- }
- return count
- }
复杂度分析:
- 时间复杂度:O(n^2^)
- 空间复杂度:O(n)
注意:
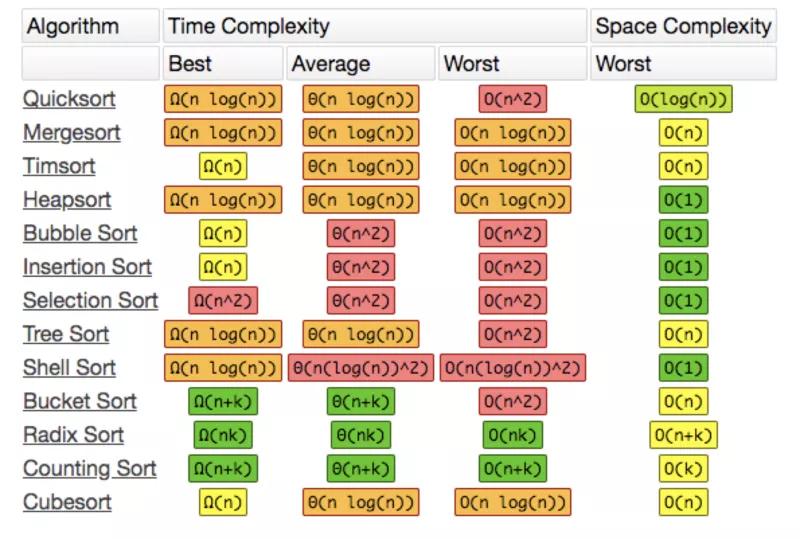
关于 Array.prototype.sort() ,ES 规范并没有指定具体的算法,在 V8 引擎中, 7.0 版本之前,数组长度小于10时, Array.prototype.sort() 使用的是插入排序,否则用快速排序。
在 V8 引擎 7.0 版本之后就舍弃了快速排序,因为它不是稳定的排序算法,在最坏情况下,时间复杂度会降级到 O(n2)。
而是采用了一种混合排序的算法:TimSort 。
这种功能算法最初用于Python语言中,严格地说它不属于以上10种排序算法中的任何一种,属于一种混合排序算法:
在数据量小的子数组中使用插入排序,然后再使用归并排序将有序的子数组进行合并排序,时间复杂度为 O(nlogn) 。
leetcode:https://leetcode-cn.com/problems/valid-triangle-number/solution/teng-xun-leetcode611you-xiao-san-jiao-xing-de-ge-s/