1959年Shell发明,第一个突破 O(n^2^) 的排序算法,是简单插入排序的改进版。它与插入排序的不同之处在于,它会优先比较距离较远的元素。
插入排序
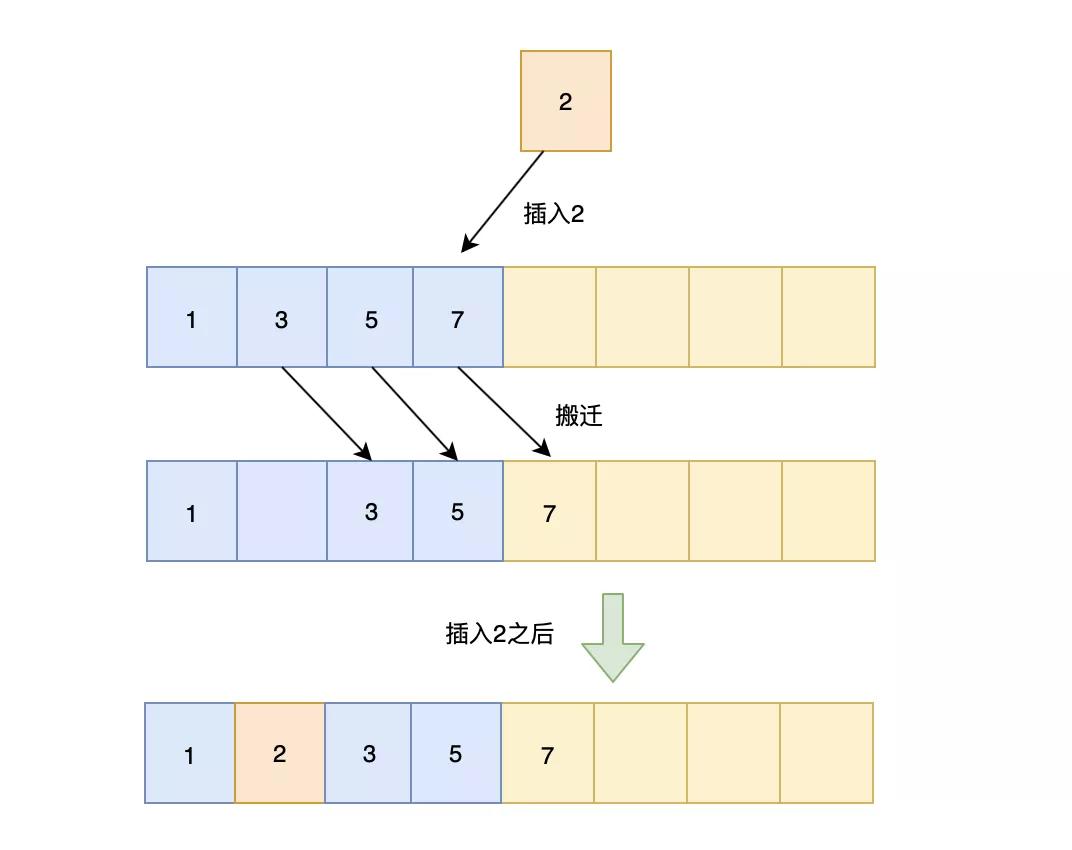
插入排序的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入
代码实现:
- function insertionSort(arr) {
- let n = arr.length;
- let preIndex, current;
- for (let i = 1; i < n; i++) {
- preIndex = i - 1;
- current = arr[i];
- while (preIndex >= 0 && arr[preIndex] > current) {
- arr[preIndex + 1] = arr[preIndex];
- preIndex--;
- }
- arr[preIndex + 1] = current;
- }
- return arr;
- }
插入算法的核心思想是取未排序区间中的元素,在已排序区间中找到合适的插入位置将其插入,并保证已排序区间数据一直有序。重复这个过程,直到未排序区间中元素为空,算法结束。
复杂度分析:
- 时间复杂度:O(n^2^)
- 空间复杂度:O(1)
希尔排序
回顾一下上面的插入排序:
- 第一趟插入排序后,我们得到的有效序列长度为 2
- 第二趟插入排序后,我们得到的有效序列长度为 3
- ...
- 直到这个序列有序
所以,如果序列足够乱的话,时间复杂度为 O(n^2^)
希尔排序又是如何优化的喃?
希尔排序又叫缩小增量排序,就是把数列进行分组(组内不停使用插入排序),直至从宏观上看起来有序,最后插入排序起来就容易了(无须多次移位或交换)。
其中组的数量称为 增量 ,显然的是,增量是不断递减的(直到增量为1)
那我们有是如何进行分组喃?
往往的: 如果一个数列有 8 个元素,我们第一趟的增量是 4 ,第二趟的增量是 2 ,第三趟的增量是 1 。如果一个数列有 18 个元素,我们第一趟的增量是 9 ,第二趟的增量是 4 ,第三趟的增量是2 ,第四趟的增量是 1
很明显我们可以用一个序列来表示增量:n/2、(n/2)/2、...、1,每次增量都/2
例如:
- let arr = [4, 1, 5, 8, 7, 3]
排序前:
将该数组看成三组( Math.floor(arr.length/2) ),分别是:[4, 1] , [5, 8] , [7, 3]
第一趟排序:
对三组数据分别进行插入排序,因此我们三个数组得到的结果为:[1, 4] , [5, 8] , [3, 7]
此时数组是这样子的:[1, 4, 5, 8, 3, 7]
第二趟排序:
- 增量减少了,上面增量是 3 ,此时增量应该为 1 了,因此把 [1, 4, 5, 8, 3, 7] 看成一个数组(从宏观上是有序的了),对其进行插入排序,直至有序
代码实现:
- function shellSort(arr) {
- let n = arr.length;
- for (let gap = Math.floor(n / 2); gap > 0; gap = Math.floor(gap / 2)) {
- for (let i = gap; i < n; i++) {
- let j = i;
- let current = arr[i];
- while (j - gap >= 0 && current < arr[j - gap]) {
- arr[j] = arr[j - gap];
- j = j - gap;
- }
- arr[j] = current;
- }
- }
- return arr;
- }
复杂度分析:
- 时间复杂度:O(nlogn)
- 空间复杂度:O(1)