全排列 II
力扣题目链接:https://leetcode-cn.com/problems/permutations-ii
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例 1:
- 输入:nums = [1,1,2]
- 输出:[[1,1,2], [1,2,1], [2,1,1]]
示例 2:
- 输入:nums = [1,2,3]
- 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
提示:
- 1 <= nums.length <= 8
- -10 <= nums[i] <= 10
思路
如果对回溯算法基础还不了解的话,我还特意录制了一期视频:带你学透回溯算法(理论篇) 可以结合题解和视频一起看,希望对大家理解回溯算法有所帮助。
这道题目和全排列的区别在与给定一个可包含重复数字的序列,要返回所有不重复的全排列。
这里又涉及到去重了。
在组合总和II 、子集II我们分别详细讲解了组合问题和子集问题如何去重。
那么排列问题其实也是一样的套路。
还要强调的是去重一定要对元素经行排序,这样我们才方便通过相邻的节点来判断是否重复使用了。
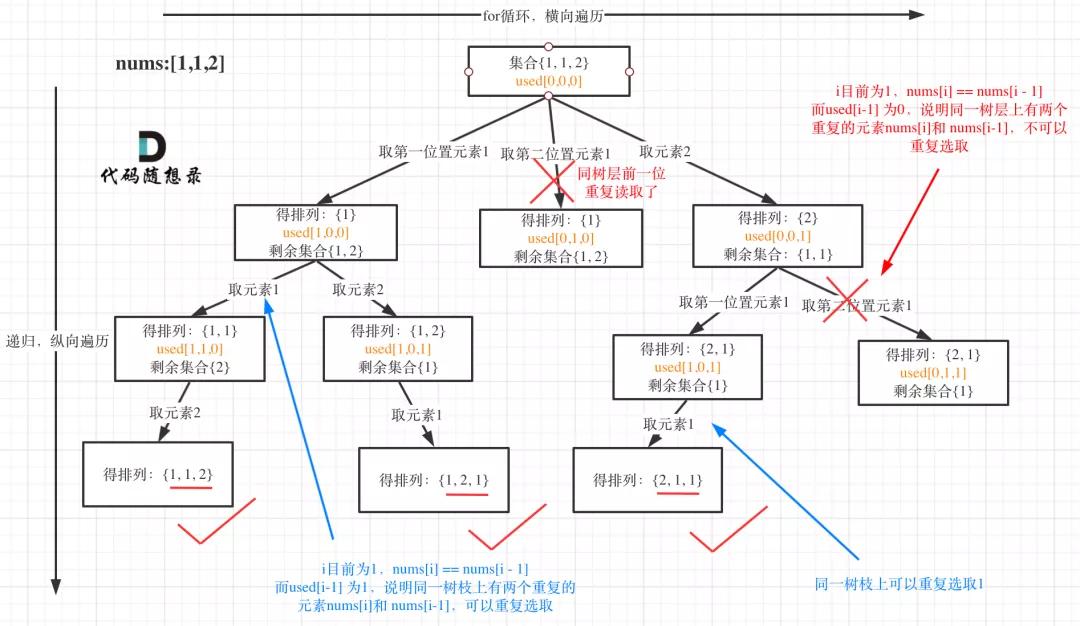
我以示例中的 [1,1,2]为例 (为了方便举例,已经排序)抽象为一棵树,去重过程如图:
全排列II1
图中我们对同一树层,前一位(也就是nums[i-1])如果使用过,那么就进行去重。
一般来说:组合问题和排列问题是在树形结构的叶子节点上收集结果,而子集问题就是取树上所有节点的结果。
在46.全排列中已经详解讲解了排列问题的写法,在40.组合总和II 、90.子集II中详细讲解的去重的写法,所以这次我就不用回溯三部曲分析了,直接给出代码,如下:
C++代码
- class Solution {
- private:
- vector<vector<int>> result;
- vector<int> path;
- void backtracking (vector<int>& nums, vector<bool>& used) {
- // 此时说明找到了一组
- if (path.size() == nums.size()) {
- result.push_back(path);
- return;
- }
- for (int i = 0; i < nums.size(); i++) {
- // used[i - 1] == true,说明同一树支nums[i - 1]使用过
- // used[i - 1] == false,说明同一树层nums[i - 1]使用过
- // 如果同一树层nums[i - 1]使用过则直接跳过
- if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
- continue;
- }
- if (used[i] == false) {
- used[i] = true;
- path.push_back(nums[i]);
- backtracking(nums, used);
- path.pop_back();
- used[i] = false;
- }
- }
- }
- public:
- vector<vector<int>> permuteUnique(vector<int>& nums) {
- result.clear();
- path.clear();
- sort(nums.begin(), nums.end()); // 排序
- vector<bool> used(nums.size(), false);
- backtracking(nums, used);
- return result;
- }
- };
拓展
大家发现,去重最为关键的代码为:
- if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
- continue;
- }
如果改成 used[i - 1] == true, 也是正确的!,去重代码如下:
- if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) {
- continue;
- }
这是为什么呢,就是上面我刚说的,如果要对树层中前一位去重,就用used[i - 1] == false,如果要对树枝前一位去重用used[i - 1] == true。
对于排列问题,树层上去重和树枝上去重,都是可以的,但是树层上去重效率更高!
这么说是不是有点抽象?
来来来,我就用输入: [1,1,1] 来举一个例子。
树层上去重(used[i - 1] == false),的树形结构如下:
全排列II2
树枝上去重(used[i - 1] == true)的树型结构如下:
全排列II
大家应该很清晰的看到,树层上对前一位去重非常彻底,效率很高,树枝上对前一位去重虽然最后可以得到答案,但是做了很多无用搜索。
总结
这道题其实还是用了我们之前讲过的去重思路,但有意思的是,去重的代码中,这么写:
- if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
- continue;
- }
和这么写:
- if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == true) {
- continue;
- }
都是可以的,这也是很多同学做这道题目困惑的地方,知道used[i - 1] == false也行而used[i - 1] == true也行,但是就想不明白为啥。
所以我通过举[1,1,1]的例子,把这两个去重的逻辑分别抽象成树形结构,大家可以一目了然:为什么两种写法都可以以及哪一种效率更高!
是不是豁然开朗了!!
本文转载自微信公众号「代码随想录」,可以通过以下二维码关注。转载本文请联系代码随想录公众号。