互联网经典算法之验证二叉搜索树-二叉树搜索算法

[[427951]]

本文转载自微信公众号「程序员小熊」，作者Dine 。转载本文请联系程序员小熊公众号。

前言

大家好，我是来自于华为的程序员小熊。今天给大家带来一道与二叉树相关的面试高频题，这道题在半年内被谷歌、字节、微软和亚马逊等大厂作为面试题，即力扣上的第98题-验证二叉搜索树。

本文主要介绍递归和深度优先搜索两种方法来解答此题，供大家参考，希望对大家有所帮助。

验证二叉搜索树

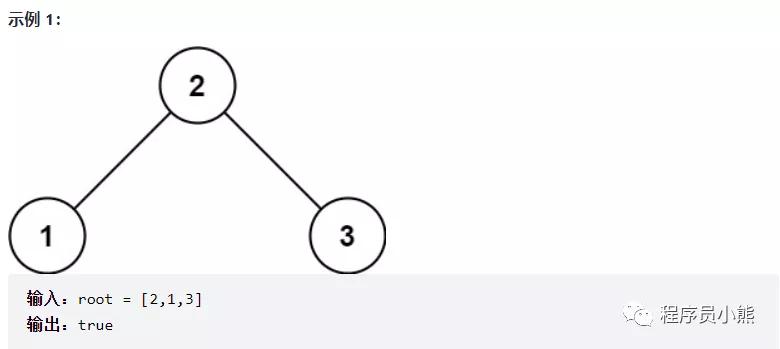
给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

节点的左子树只包含小于当前节点的数。

节点的右子树只包含大于当前节点的数。

所有左子树和右子树自身必须也是二叉搜索树。

示例 1

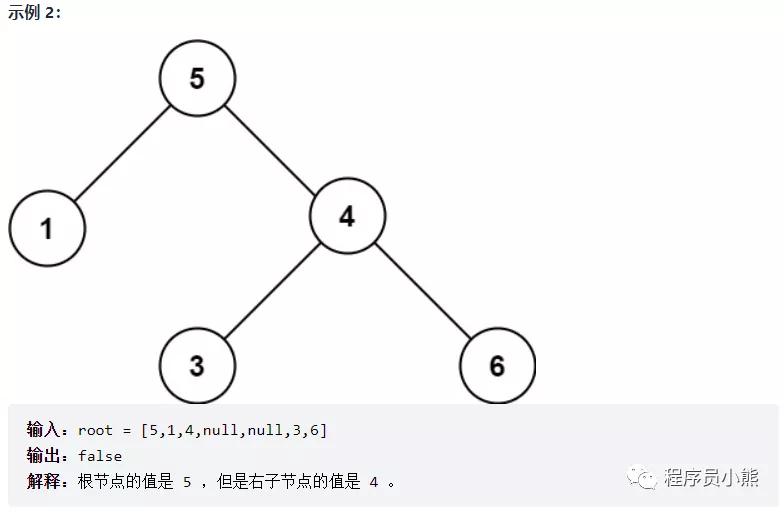
示例 2 及提示

二叉搜索树

题目已提示有效二叉搜索树的定义如下：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

举例

例 1

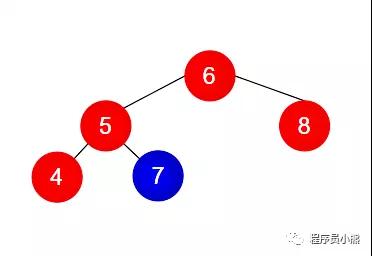
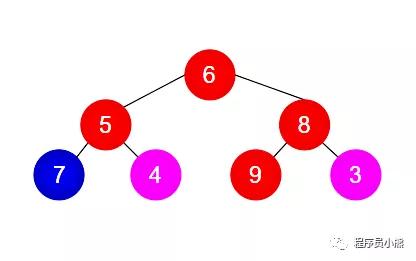
例1

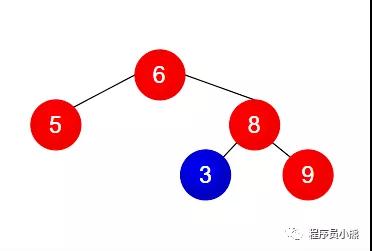
例 2

例 3

判断二叉搜索树

针对上面的举例，根据二叉搜索树的判断方法，对上面的例子是否是二叉搜索树进行如下判断：

例 1 不是二叉搜索树。原因：根节点(值为 6)的左子树中有节点(值为 7)的数大于根节点的数。
例 2 不是二叉搜索树。原因：根节点(值为 6)的右子树中有节点(值为 3)的数小于根节点的数。
例 3 不是二叉搜索树。原因：根节点的左子树不是二叉搜索树，左子树的根节点的值 5 不仅小于左子节点的值 7 还大于右子节点的值 4，并且根节点的值 6 小于左子树中节点的值 7;根节点的右子树也不是二叉搜索树，右子树的根节点的值 8 不仅大于右子节点的值 3 还小于左子节点的值 9，并且根节点的值 6 大于右子树中节点的值 3。

解题思路

根据二叉搜索树的定义，判断一棵树是否是二叉搜索树，需要判断每个节点是否符合二叉树的性质，而且判断的依据又是一样的，因此可采用递归法去解答此题。

递归

上述提到的判断的依据(假设当前节点存在左右子节点)是指：

当前节点的值大于其左子节点的值;
当前节点的值小于其右子节点的值;
如果当前节点存在左右子树，则其左右子树上的节点还要满足：左子树上的节点值小于当前节点的值，右子树上的节点值大于当前节点的值;

根据以上的思路，可以通过设置上下界，来判断节点是否符合二叉搜索树的性质。

如果存在上下界，则判断节点是否在上下界内，如不在，则不是二叉搜索树;否则以该节点的值作为上界，对其左子树进行递归判断，以该节点的值作为下界，对其右子树进行递归判断。

注意

空树属于二叉搜索树。

Show me the Code

bool isValidBST_Helper(struct TreeNode* root, double min, double max) { 
    /* 特殊判断 */ 
    if (root == NULL) { 
        return true; 
    } 
 
    /* 当前节点不在上下界内，不是二叉搜索树 */ 
    if (root->val <= min || root->val >= max) { 
        return false; 
    } 
 
    /* 判断左右子树是否是二叉搜索树 */ 
    return isValidBST_Helper(root->left, min, root->val) && isValidBST_Helper(root->right, root->val, max); 
} 
 
bool isValidBST(struct TreeNode* root) { 
    return isValidBST_Helper(root, LONG_MIN, LONG_MAX); 
}

C++

bool isValidBST_Helper(TreeNode* root, double min, double max) { 
    if (root == nullptr) { 
        return true; 
    } 
 
    if (root->val <= min || root->val >= max) { 
        return false; 
    } 
 
    return isValidBST_Helper(root->left, min, root->val) && isValidBST_Helper(root->right, root->val, max); 
} 
 
bool isValidBST(TreeNode* root) { 
    return isValidBST_Helper(root, LONG_MIN, LONG_MAX); 
}

Java

boolean isValidBST_Helper(TreeNode root, double min, double max) { 
    if (root == null) { 
        return true; 
    } 
 
    if (root.val <= min || root.val >= max) { 
        return false; 
    } 
 
    return isValidBST_Helper(root.left, min, root.val) && isValidBST_Helper(root.right, root.val, max); 
} 
 
boolean isValidBST(TreeNode root) { 
    return isValidBST_Helper(root, Long.MIN_VALUE, Long.MAX_VALUE); 
}

Python3

def isValidBST(self, root: TreeNode) -> bool: 
    def isValidBST_Helper(root, min, right): 
        if root is None: 
            return True 
         
        if root.val <= min or root.val >= right: 
            return False 
 
        return isValidBST_Helper(root.left, min, root.val) and isValidBST_Helper(root.right, root.val, right) 
 
    return isValidBST_Helper(root, -float('inf'), float('inf'))

Golang

func isValidBST(root *TreeNode) bool { 
  return isValidBST_Helper(root, math.MinInt64, math.MaxInt64) 
} 
 
func isValidBST_Helper(root *TreeNode, min, max int) bool { 
  if root == nil { 
    return true 
  } 
 
  if min >= root.Val || max <= root.Val { 
    return false 
  } 
 
  return isValidBST_Helper(root.Left, min, root.Val) && isValidBST_Helper(root.Right, root.Val, max) 
}

复杂度分析

时间复杂度：O(n)，其中 n 为二叉树节点的个数。

空间复杂度：O(n)。

深度优先搜索

根据二叉搜索树的性质，对其进行中序遍历，得到的数组一定是升序排列的。因此可以根据这个特性，判断一棵树是否是二叉搜索树。

如果采用中序遍历，将二叉树的所有节点的值存放在数组中，再去判断该数组是否是升序的，步骤有点繁琐。

由于判断数组是否是升序排列，只需要判断数组的后一个元素是否大于前一个元素即可，因此本题可以设置一个变量，用于保存中序遍历前一个节点的值，再判断当前节点的值是否大于该变量保存的值。

如果不大于，则代表该树不是二叉搜索树;否则继续遍历并判断。