ArrayList 重拳出击，把 LinkedList 干翻在地-list arraylist linkedlist

https://github.com/itwanger/toBeBetterJavaer

如果再有人给你说 “ArrayList 底层是数组，查询快、增删慢;LinkedList 底层是链表，查询慢、增删快”，你可以让他滚了!

这是一个极其不负责任的总结，关键是你会在很多地方看到这样的结论。

害，我一开始学 Java 的时候，也问过一个大佬，“ArrayList 和 LinkedList 有什么区别?”他就把“ArrayList 底层是数组，查询快、增删慢;LinkedList 底层是链表，查询慢、增删快”甩给我了，当时觉得，大佬好牛逼啊!

后来我研究了 ArrayList 和 LinkedList 的源码，发现还真的是，前者是数组，后者是 LinkedList，于是我对大佬更加佩服了!

直到后来，我亲自跑程序验证了一遍，才发现大佬的结论太草率了!根本就不是这么回事!

先来给大家普及一个概念——时间复杂度。

在计算机科学中，算法的时间复杂度(Time complexity)是一个函数，它定性描述该算法的运行时间。这是一个代表算法输入值的字符串的长度的函数。时间复杂度常用大 O 符号表述，不包括这个函数的低阶项和首项系数。使用这种方式时，时间复杂度可被称为是渐近的，亦即考察输入值大小趋近无穷时的情况。例如，如果一个算法对于任何大小为 n (必须比大)的输入，它至多需要的时间运行完毕，那么它的渐近时间复杂度是。

增删改查，对应到 ArrayList 和 LinkedList，就是 add(E e)、remove(int index)、add(int index, E element)、get(int index)，我来给大家一一分析下，它们对应的时间复杂度，也就明白了“ArrayList 底层是数组，查询快、增删慢;LinkedList 底层是链表，查询慢、增删快”这个结论很荒唐的原因

对于 ArrayList 来说：

1)get(int index) 方法的时间复杂度为，因为是直接从底层数组根据下标获取的，和数组长度无关。

public E get(int index) { 
    Objects.checkIndex(index, size); 
    return elementData(index); 
} 
1.
2.
3.
4.

这也是 ArrayList 的最大优点。

2)add(E e) 方法会默认将元素添加到数组末尾，但需要考虑到数组扩容的情况，如果不需要扩容，时间复杂度为。

public boolean add(E e) { 
    modCount++; 
    add(e, elementData, size); 
    return true; 
} 
 
private void add(E e, Object[] elementData, int s) { 
    if (s == elementData.length) 
        elementData = grow(); 
    elementData[s] = e; 
    size = s + 1; 
} 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.

如果需要扩容的话，并且不是第一次(oldCapacity > 0)扩容的时候，内部执行的 Arrays.copyOf() 方法是耗时的关键，需要把原有数组中的元素复制到扩容后的新数组当中。

private Object[] grow(int minCapacity) { 
    int oldCapacity = elementData.length; 
    if (oldCapacity > 0 || elementData != DEFAULTCAPACITY_EMPTY_ELEMENTDATA) { 
        int newCapacity = ArraysSupport.newLength(oldCapacity, 
                minCapacity - oldCapacity, /* minimum growth */ 
                oldCapacity >> 1           /* preferred growth */); 
        return elementData = Arrays.copyOf(elementData, newCapacity); 
    } else { 
        return elementData = new Object[Math.max(DEFAULT_CAPACITY, minCapacity)]; 
    } 
} 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.

3)add(int index, E element) 方法将新的元素插入到指定的位置，考虑到需要复制底层数组(根据之前的判断，扩容的话，数组可能要复制一次)，根据最坏的打算(不管需要不需要扩容，System.arraycopy() 肯定要执行)，所以时间复杂度为。

public void add(int index, E element) { 
    rangeCheckForAdd(index); 
    modCount++; 
    final int s; 
    Object[] elementData; 
    if ((s = size) == (elementData = this.elementData).length) 
        elementData = grow(); 
    System.arraycopy(elementData, index, 
            elementData, index + 1, 
            s - index); 
    elementData[index] = element; 
    size = s + 1; 
} 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.

来执行以下代码，把沉默王八插入到下标为 2 的位置上。

ArrayList<String> list = new ArrayList<>(); 
list.add("沉默王二"); 
list.add("沉默王三"); 
list.add("沉默王四"); 
list.add("沉默王五"); 
list.add("沉默王六"); 
list.add("沉默王七"); 
list.add(2, "沉默王八"); 
1.
2.
3.
4.
5.
6.
7.
8.

System.arraycopy() 执行完成后，下标为 2 的元素为沉默王四，这一点需要注意。也就是说，在数组中插入元素的时候，会把插入位置以后的元素依次往后复制，所以下标为 2 和下标为 3 的元素都为沉默王四。

之后再通过 elementData[index] = element 将下标为 2 的元素赋值为沉默王八;随后执行 size = s + 1，数组的长度变为 7。

4)remove(int index) 方法将指定位置上的元素删除，考虑到需要复制底层数组，所以时间复杂度为。

public E remove(int index) { 
    Objects.checkIndex(index, size); 
    final Object[] es = elementData; 
 
    @SuppressWarnings("unchecked") E oldValue = (E) es[index]; 
    fastRemove(es, index); 
 
    return oldValue; 
} 
private void fastRemove(Object[] es, int i) { 
    modCount++; 
    final int newSize; 
    if ((newSize = size - 1) > i) 
        System.arraycopy(es, i + 1, es, i, newSize - i); 
    es[size = newSize] = null; 
} 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.

对于 LinkedList 来说：

1)get(int index) 方法的时间复杂度为，因为需要循环遍历整个链表。

public E get(int index) { 
    checkElementIndex(index); 
    return node(index).item; 
} 
 
LinkedList.Node<E> node(int index) { 
    // assert isElementIndex(index); 
 
    if (index < (size >> 1)) { 
        LinkedList.Node<E> x = first; 
        for (int i = 0; i < index; i++) 
            x = x.next; 
        return x; 
    } else { 
        LinkedList.Node<E> x = last; 
        for (int i = size - 1; i > index; i--) 
            x = x.prev; 
        return x; 
    } 
} 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.

下标小于链表长度的一半时，从前往后遍历;否则从后往前遍历，这样从理论上说，就节省了一半的时间。

如果下标为 0 或者 list.size() - 1 的话，时间复杂度为。这种情况下，可以使用 getFirst() 和 getLast() 方法。

public E getFirst() { 
    final LinkedList.Node<E> f = first; 
    if (f == null) 
        throw new NoSuchElementException(); 
    return f.item; 
} 
 
public E getLast() { 
    final LinkedList.Node<E> l = last; 
    if (l == null) 
        throw new NoSuchElementException(); 
    return l.item; 
} 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.

first 和 last 在链表中是直接存储的，所以时间复杂度为。

2)add(E e) 方法默认将元素添加到链表末尾，所以时间复杂度为。

public boolean add(E e) { 
    linkLast(e); 
    return true; 
} 
void linkLast(E e) { 
    final LinkedList.Node<E> l = last; 
    final LinkedList.Node<E> newNode = new LinkedList.Node<>(l, e, null); 
    last = newNode; 
    if (l == null) 
        first = newNode; 
    else 
        l.next = newNode; 
    size++; 
    modCount++; 
} 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.

3)add(int index, E element) 方法将新的元素插入到指定的位置，需要先通过遍历查找这个元素，然后再进行插入，所以时间复杂度为。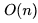

public void add(int index, E element) { 
    checkPositionIndex(index); 
 
    if (index == size) 
        linkLast(element); 
    else 
        linkBefore(element, node(index)); 
} 
1.
2.
3.
4.
5.
6.
7.
8.

如果下标为 0 或者 list.size() - 1 的话，时间复杂度为。这种情况下，可以使用 addFirst() 和 addLast() 方法。

public void addFirst(E e) { 
    linkFirst(e); 
} 
private void linkFirst(E e) { 
    final LinkedList.Node<E> f = first; 
    final LinkedList.Node<E> newNode = new LinkedList.Node<>(null, e, f); 
    first = newNode; 
    if (f == null) 
        last = newNode; 
    else 
        f.prev = newNode; 
    size++; 
    modCount++; 
} 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.

linkLast() 只需要对 last 进行更新即可。

public void addLast(E e) { 
    linkLast(e); 
} 
 
void linkLast(E e) { 
    final LinkedList.Node<E> l = last; 
    final LinkedList.Node<E> newNode = new LinkedList.Node<>(l, e, null); 
    last = newNode; 
    if (l == null) 
        first = newNode; 
    else 
        l.next = newNode; 
    size++; 
    modCount++; 
} 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.

需要注意的是，有些文章里面说，LinkedList 插入元素的时间复杂度近似，其实是有问题的，因为 add(int index, E element) 方法在插入元素的时候会调用 node(index) 查找元素，该方法之前我们之间已经确认过了，时间复杂度为，即便随后调用 linkBefore() 方法进行插入的时间复杂度为，总体上的时间复杂度仍然为才对。

void linkBefore(E e, LinkedList.Node<E> succ) { 
    // assert succ != null; 
    final LinkedList.Node<E> pred = succ.prev; 
    final LinkedList.Node<E> newNode = new LinkedList.Node<>(pred, e, succ); 
    succ.prev = newNode; 
    if (pred == null) 
        first = newNode; 
    else 
        pred.next = newNode; 
    size++; 
    modCount++; 
} 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.

4)remove(int index) 方法将指定位置上的元素删除，考虑到需要调用 node(index) 方法查找元素，所以时间复杂度为。

public E remove(int index) { 
    checkElementIndex(index); 
    return unlink(node(index)); 
} 
 
E unlink(LinkedList.Node<E> x) { 
    // assert x != null; 
    final E element = x.item; 
    final LinkedList.Node<E> next = x.next; 
    final LinkedList.Node<E> prev = x.prev; 
 
    if (prev == null) { 
        first = next; 
    } else { 
        prev.next = next; 
        x.prev = null; 
    } 
 
    if (next == null) { 
        last = prev; 
    } else { 
        next.prev = prev; 
        x.next = null; 
    } 
 
    x.item = null; 
    size--; 
    modCount++; 
    return element; 
} 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.

通过时间复杂度的比较，以及源码的分析，我相信大家在选择的时候就有了主意，对吧?

需要注意的是，如果列表很大很大，ArrayList 和 LinkedList 在内存的使用上也有所不同。LinkedList 的每个元素都有更多开销，因为要存储上一个和下一个元素的地址。ArrayList 没有这样的开销。

查询的时候，ArrayList 比 LinkedList 快，这是毋庸置疑的;插入和删除的时候，LinkedList 因为要遍历列表，所以并不比 ArrayList 更快。反而 ArrayList 更轻量级，不需要在每个元素上维护上一个和下一个元素的地址。

但是，请注意，如果 ArrayList 在增删改的时候涉及到大量的数组复制，效率就另当别论了，因为这个过程相当的耗时。

对于初学者来说，一般不会涉及到百万级别的数据操作，如果真的不知道该用 ArrayList 还是 LinkedList，就无脑选择 ArrayList 吧!

本文转载自微信公众号「沉默王二」，可以通过以下二维码关注。转载本文请联系沉默王二公众号。