给定一个整型数组, 你的任务是找到所有该数组的递增子序列,递增子序列的长度至少是2。
示例:
- 输入: [4, 6, 7, 7]
- 输出: [[4, 6], [4, 7], [4, 6, 7], [4, 6, 7, 7], [6, 7], [6, 7, 7], [7,7], [4,7,7]]
说明:
- 给定数组的长度不会超过15。
- 数组中的整数范围是 [-100,100]。
- 给定数组中可能包含重复数字,相等的数字应该被视为递增的一种情况。
思路
这个递增子序列比较像是取有序的子集。而且本题也要求不能有相同的递增子序列。
这又是子集,又是去重,是不是不由自主的想起了刚刚讲过的90.子集II。
就是因为太像了,更要注意差别所在,要不就掉坑里了!
在90.子集II中我们是通过排序,再加一个标记数组来达到去重的目的。
而本题求自增子序列,是不能对原数组经行排序的,排完序的数组都是自增子序列了。
所以不能使用之前的去重逻辑!
本题给出的示例,还是一个有序数组 [4, 6, 7, 7],这更容易误导大家按照排序的思路去做了。
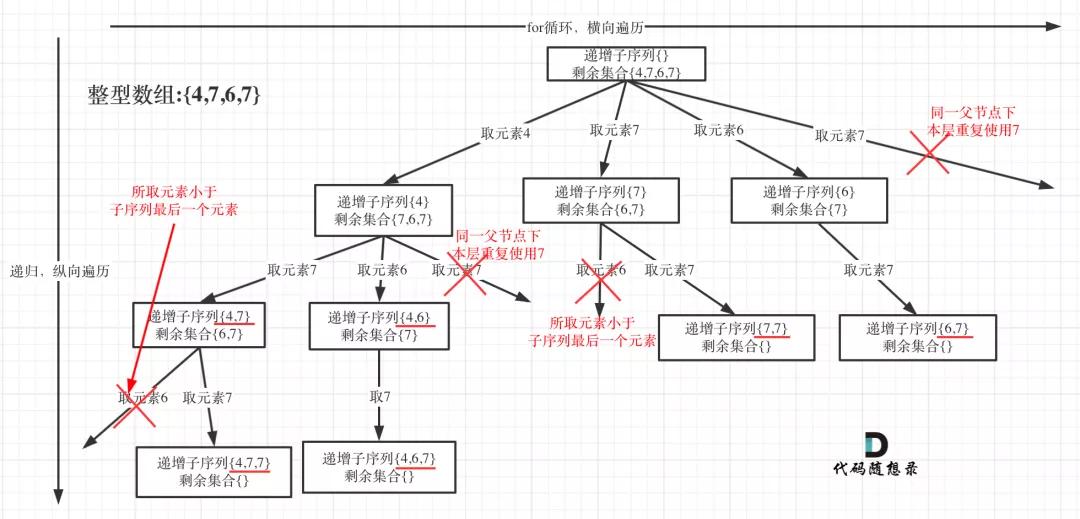
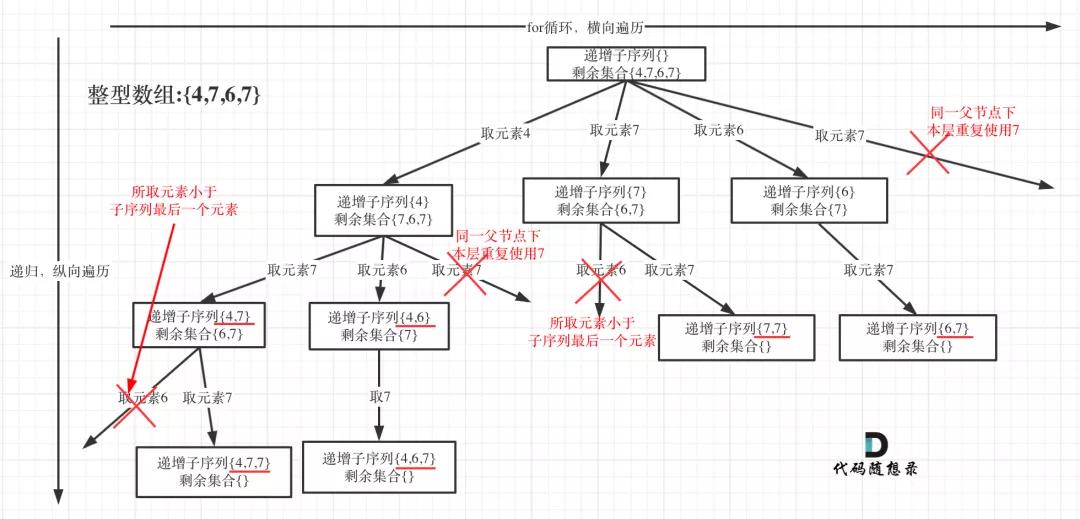
为了有鲜明的对比,我用[4, 7, 6, 7]这个数组来举例,抽象为树形结构如图:
递增子序列1
回溯三部曲
- 递归函数参数
本题求子序列,很明显一个元素不能重复使用,所以需要startIndex,调整下一层递归的起始位置。
代码如下:
- vector<vector<int>> result;
- vector<int> path;
- void backtracking(vector<int>& nums, int startIndex)
- 终止条件
本题其实类似求子集问题,也是要遍历树形结构找每一个节点,所以和回溯算法:求子集问题!一样,可以不加终止条件,startIndex每次都会加1,并不会无限递归。
但本题收集结果有所不同,题目要求递增子序列大小至少为2,所以代码如下:
- if (path.size() > 1) {
- result.push_back(path);
- // 注意这里不要加return,因为要取树上的所有节点
- }
- 单层搜索逻辑
在图中可以看出,同一父节点下的同层上使用过的元素就不能在使用了
那么单层搜索代码如下:
- unordered_set<int> uset; // 使用set来对本层元素进行去重
- for (int i = startIndex; i < nums.size(); i++) {
- if ((!path.empty() && nums[i] < path.back())
- || uset.find(nums[i]) != uset.end()) {
- continue;
- }
- uset.insert(nums[i]); // 记录这个元素在本层用过了,本层后面不能再用了
- path.push_back(nums[i]);
- backtracking(nums, i + 1);
- path.pop_back();
- }
对于已经习惯写回溯的同学,看到递归函数上面的uset.insert(nums[i]);,下面却没有对应的pop之类的操作,应该很不习惯吧,哈哈
这也是需要注意的点,unordered_set
最后整体C++代码如下:
- // 版本一
- class Solution {
- private:
- vector<vector<int>> result;
- vector<int> path;
- void backtracking(vector<int>& nums, int startIndex) {
- if (path.size() > 1) {
- result.push_back(path);
- // 注意这里不要加return,要取树上的节点
- }
- unordered_set<int> uset; // 使用set对本层元素进行去重
- for (int i = startIndex; i < nums.size(); i++) {
- if ((!path.empty() && nums[i] < path.back())
- || uset.find(nums[i]) != uset.end()) {
- continue;
- }
- uset.insert(nums[i]); // 记录这个元素在本层用过了,本层后面不能再用了
- path.push_back(nums[i]);
- backtracking(nums, i + 1);
- path.pop_back();
- }
- }
- public:
- vector<vector<int>> findSubsequences(vector<int>& nums) {
- result.clear();
- path.clear();
- backtracking(nums, 0);
- return result;
- }
- };
优化
以上代码用我用了unordered_set
其实用数组来做哈希,效率就高了很多。
注意题目中说了,数值范围[-100,100],所以完全可以用数组来做哈希。
程序运行的时候对unordered_set 频繁的insert,unordered_set需要做哈希映射(也就是把key通过hash function映射为唯一的哈希值)相对费时间,而且每次重新定义set,insert的时候其底层的符号表也要做相应的扩充,也是费事的。
那么优化后的代码如下:
- // 版本二
- class Solution {
- private:
- vector<vector<int>> result;
- vector<int> path;
- void backtracking(vector<int>& nums, int startIndex) {
- if (path.size() > 1) {
- result.push_back(path);
- }
- int used[201] = {0}; // 这里使用数组来进行去重操作,题目说数值范围[-100, 100]
- for (int i = startIndex; i < nums.size(); i++) {
- if ((!path.empty() && nums[i] < path.back())
- || used[nums[i] + 100] == 1) {
- continue;
- }
- used[nums[i] + 100] = 1; // 记录这个元素在本层用过了,本层后面不能再用了
- path.push_back(nums[i]);
- backtracking(nums, i + 1);
- path.pop_back();
- }
- }
- public:
- vector<vector<int>> findSubsequences(vector<int>& nums) {
- result.clear();
- path.clear();
- backtracking(nums, 0);
- return result;
- }
- };
这份代码在leetcode上提交,要比版本一耗时要好的多。
所以正如在哈希表:总结篇!(每逢总结必经典)中说的那样,数组,set,map都可以做哈希表,而且数组干的活,map和set都能干,但如果数值范围小的话能用数组尽量用数组。
总结
本题题解清一色都说是深度优先搜索,但我更倾向于说它用回溯法,而且本题我也是完全使用回溯法的逻辑来分析的。
相信大家在本题中处处都能看到是90.子集II的身影,但处处又都是陷阱。
对于养成思维定式或者套模板套嗨了的同学,这道题起到了很好的警醒作用。更重要的是拓展了大家的思路!
就酱,如果感觉「代码随想录」很干货,就帮Carl宣传一波吧!
本文转载自微信公众号「代码随想录」,可以通过以下二维码关注。转载本文请联系代码随想录公众号。