本文转载自微信公众号「高性能架构探索」,作者雨乐。转载本文请联系高性能架构探索公众号。
今年,北京的雨尤其多,淅淅沥沥的。整个中秋节前两天,都是在雨中度过,没了往日中秋节的快乐气氛,幸运的是,在中秋节当天,天气晴朗,算是对整个假期画上了个还算满意的句号。
听着淅淅沥沥的雨声,想起前段时间在脉脉上看了一篇帖子,阿里P8去面试某条,挂在了一面算法上。而自己在3年前面试某公司,也栽在了同样的一道算法上。正所谓吃一堑长一智,把该算法题重新整理了下,分享给大家,希望能够有用。
接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
接雨水
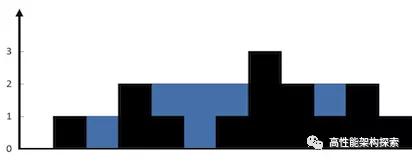
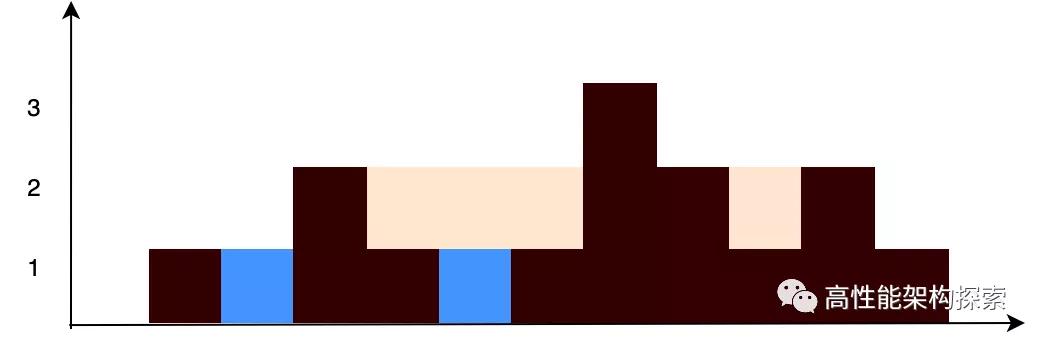
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6
解释:上面是由数组[0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接6个单位的雨水(蓝色部分表示雨水)
看到题目的第一眼,感觉很简单,但是却不知道从何入手。下面我们将遵循循序渐进的方式,分析此题目的解法。
暴力解法
看到题目的一刻,出于思维定式,必定去查找"凹"型槽的最低部分,然后。。。,如此如此,越来越头大,直至放弃。
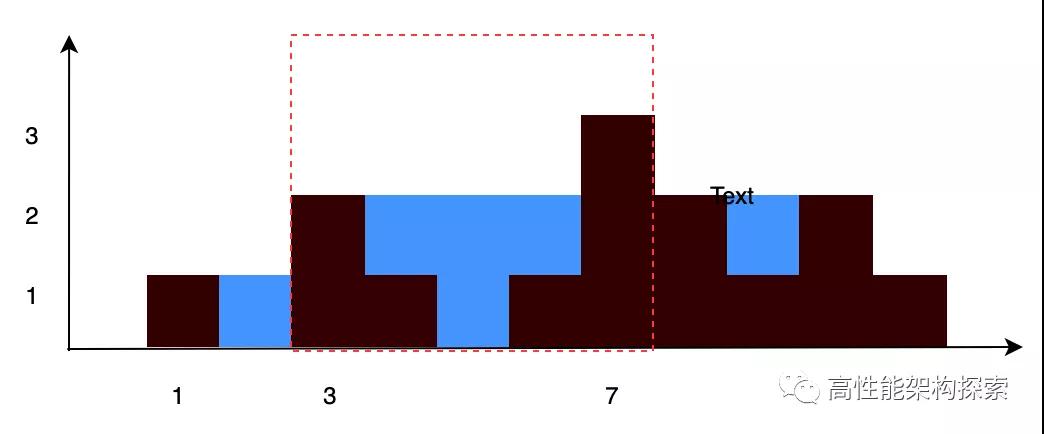
我们不妨换个思路,每根柱子上能放多少雨水。那么每根柱子上盛放雨水的高度怎么计算呢?就是其左右两边柱子最大高度的较小者与其高度之差,文字上理解起来比较费力,用图的方式更加便于大家理解。
下面我们将计算柱子坐标(3)-(7)即红框内的盛水量。
我们首先定义4个变量:
- res 盛水总量,其初始化为0
- height 当前柱子高度
- left_max 左边最大高度(包括当前柱子本身
- right_max 右边最大高度(包括其本身)
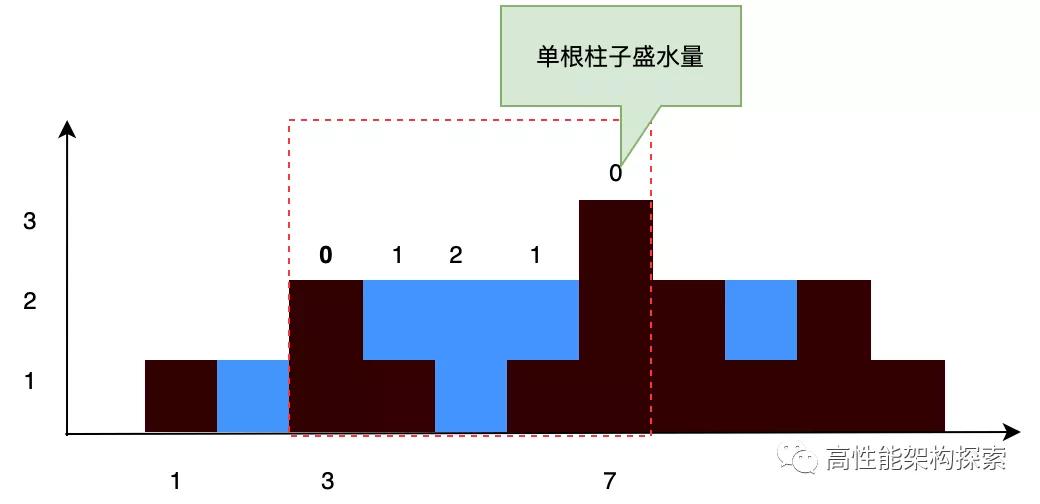
首先,计算柱子(3)处其盛水量。其左边最大高度left_max为2,右边最大高度right_max为3,那么横坐标3处盛水量为min(left_max, right_max) - height 赋值之后为min(2, 3) - 2,答案为0,也就是说柱子(3)可盛水量为0。
接着我们计算柱子(4)处盛水量。按照上述计算规则,左边最大高度为2,右边最大高度为3,那么柱子(4)可盛水量为min(2, 3)- 1,答案为1。
然后计算柱子(5)处的盛水量,按照上述计算规则,左边最大高度为2,右边最大高度为3,那么柱子(5)可盛水量为min(2, 3)- 0,答案为2。
然后计算柱子(6)处的盛水量,按照上述计算规则,左边最大高度为2,右边最大高度为3,那么柱子(6)可盛水量为min(2, 3)- 1,答案为1。
最后计算柱子(7)处的盛水量,左边最大高度为3,右边最大高度为3,那么柱子(7)可盛水量为min(3, 3) - 3即0.
因此,柱子(3)到柱子(7)之间所盛水量res = 0 + 1 + 2 + 1 + 0 = 4.
代码实现一:
- int trap(vector<int>& height) {
- int res = 0;
- for (int cur = 0; cur < height.size(); ++cur) {
- int left_max = 0;
- int right_max = 0;
- // 计算左边最大高度
- for (int left = 0; left <= cur; ++left) {
- left_max = std::max(left_max, height[left]);
- }
- // 计算右边最大高度
- for (int right = cur; right < height.size(); ++right) {
- right_max = std::max(right_max, height[right]);
- }
- // 计算总盛水量
- res += std::min(left_max, right_max) - height[cur];
- }
- return res;
- }
上述规则有个trick,就是计算两边最高的时候,都将柱子本身的高度计算在内,这样做是为了在计算盛水量的时候,方便计算。
假设计算柱子(3),如果在计算两边最大高度的时候不包括柱子(3)本身的高度,那么柱子(3)左边最大高度为1,右边最大高度为3,在计算盛水量的时候,就需要判min(lext_max, right_max)与柱子(3)本身的大小,否则会出现负值,代码实现如下。
代码实现二
- int trap(vector<int>& height) {
- int res = 0;
- for (int cur = 0; cur < height.size(); ++cur) {
- int left_max = 0;
- int right_max = 0;
- // 计算左边最大高度
- // 注意,与实现一相比,left到cur的前一个截止
- for (int left = 0; left < cur; ++left) {
- left_max = std::max(left_max, height[left]);
- }
- // 计算右边最大高度
- // 注意,与实现一相比,right从下一个开始
- for (int right = cur + 1; right < height.size(); ++right) {
- right_max = std::max(right_max, height[right]);
- }
- // 计算总盛水量
- int mx = std::min(left_max, right_max);
- if (mx > height[cur]) { // 需要进行判断
- res += mx - height[cur];
- }
- }
- return res;
- }
暴力解法,理解起来简单,时间复杂度为O(n2),提交之后,毫无疑问会TLE,下面我们从其他方面对暴力法进行优化。
为了便于理解,后面的实现将使用实现二的思想。
动态规划
看了暴力法的实现,我们基本思路已经有了,其时间复杂度为O(n2),时间主要消耗在查找两边最大柱子高度上。那么有没有什么办法,能够 常数次 遍历就能获取到所有柱子的两边高度呢?
我们仍然以
- height = [0,1,0,2,1,0,1,3,2,1,2,1]
为例,计算双边最大值。
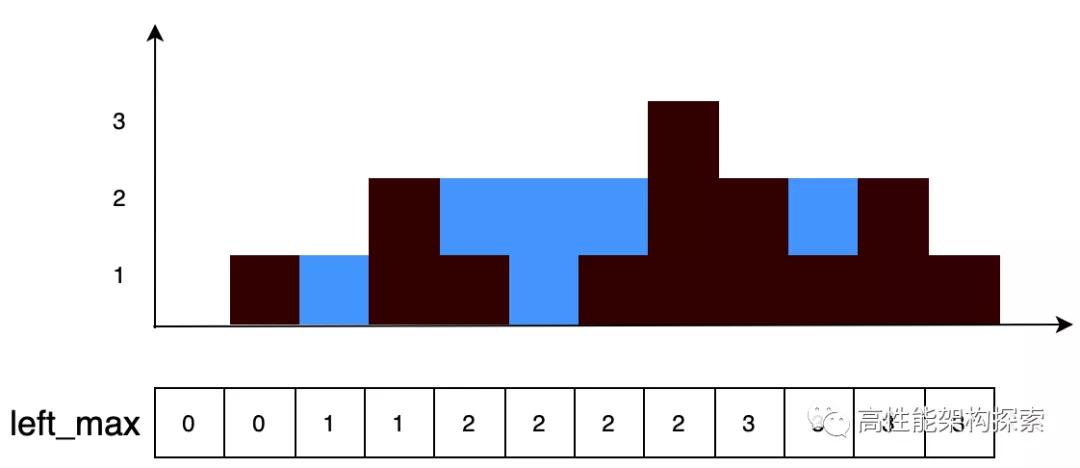
左侧最大值
定义数组left_max,其中left_max[i]代码第i个柱子左边最大高度。
下面我们来计算柱子左侧的最大高度:
- 柱子(0),左侧最大高度为0(其左侧没有柱子)
- 柱子(1),左侧最大高度为0(左侧只有柱子0)
- 柱子(2),左侧最大高度为1([0 1]数组的最大值)
- 柱子(3),左侧最大高度为1([0 1 0]数组最大值)
- 柱子(4),左侧最大高度为2([0 1 0 2]数组最大值)
- 柱子(5),左侧最大高度为2([0 1 0 2 1]数组最大值)
- 柱子(6),左侧最大高度为2([0 1 0 2 1 0]数组最大值)
- 柱子(7),左侧最大高度为2([0 1 0 2 1 0 1]数组最大值)
- 柱子(8),左侧最大高度为3([0 1 0 2 1 0 1 3]数组最大值)
- 柱子(9),左侧最大高度为3([0 1 0 2 1 0 1 3 2]数组最大值)
- 柱子(10),左侧最大高度为3([0 1 0 2 1 0 1 3 2 1]数组最大值)
- 柱子(11),左侧最大高度为3([0 1 0 2 1 0 1 3 2 1 2]数组最大值)
左侧最大值
从上述规则,我们进行分析,发现有一定的规律可循,即当前柱子左侧最大高度 为 max(上一个柱子左侧最大高度, 上一个柱子高度)。
代码表示如下:
- std::vector<int> left_max(height.size(), 0);
- for (int i = 1; i < height.size(); ++i) {
- left_max[i] = std::max(left_max[i - 1], height[i]);
- }
对上述代码进行稍许变化后如下:
- std::vector<int> left_max(height.size(), 0);
- int mx = 0;
- for (int i = 0; i < height.size(); ++i) {
- left_max[i] = mx;
- mx = std::max(mx, height[i]);
- }
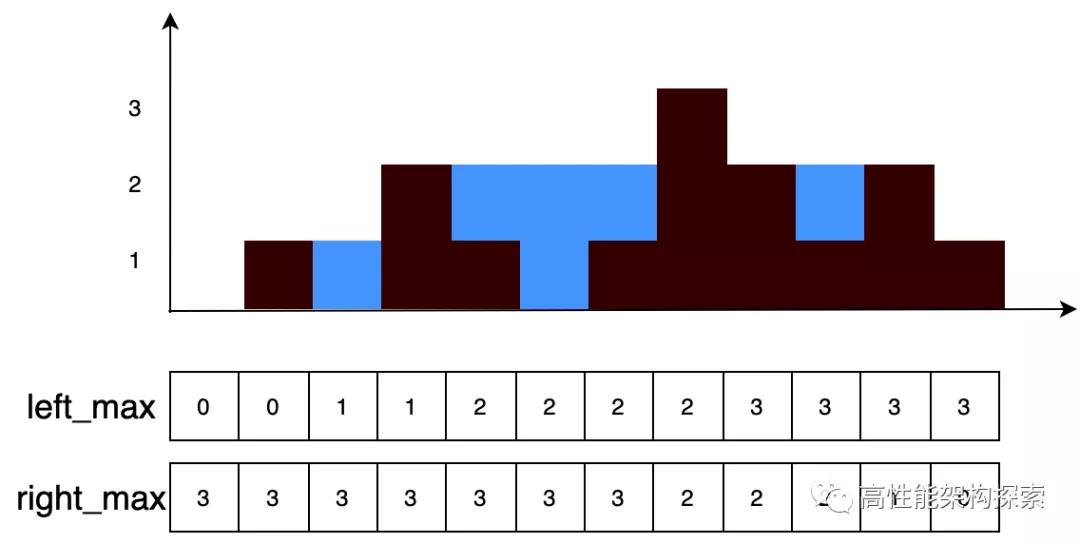
右侧最大值
定义数组right_max,其中left_max[i]代码第i个柱子右边最大高度。
因为要计算右侧最大值,所以必须从最后一个开始向前计算(如果从第一个开始计算的,那么跟暴力法没区别了)。height = [0,1,0,2,1,0,1,3,2,1,2,1]
- 柱子(11),右侧最大高度为0(其右侧没有柱子)
- 柱子(10),右侧最大高度为1([1]的最大值)
- 柱子(9),右侧最大高度为2([2 1]的最大值)
- 柱子(8),右侧最大高度为2([1 2 1]的最大值)
- 柱子(7),右侧最大高度为2([2 1 2 1]的最大值)
- 柱子(6),右侧最大高度为3([3 2 1 2 1]的最大值)
- 柱子(5),右侧最大高度为3([1 3 2 1 2 1]的最大值)
- 柱子(4),右侧最大高度为3([0 1 3 2 1 2 1]的最大值)
- 柱子(3),右侧最大高度为3([1 0 1 3 2 1 2 1]的最大值)
- 柱子(2),右侧最大高度为3([2 1 0 1 3 2 1 2 1]的最大值)
- 柱子(1),右侧最大高度为3([0 2 1 0 1 3 2 1 2 1]的最大值)
- 柱子(0),右侧最大高度为3([1 0 2 1 0 1 3 2 1 2 1]的最大值)
右侧最大值
既然计算出来了双边最大值,那么我们来实现下代码:
- int trap(vector<int>& height) {
- int res = 0;
- std::vector<int> left_max(height.size());
- std::vector<int> right_max(height.size());
- int mx = 0;
- // 循环一、计算左侧最大值
- for (int i = 0; i < height.size(); ++i) {
- left_max[i] = mx;
- mx = std::max(mx, height[i]);
- }
- mx = 0;
- // 循环二、计算右侧最大值
- for (int i = height.size() - 1; i >= 0; --i) {
- right_max[i] = mx;
- mx = std::max(mx, height[i]);
- }
- // 循环三、计算所盛雨水量
- for (int i = 0; i < height.size(); ++i) {
- int mn = std::min(left_max[i], right_max[i]);
- if (mn > height[i]) {
- res += mn - height[i];
- }
- }
- return res;
- }
上述代码较暴力方法优化后,时间复杂度优化为O(n), 提交后AE。
动态规划
上述代码中有3个循环,空间复杂度为O(2n),又作为c++ coder这是不能忍的,能不能再进行优化呢?我们看到循环三单纯为计算盛雨量,能否将循环二和循环3合并,并且优化空间复杂度呢?必须可以,为了阅读起来方便,我们实现代码如下:
- int trap(vector<int>& height) {
- int res = 0;
- std::vector<int> v(height.size());
- int mx = 0;
- // 循环一、计算左侧最大值
- for (int i = 0; i < height.size(); ++i) {
- v[i] = mx;
- mx = std::max(mx, height[i]);
- }
- mx = 0;
- // 循环二、计算右侧最大值 并 计算盛水量
- for (int i = height.size() - 1; i >= 0; --i) {
- int mn = std::min(mx, v[i]);
- mx = std::max(mx, height[i]);
- if (mn > height[i]) {
- res += mn - height[i];
- }
- }
- return res;
- }
优化后的动态规划
双指针
动态规划方法,时间复杂度和空间复杂度都是O(n),下面我们介绍一种只有一次循环且空间复杂度为O(1)的算法,这就是双指针算法。
接雨水算法的核心思想,就是计算当前柱子的盛水量,也就是左右两边的最大值的较小者与当前柱子之差。我们先求出数组双端柱子的较小值,然后两边柱子跟这个较小值相比较,如果较小值为左边的柱子,则左边柱子向右移动,直至比当前较小值大。反之,如果较小值为右侧柱子,则右侧柱子向左移动,直至比当前值大。
left 和 right 两个指针分别指向数组的首尾位置,从两边向中间扫描,在当前两指针确定的范围内,先比较两头找出较小值,如果较小值是 left 指向的值,则从左向右扫描,如果较小值是 right 指向的值,则从右向左扫描,若遇到的值比当较小值小,则将差值存入结果,如遇到的值大,则重新确定新的窗口范围,以此类推直至 left 和 right 指针重合
- int trap(vector<int>& height) {
- int res = 0;
- int left = 0;
- int right = height.size() - 1;
- while (left < right) {
- int mn = min(height[left], height[right]);
- if (mn == height[left]) {
- ++left;
- while (left < right && height[left] < mn) {
- res += mn - height[left++];
- }
- } else {
- --right;
- while (left < right && height[right] < mn) {
- res += mn - height[right--];
- }
- }
- }
- return res;
- }
单调栈
此种方法较前面的两种(暴力法和双指针法),如果说前面两种方法都是求每根柱子上盛水量之和的话(即 按列计算),那么单调栈方法则是 按行计算 每一层的盛水量,如下图所示:
逐层计算
每一行水左右肯定都会被柱子卡住。那么从左向右遍历柱子,如果高度在下降,那么显然不会蓄水。如果高度上升了,那就说明中间是个低点,这之间可以蓄水。而这个下降的高度用单调栈来维护就行了,栈里我们只放下标。
遍历高度,如果此时栈为空,或者当前高度小于等于栈顶高度,则把当前高度的坐标压入栈,注意这里不直接把高度压入栈,而是把坐标压入栈,这样方便在后来算水平距离。当遇到比栈顶高度大的时候,就说明有可能会有坑存在,可以装雨水。此时栈里至少有一个高度,如果只有一个的话,那么不能形成坑,直接跳过,如果多余一个的话,那么此时把栈顶元素取出来当作坑,新的栈顶元素就是左边界,当前高度是右边界,只要取二者较小的,减去坑的高度,长度就是右边界坐标减去左边界坐标再减1,二者相乘就是盛水量。
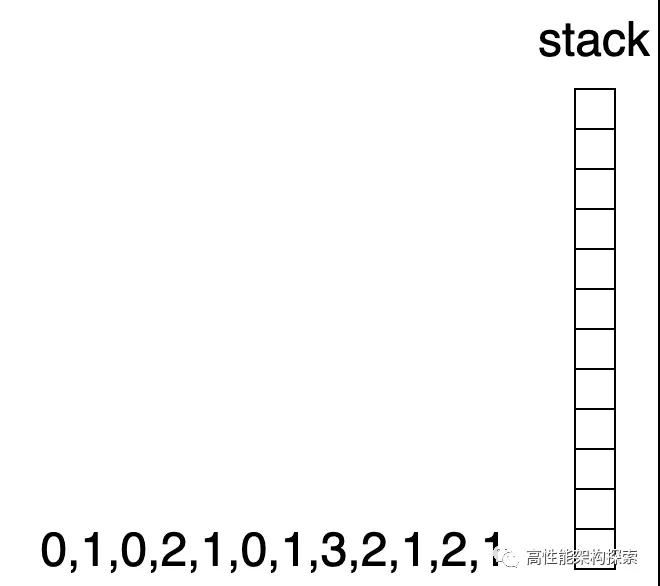
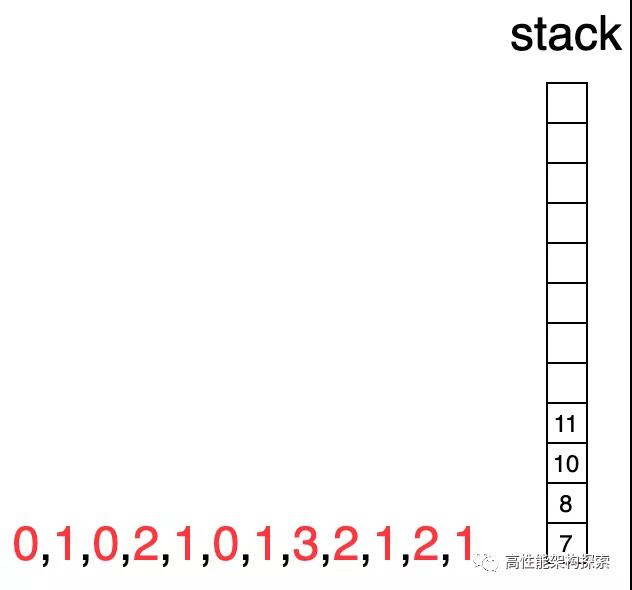
我们仍然以数组height = [0,1,0,2,1,0,1,3,2,1,2,1]为例来说明单调栈的用法。
假设res初始值为0,用其来计算height数组所表示的柱子高度最大盛水量。
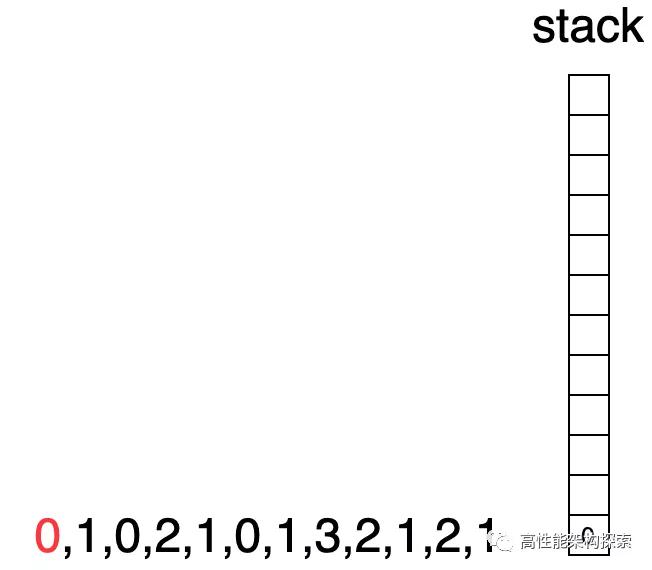
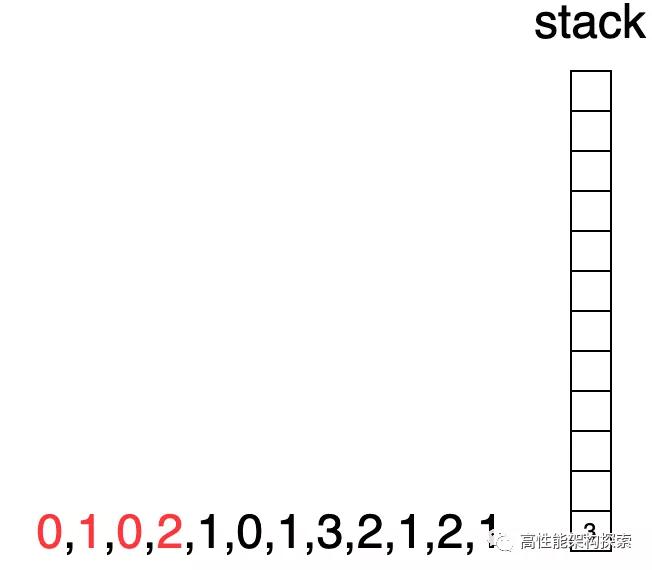
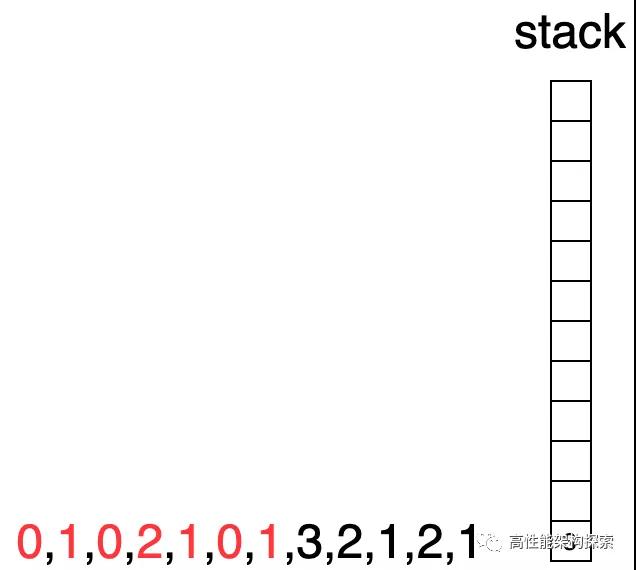
- 初始化时候,栈为空。
栈为空
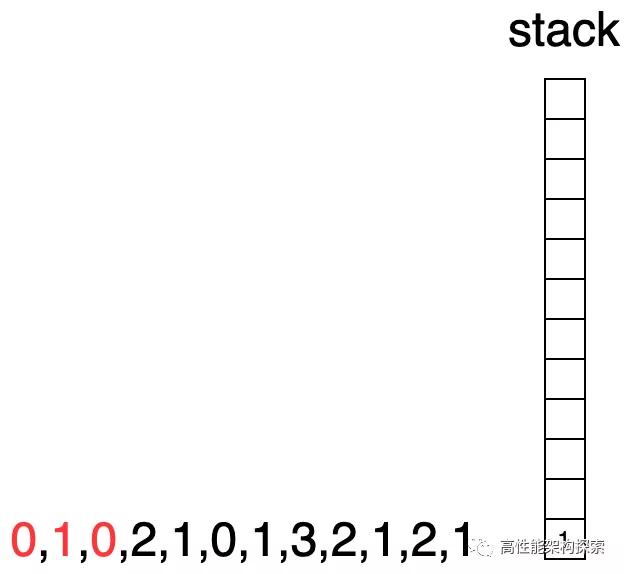
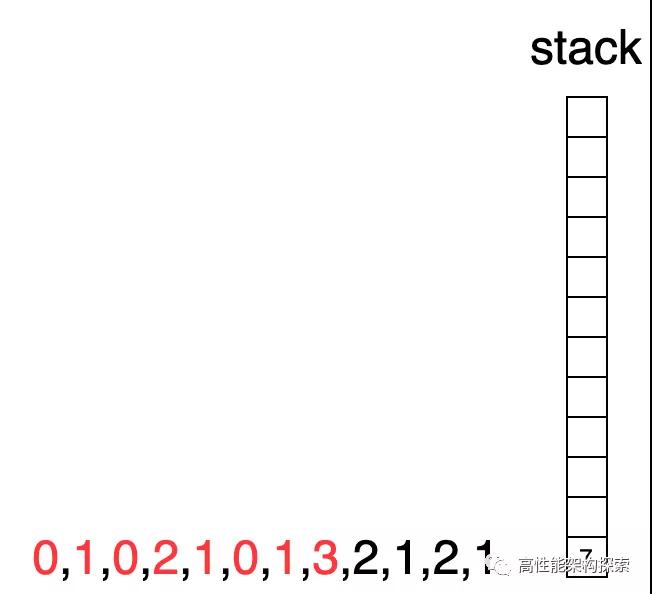
此时下标指向3,由于下标3指向的值大于栈顶下标指向的值,则出栈,计算增量盛水量((min(2, 1) - 0) * (3 - 1 - 1) = 1),即增量为1,此时res = 1。
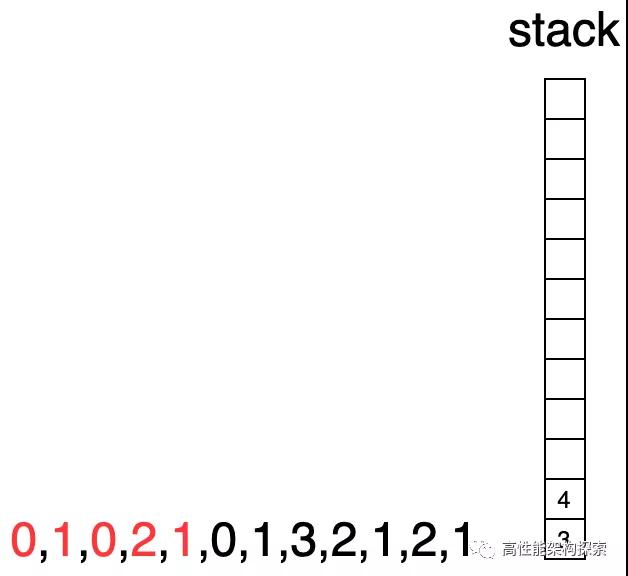
- 由于下标1所指向的高度小于下标3指向高度,则下标1出栈,此时栈为空,则下标3进栈。
- 下标4指向的值小于栈顶下标指向的值(1 < 2),下标4入栈
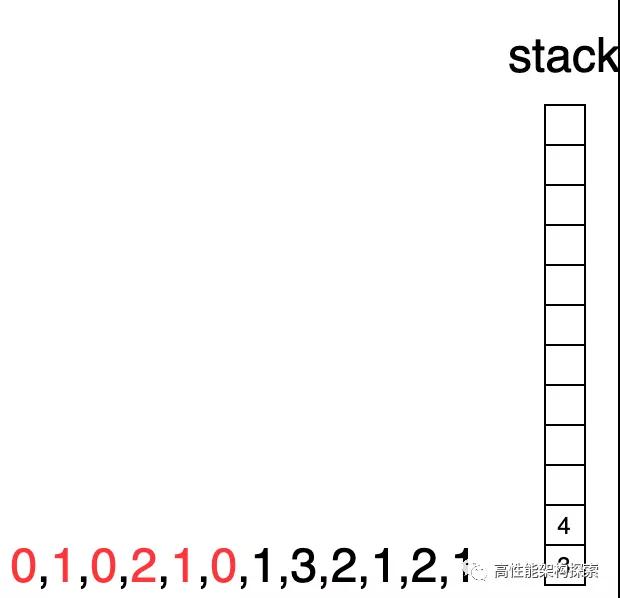
- 下标5指向的值小于栈顶下标指向的值(0 < 1),下标5入栈
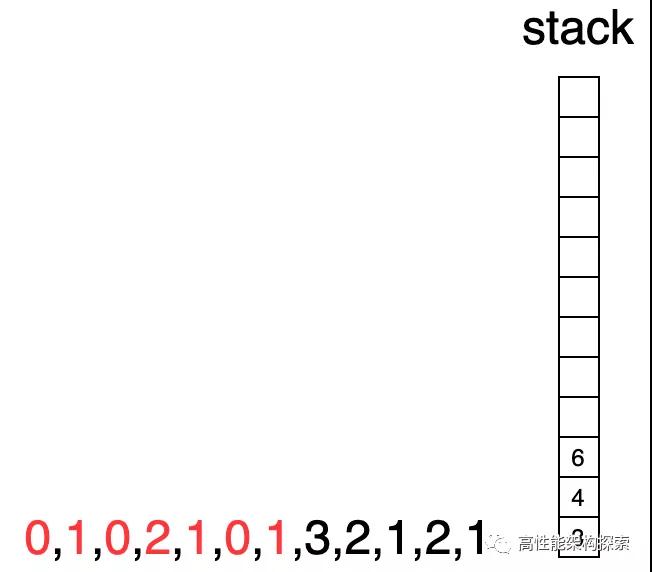
- 此时下标6指向的值为1,大于栈顶下标所指向的值(1 > 0),则执行出栈,同时计算盛水增量((min(1, 1) - 0) * (6 - 4 - 1)),增量为1,此时res = 1 + 1 = 2。
- 下标6所指向的值等于栈顶指向的值(1 = 1),下标6入栈
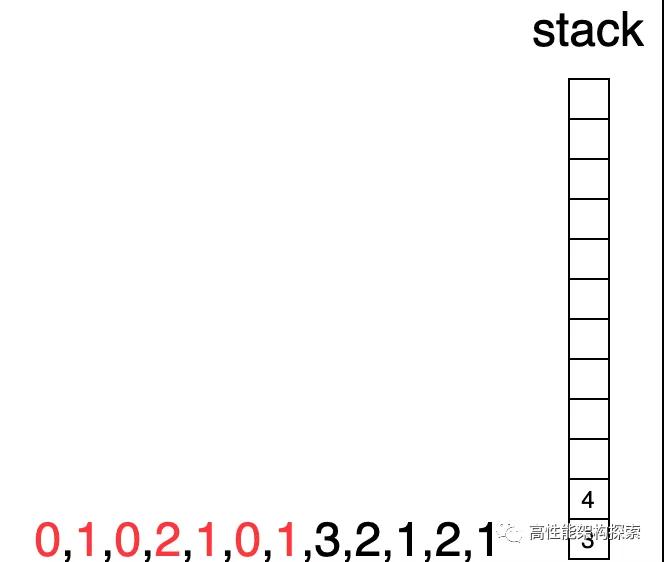
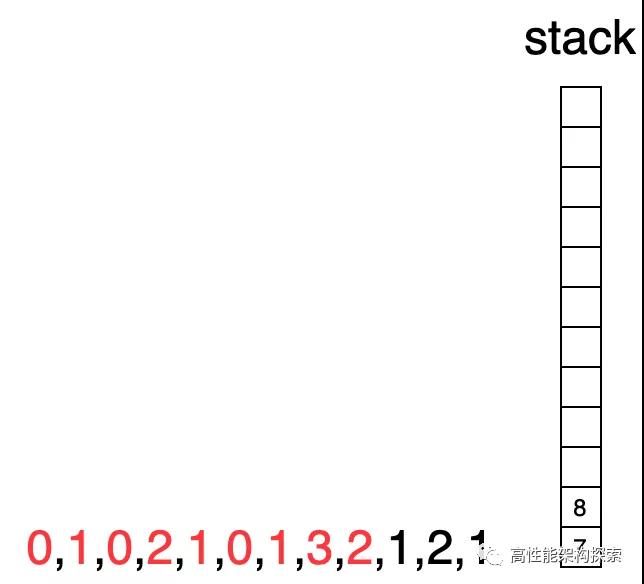
- 此时下标指向7,其值大于栈顶值(3 > 1),则栈顶出栈,计算增量为((min(3, 1) - 1) * (7 - 4 - 1)),增量为0,此时res = 1 + 1 + 0 = 2
- 此时,下标仍为7,栈顶值为4,由于当前下标指向值大于栈顶指向值,则出栈,计算盛水增量((min(3, 2) - 1) * (7 - 3 - 1)),增量为3,此时res = 1 + 1 + 0 + 3 = 5
计算增量盛水量
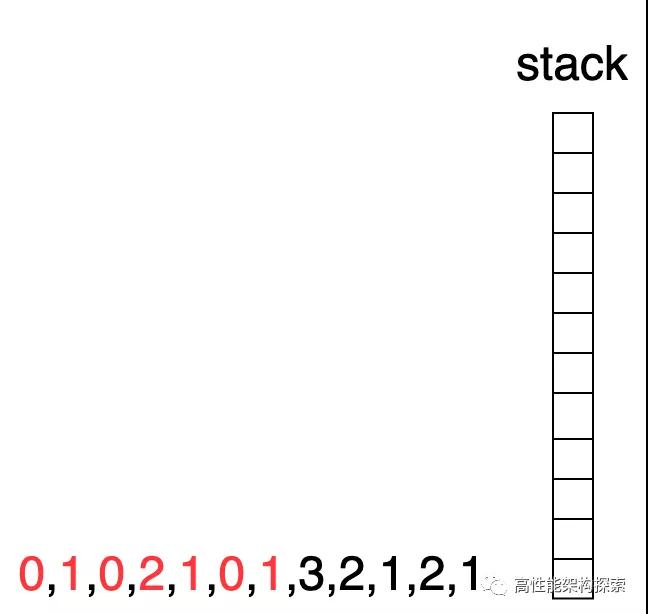
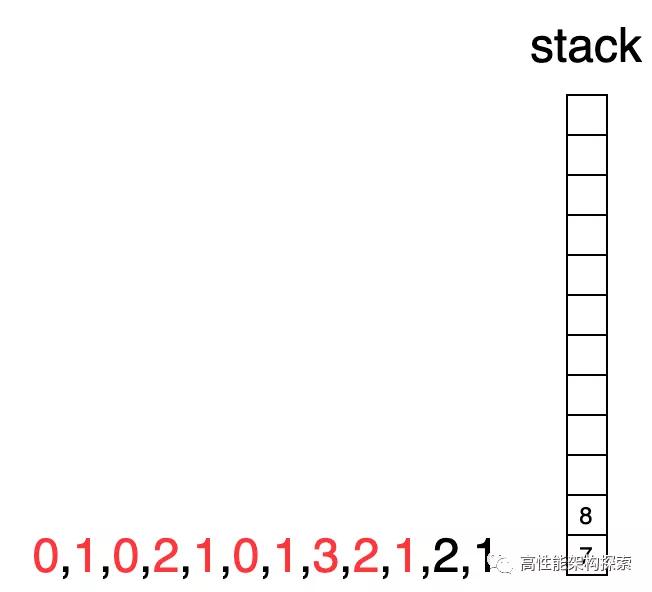
- 此时栈内只有下标3,且其所指向值小于当前下标指向值(2 < 3),则出栈
下标3出栈
此时栈为空,则下标7入栈
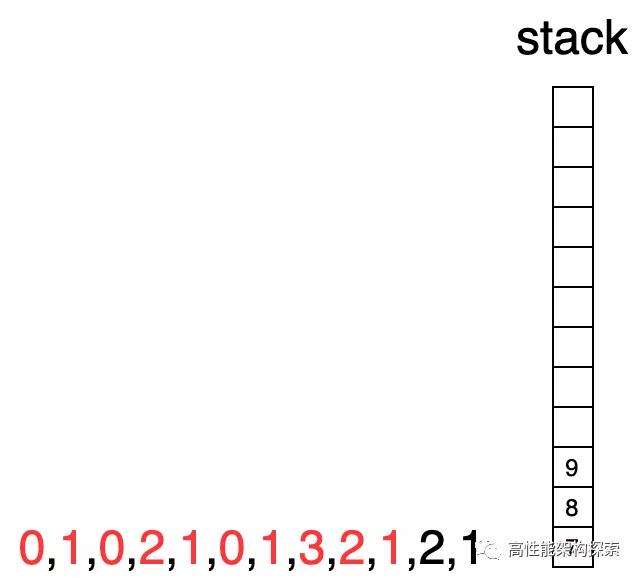
- 下标8指向值小于栈顶指向值(2 < 3),下标8入栈
- 下标9指向值小于栈顶指向值(1 < 2),下标9入栈
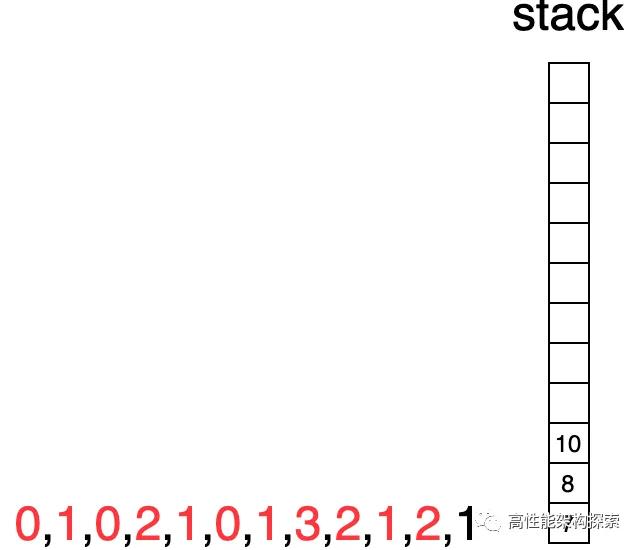
- 此时下标为10,其对应值大于栈顶指向值(2 > 1),则栈顶出栈,并计算增量((min(2, 2) - 1) * (10 - 8 - 1)),增量为1,此时res = 1 + 1 + 0 + 3 + 1 = 6
- 下标10指向值小于栈顶值,入栈
下标11指向值小于栈顶值,入栈
此时,数组循环结束,尽管栈内还有数,坐标为7 8 10 11,指向的值为3 2 2 1,但其已经不能构成一个凹槽进行盛水,所以算法执行结束。
代码实现如下:
- int trap(vector<int>& height) {
- stack<int> st;
- int i = 0, res = 0, n = height.size();
- while (i < n) {
- if (st.empty() || height[i] <= height[st.top()]) {
- st.push(i++);
- } else {
- int t = st.top(); st.pop();
- if (st.empty()) continue;
- res += (min(height[i], height[st.top()]) - height[t]) * (i - st.top() - 1);
- }
- }
- return res;
- }
写在最后
架构或者底层原理分析方面,需要调研大量的资料,研究分析源码,很耗费精力。所以后面的文章中,可能会有算法(leetcode经典算法)、面试(针对面试中遇到的一些经典问题)以及架构和底层穿插发表。