用 Python 分析资产收益的典型化事实

[[426550]]

      Python中文社区（ID:python-china）

典型化事实（Stylized Facts）是在实际数据中发现的一些现象。“典型化事实”在经济学中非常重要，无论是宏观经济学还是贸易、金融还是产业经济学，在理论的发展中都扮演着非常重要的角色，因而如果能发现一些“典型化事实”，对经济学的理论研究和之后的实证研究是非常重要的。扫描本文最下方二维码获取全部完整源码和Jupyter Notebook 文件打包下载。

典型化事实（Stylized Facts）是出现在许多资产回报（跨时间和市场）中的统计属性。了解它们很重要，因为当我们构建代表资产价格动态的模型时，模型必须能够捕获这些属性。

下面我们使用从 1985 年到 2018 年标普 500 指数的每日回报收益来分析五个典型化事实。

我们从雅虎财经下载标准普尔 500 指数价格并计算收益。使用以下代码导入所有需要的库： 

import pandas as pd   
import numpy as np  
import yfinance as yf  
import seaborn as sns   
import scipy.stats as scs  
import statsmodels.api as sm  
import statsmodels.tsa.api as smt 

在本节中，我们将用 Python去发现标准普尔 500 指数系列中的五个典型化事实。 

df = yf.download('^GSPC',   
                 start='1985-01-01', 
                 end='2018-12-31',  
                 progress=False)  
dfdf = df[['Adj Close']].rename(columns={'Adj Close': 'adj_close'})  
df['log_rtn'] = np.log(df.adj_close/df.adj_close.shift(1))  
dfdf = df[['adj_close', 'log_rtn']].dropna(how = 'any') 

一、资产收益的非高斯分布

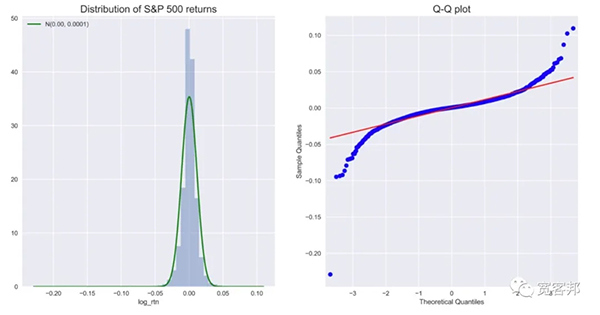
运行以下步骤，通过绘制收益直方图和 Q-Q 图来发现第一个事实的存在。

1、使用观察到的收益的均值和标准差计算正态概率密度函数 (PDF)： 

r_range = np.linspace(min(df.log_rtn), max(df.log_rtn), num=1000)  
mu = df.log_rtn.mean()  
sigma = df.log_rtn.std()  
norm_pdf = scs.norm.pdf(r_range, loc=mu, scale=sigma) 

2、绘制直方图和 Q-Q 图： 

fig, ax = plt.subplots(1, 2, figsize=(16, 8))  
# histogram  
sns.distplot(df.log_rtn, kde=False, norm_hist=True, axax=ax[0])                                  
ax[0].set_title('Distribution of S&P 500 returns', fontsize=16)                                                     
ax[0].plot(r_range, norm_pdf, 'g', lw=2,  
           label=f'N({mu:.2f}, {sigma**2:.4f})')  
ax[0].legend(loc='upper left');  
# Q-Q plot  
qq = sm.qqplot(df.log_rtn.values, line='s', axax=ax[1])  
ax[1].set_title('Q-Q plot', fontsize = 16)  
# plt.tight_layout() 
# plt.savefig('images/ch1_im10.png')  
plt.show() 

执行上面的代码会产生下图：

我们可以使用直方图（显示分布的形状）和 Q-Q 图来评估收益的正态性。此外，我们可以打印汇总统计信息：

通过查看均值、标准差、偏度和峰度等指标，我们可以推断它们偏离我们在正态下的预期。此外，Jarque-Bera 正态性检验让我们有理由拒绝原假设，即在 99% 置信水平下分布是正态的。

二、波动集聚性

运行以下代码，通过绘制收益序列来发现第二个典型化事实。

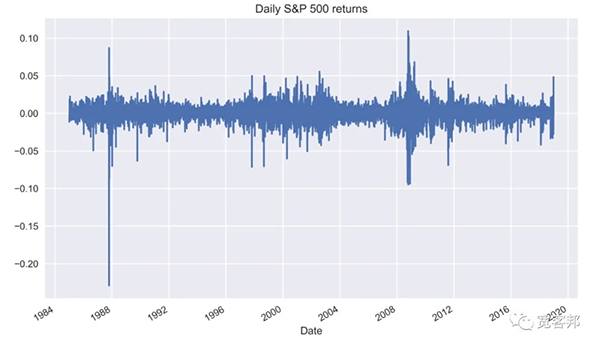
1、可视化收益序列： 

df.log_rtn.plot(title='Daily S&P 500 returns', figsize=(10, 6)) 

执行代码会产生下图：

我们可以观察到明显的波动集聚性——波动较大的正收益和负收益时期。

三、收益不存在自相关性

我们继续去发现第三个典型化事实。

1、定义用于创建自相关图的参数： 

N_LAGS = 50  
SIGNIFICANCE_LEVEL = 0.05 

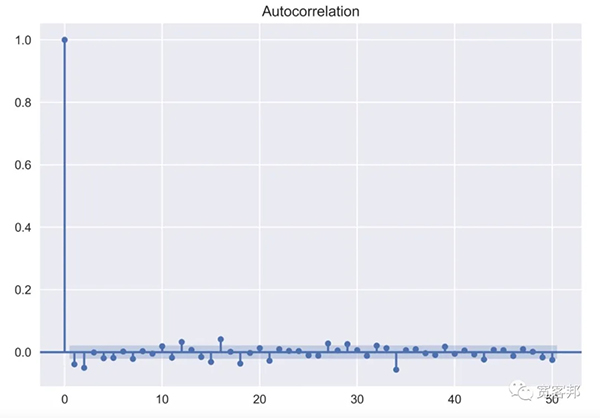
2、运行以下代码以创建收益的自相关函数 (ACF) 图： 

acf = smt.graphics.plot_acf(df.log_rtn,   
                            lags=N_LAGS,   
                            alpha=SIGNIFICANCE_LEVEL) 

执行上面的代码会产生下图：

只有少数值位于置信区间之外并且可以被认为具有统计显著性。我们可以假设已经验证了收益序列中没有自相关性。

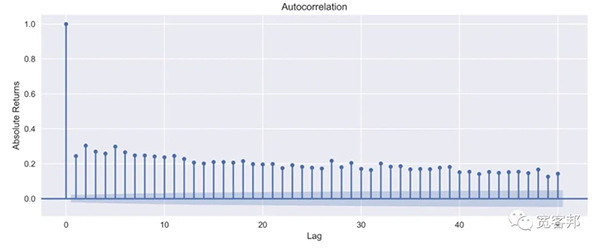
四、平方/绝对收益的自相关性小且递减

通过创建平方和绝对收益的 ACF 图来研究第四个典型化事实。

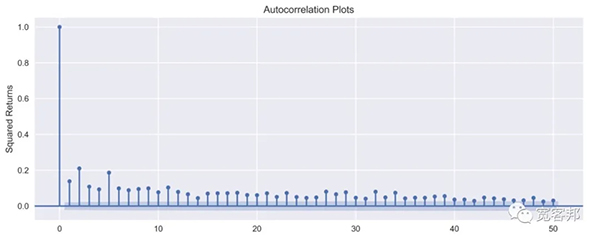
1、创建 ACF 图： 

fig, ax = plt.subplots(2, 1, figsize=(12, 10))  
smt.graphics.plot_acf(df.log_rtn ** 2, lags=N_LAGS,   
                      alpha=SIGNIFICANCE_LEVEL, axax = ax[0])  
ax[0].set(title='Autocorrelation Plots',  
          ylabel='Squared Returns')  
smt.graphics.plot_acf(np.abs(df.log_rtn), lags=N_LAGS,  
                      alpha=SIGNIFICANCE_LEVEL, axax = ax[1])  
ax[1].set(ylabel='Absolute Returns',  
          xlabel='Lag') 

执行上面的代码会产生以下图：

我们可以观察到平方回报和绝对回报的自相关值很小且不断减小，这与第四种典型化事实一致。

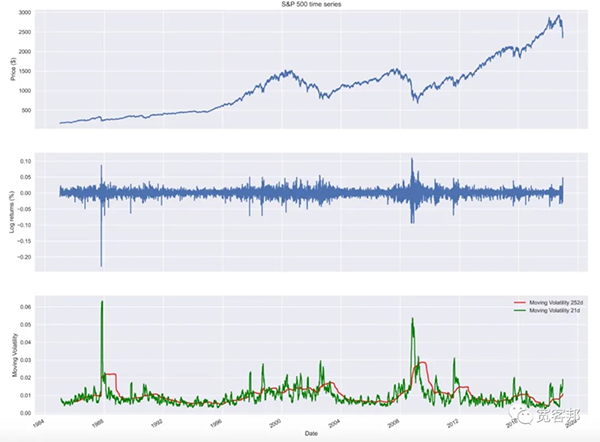
五、杠杆效应

对于第五个事实，运行以下步骤来调查杠杆效应的存在。

1、将波动性度量计算为滚动标准偏差： 

df['moving_std_252'] = df[['log_rtn']].rolling(window=252).std()  
df['moving_std_21'] = df[['log_rtn']].rolling(window=21).std() 

2、绘制所有系列以进行比较： 

fig, ax = plt.subplots(3, 1, figsize=(18, 15),   
                       sharex=True)  
df.adj_close.plot(axax=ax[0])  
ax[0].set(title='S&P 500 time series',  
          ylabel='Price ($)')  
df.log_rtn.plot(axax=ax[1])  
ax[1].set(ylabel='Log returns (%)')  
df.moving_std_252.plot(axax=ax[2], color='r', 
                       label='Moving Volatility 252d')  
df.moving_std_21.plot(axax=ax[2], color='g',   
                      label='Moving Volatility 21d')  
ax[2].set(ylabel='Moving Volatility',  
          xlabel='Date')  
ax[2].legend() 

我们现在可以通过将价格序列与（滚动）波动率指标进行可视化比较来研究杠杆效应：

这一事实表明，资产波动性的大多数衡量标准与其回报呈负相关，我们确实可以观察到价格下跌时波动性增加而价格上涨时波动性减少的模式。