复原IP地址
给定一个只包含数字的字符串,复原它并返回所有可能的 IP 地址格式。
有效的 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 '.' 分隔。
例如:"0.1.2.201" 和 "192.168.1.1" 是 有效的 IP 地址,但是 "0.011.255.245"、"192.168.1.312" 和 "192.168@1.1" 是 无效的 IP 地址。
示例 1:
- 输入:s = "25525511135"
- 输出:["255.255.11.135","255.255.111.35"]
示例 2:
- 输入:s = "0000"
- 输出:["0.0.0.0"]
示例 3:
- 输入:s = "1111"
- 输出:["1.1.1.1"]
示例 4:
- 输入:s = "010010"
- 输出:["0.10.0.10","0.100.1.0"]
示例 5:
- 输入:s = "101023"
- 输出:["1.0.10.23","1.0.102.3","10.1.0.23","10.10.2.3","101.0.2.3"]
提示:
- 0 <= s.length <= 3000
- s 仅由数字组成
思路
做这道题目之前,最好先把131.分割回文串这个做了。
这道题目相信大家刚看的时候,应该会一脸茫然。
其实只要意识到这是切割问题,切割问题就可以使用回溯搜索法把所有可能性搜出来,和刚做过的131.分割回文串就十分类似了。
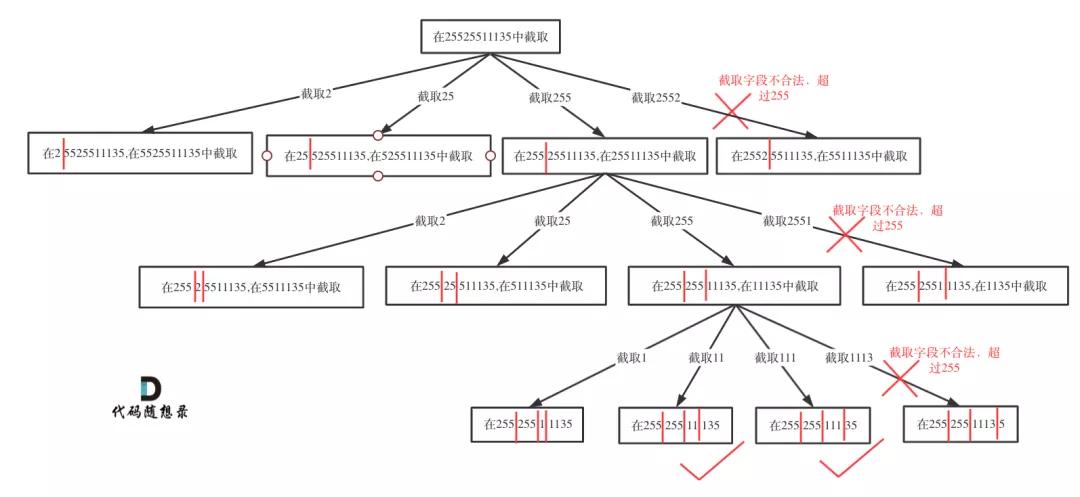
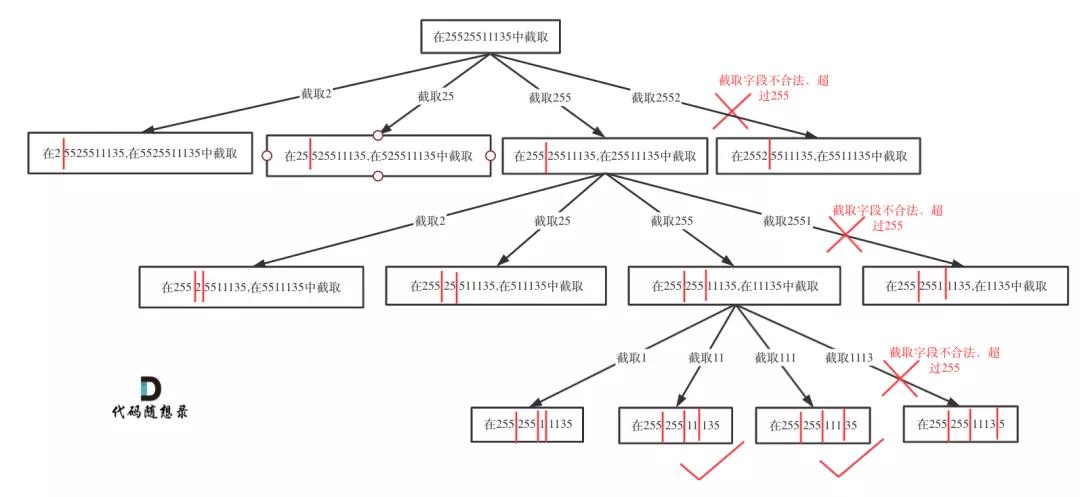
切割问题可以抽象为树型结构,如图:
复原IP地址
回溯三部曲
- 递归参数
在131.分割回文串中我们就提到切割问题类似组合问题。
startIndex一定是需要的,因为不能重复分割,记录下一层递归分割的起始位置。
本题我们还需要一个变量pointNum,记录添加逗点的数量。
所以代码如下:
vector<string> result;// 记录结果
// startIndex: 搜索的起始位置,pointNum:添加逗点的数量
void backtracking(string& s, int startIndex, int pointNum) {
- 1.
- 2.
- 3.
- 递归终止条件
终止条件和131.分割回文串情况就不同了,本题明确要求只会分成4段,所以不能用切割线切到最后作为终止条件,而是分割的段数作为终止条件。
pointNum表示逗点数量,pointNum为3说明字符串分成了4段了。
然后验证一下第四段是否合法,如果合法就加入到结果集里
代码如下:
if (pointNum == 3) { // 逗点数量为3时,分隔结束
// 判断第四段子字符串是否合法,如果合法就放进result中
if (isValid(s, startIndex, s.size() - 1)) {
result.push_back(s);
}
return;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 单层搜索的逻辑
在131.分割回文串中已经讲过在循环遍历中如何截取子串。
在for (int i = startIndex; i < s.size(); i++)循环中 [startIndex, i]这个区间就是截取的子串,需要判断这个子串是否合法。
如果合法就在字符串后面加上符号.表示已经分割。
如果不合法就结束本层循环,如图中剪掉的分支:
复原IP地址
然后就是递归和回溯的过程:
递归调用时,下一层递归的startIndex要从i+2开始(因为需要在字符串中加入了分隔符.),同时记录分割符的数量pointNum 要 +1。
回溯的时候,就将刚刚加入的分隔符. 删掉就可以了,pointNum也要-1。
代码如下:
for (int i = startIndex; i < s.size(); i++) {
if (isValid(s, startIndex, i)) { // 判断 [startIndex,i] 这个区间的子串是否合法
s.insert(s.begin() + i + 1 , '.'); // 在i的后面插入一个逗点
pointNum++;
backtracking(s, i + 2, pointNum); // 插入逗点之后下一个子串的起始位置为i+2
pointNum--; // 回溯
s.erase(s.begin() + i + 1); // 回溯删掉逗点
} else break; // 不合法,直接结束本层循环
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
判断子串是否合法
最后就是在写一个判断段位是否是有效段位了。
主要考虑到如下三点:
- 段位以0为开头的数字不合法
- 段位里有非正整数字符不合法
- 段位如果大于255了不合法
代码如下:
// 判断字符串s在左闭又闭区间[start, end]所组成的数字是否合法
bool isValid(const string& s, int start, int end) {
if (start > end) {
return false;
}
if (s[start] == '0' && start != end) { // 0开头的数字不合法
return false;
}
int num = 0;
for (int i = start; i <= end; i++) {
if (s[i] > '9' || s[i] < '0') { // 遇到非数字字符不合法
return false;
}
num = num * 10 + (s[i] - '0');
if (num > 255) { // 如果大于255了不合法
return false;
}
}
return true;
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
C++代码
根据关于回溯算法,你该了解这些!给出的回溯算法模板:
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
可以写出如下回溯算法C++代码:
class Solution {
private:
vector<string> result;// 记录结果
// startIndex: 搜索的起始位置,pointNum:添加逗点的数量
void backtracking(string& s, int startIndex, int pointNum) {
if (pointNum == 3) { // 逗点数量为3时,分隔结束
// 判断第四段子字符串是否合法,如果合法就放进result中
if (isValid(s, startIndex, s.size() - 1)) {
result.push_back(s);
}
return;
}
for (int i = startIndex; i < s.size(); i++) {
if (isValid(s, startIndex, i)) { // 判断 [startIndex,i] 这个区间的子串是否合法
s.insert(s.begin() + i + 1 , '.'); // 在i的后面插入一个逗点
pointNum++;
backtracking(s, i + 2, pointNum); // 插入逗点之后下一个子串的起始位置为i+2
pointNum--; // 回溯
s.erase(s.begin() + i + 1); // 回溯删掉逗点
} else break; // 不合法,直接结束本层循环
}
}
// 判断字符串s在左闭又闭区间[start, end]所组成的数字是否合法
bool isValid(const string& s, int start, int end) {
if (start > end) {
return false;
}
if (s[start] == '0' && start != end) { // 0开头的数字不合法
return false;
}
int num = 0;
for (int i = start; i <= end; i++) {
if (s[i] > '9' || s[i] < '0') { // 遇到非数字字符不合法
return false;
}
num = num * 10 + (s[i] - '0');
if (num > 255) { // 如果大于255了不合法
return false;
}
}
return true;
}
public:
vector<string> restoreIpAddresses(string s) {
result.clear();
if (s.size() > 12) return result; // 算是剪枝了
backtracking(s, 0, 0);
return result;
}
};
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
- 45.
- 46.
- 47.
- 48.
- 49.
- 50.
总结
在131.分割回文串中我列举的分割字符串的难点,本题都覆盖了。
而且本题还需要操作字符串添加逗号作为分隔符,并验证区间的合法性。
可以说是131.分割回文串的加强版。
在本文的树形结构图中,我已经把详细的分析思路都画了出来,相信大家看了之后一定会思路清晰不少!
本文转载自微信公众号「代码随想录」,可以通过以下二维码关注。转载本文请联系代码随想录公众号。