前面介绍的堆结构只能对数据进行部分排序,也就是它只能知道部分元素的排序,例如从根节点出发,沿着左孩子或右孩子前行,我们能得知所遍历的元素一定是递增(小堆)或是递减(大堆)关系,但是我们无法得知左子树与右子树两部分节点的排序关系。
在很多应用场景下,我们不但需要堆的特性,例如快速知道数据最大值或最小值,同时还需要知道元素的排序信息,因此本节我们看看如何实现鱼和熊掌如何兼得。假设我们有一系列数据,它的元素由两部分组成,一部分对应商品的名称,其类型为字符串,一部分对应商品的货存数量,类型为整形,我们既需要将商品根据其名称排序,同时我们又需要快速查询当前货存最小的商品,我们如何设计相应的算法和数据结构来满足这样特性呢。
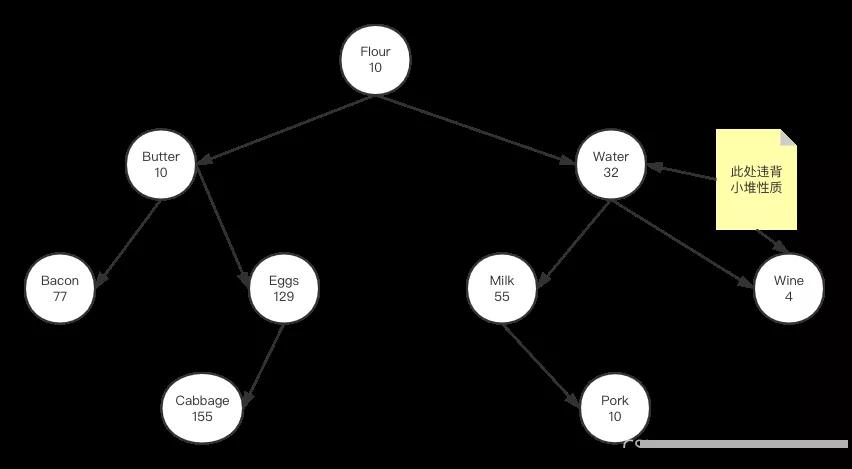
举个例子,如下图:
从上图看,它对应元素字符串是排序二叉树,因此根节点左子树对应元素的字符串都小于根字符串,同时右子树对应的字符串都大于根节点字符串,同时每个元素还对应着相应商品的货存数量,我们需要及时掌握当前货存最少的商品,这样才能在其耗尽之前迅速补货。但是从上图可以看到,要保证字符串的排序性就得牺牲对于商品数量的小堆性质,例如上图中water对应的货存与wine对应的货存违背了小堆的性质,现在问题是如何在保证字符串排序的情况下,确保数量同时能满足小堆性质。
首先我们先定义一下数据结构:
- class Node:
- def __init__(self, key: str, priority: float):
- self._key = key
- self._priority = priority
- self._left: Node = None
- self._right: Node = None
- self._parent: Node = None
- @property
- def left(self):
- return self._left
- @property
- def right(self):
- return self._right
- @property
- def parent(self):
- return self._parent
- @left.setter
- def left(self, node):
- self._left = node
- if node is not None:
- node.parent = self
- @right.setter
- def right(self, node):
- self._right = node
- if node is not None:
- node.parent = self
- @parent.setter
- def parent(self, node):
- self._parent = node
- def is_root(self) -> bool:
- if self.parent is None:
- return True
- return False
- def __repr__(self):
- return "({}, {})".format(self._key, self._priority)
- def __str__(self):
- repr_str: str = ""
- repr_str += repr(self)
- if self.parent is not None:
- repr_str += " parent: " + repr(self.parent)
- else:
- repr_str += " parent: None"
- if self.left is not None:
- repr_str += " left: " + repr(self.left)
- else:
- repr_str += " left: None"
- if self.right is not None:
- repr_str += " right: " + repr(self.right)
- else:
- repr_str += " right: None"
- return repr_str
- class Treap:
- def __init__(self):
- self.root : Node = None
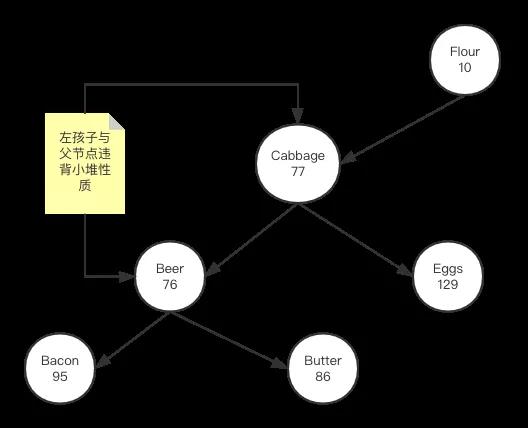
当前问题是,当上图所示的矛盾出现时,我们如何调整,使得字符串依然保持排序性质,同时货存数值能满足小堆性质。我们需要根据几种情况采取不同操作,首先看第一种,如下图:
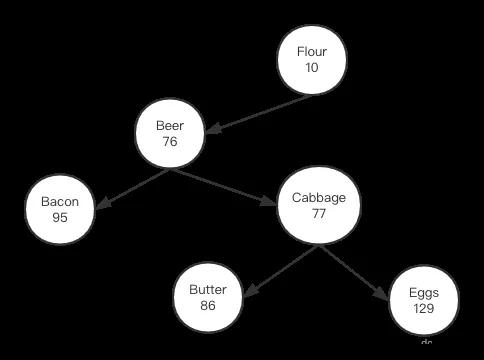
从上图看到,一种情况是父节点与左孩子在数值上违背了堆的性质,此时我们执行一种叫右旋转操作,其步骤是,1,Beer节点逆时针旋转,替换其父节点;2,父节点Cabbage顺时针旋转,成为Beer的右孩子节点;3,原来Beer的右孩子节点转变为Cabbage的左孩子节点;完成后结果如下图所示:
可以看到,此时字符串依然保持排序二叉树性质,同时数值对应的小堆性质也得到了满足。我们看看代码实现:
- class Treap:
- def __init__(self):
- self._root: Node = None
- def right_rotate(self, x: Node):
- if x is None or x.is_root() is True:
- return
- y = x.parent
- if y.left != x: # 必须是左孩子才能右旋转
- return
- p = y.parent
- if p is not None: # 执行右旋转
- if p.left == y:
- p.left = x
- else:
- p.right = x
- else:
- self._root = x
- y.left = x.right
- x.right = y
接下来我们构造一些数据测试一下上面的实现是否正确:
- def setup_right_rotate():
- flour: Node = Node("Flour", 10)
- cabbage: Node = Node("Cabbage", 77)
- beer: Node = Node("Beer", 76)
- bacon: Node = Node("Bacon", 95)
- butter: Node = Node("Butter", 86)
- flour.parent = None
- flour.left = cabbage
- flour.right = None
- cabbage.left = beer
- beer.left = bacon
- beer.right = butter
- return flour, beer
- def print_treap(n: Node):
- if n is None:
- return
- print(n)
- print_treap(n.left)
- print_treap(n.right)
- treap = Treap()
- root, x , cabbage = setup_right_rotate()
- print("---------before right rotate---------:")
- print_treap(root)
- treap.right_rotate(x)
- print("-------after right rotate-------")
- print_treap(root)
上面代码执行后输出内容如下:
- ---------before right rotate---------:
- (Flour, 10) parent: None left: (Cabbage, 77) right: None
- (Cabbage, 77) parent: (Flour, 10) left: (Beer, 76) right: (Eggs, 129)
- (Beer, 76) parent: (Cabbage, 77) left: (Bacon, 95) right: (Butter, 86)
- (Bacon, 95) parent: (Beer, 76) left: None right: None
- (Butter, 86) parent: (Beer, 76) left: None right: None
- (Eggs, 129) parent: (Cabbage, 77) left: None right: None
- -------after right rotate-------
- (Flour, 10) parent: None left: (Beer, 76) right: None
- (Beer, 76) parent: (Flour, 10) left: (Bacon, 95) right: (Cabbage, 77)
- (Bacon, 95) parent: (Beer, 76) left: None right: None
- (Cabbage, 77) parent: (Beer, 76) left: (Butter, 86) right: (Eggs, 129)
- (Butter, 86) parent: (Cabbage, 77) left: None right: None
- (Eggs, 129) parent: (Cabbage, 77) left: None right: None
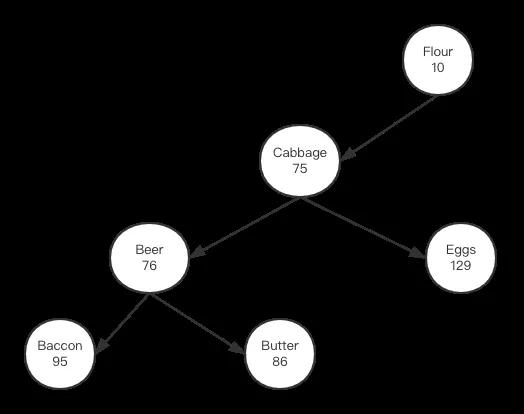
对比右旋转前后输出的二叉树看,旋转后的二叉树打印信息的确跟上面我们旋转后对应的图像是一致的。接下来我们实现左旋转,先把上图中cabbage节点对应的值改成75,这样它与父节点就违背了小堆性质:
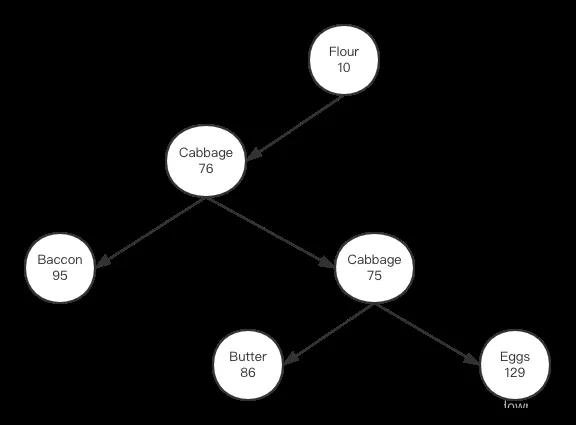
我们要做的是:1,把cabbage节点向“左”旋转到beer的位置;2,beer的父节点设置为cabbage;3:beer的右孩子设置为cabbage的左孩子;4,cabbage的左孩子变成beer;左旋转后二叉树应该成形如下:
从上图看,左旋转后,字符串依然保持二叉树排序性,同时数值的排放也遵守小堆原则,我们看相应的代码实现:
- class Treap:
- ...
- def left_rotate(self, x : Node):
- if x is None or x.is_root() is True:
- return
- y = x.parent
- if y.right is not x: # 只有右孩子才能左旋转
- return
- p = y.parent
- if p is not None:
- if p.left is y:
- p.left = x
- else:
- p.right = x
- else:
- self._root = x
- y.right = x.left
- x.left = y
为了测试上面代码实现,我们首先把cabbage的值修改,然后调用上面代码:
- cabbage._priority = 75
- print("-------before left rotate--------")
- print_treap(root)
- treap.left_rotate(cabbage)
- print("-------after left rotate---------")
- print_treap(root)
代码运行后输出结果为:
- -------before left rotate--------
- (Flour, 10) parent: None left: (Beer, 76) right: None
- (Beer, 76) parent: (Flour, 10) left: (Bacon, 95) right: (Cabbage, 75)
- (Bacon, 95) parent: (Beer, 76) left: None right: None
- (Cabbage, 75) parent: (Beer, 76) left: (Butter, 86) right: (Eggs, 129)
- (Butter, 86) parent: (Cabbage, 75) left: None right: None
- (Eggs, 129) parent: (Cabbage, 75) left: None right: None
- -------after left rotate---------
- (Flour, 10) parent: None left: (Cabbage, 75) right: None
- (Cabbage, 75) parent: (Flour, 10) left: (Beer, 76) right: (Eggs, 129)
- (Beer, 76) parent: (Cabbage, 75) left: (Bacon, 95) right: (Butter, 86)
- (Bacon, 95) parent: (Beer, 76) left: None right: None
- (Butter, 86) parent: (Beer, 76) left: None right: None
- (Eggs, 129) parent: (Cabbage, 75) left: None right: None
输出结果的描述与上图左旋转后的结果是一致的。由于Treap相对于元素的key是排序二叉树,因此在给定一个字符串后,我们很容易查询字符串是否在Treap中,其本质就是排序二叉树的搜索,其实现我们暂时忽略。
虽然查询很简单,但是插入节点则稍微麻烦,因为插入后,新节点与其父节点可能会违背小堆性质,因此在完成插入后,我们还需使用上面实现的左旋转或右旋转来进行调整。