把二叉搜索树转换为累加树
力扣题目:https://leetcode-cn.com/problems/convert-bst-to-greater-tree/
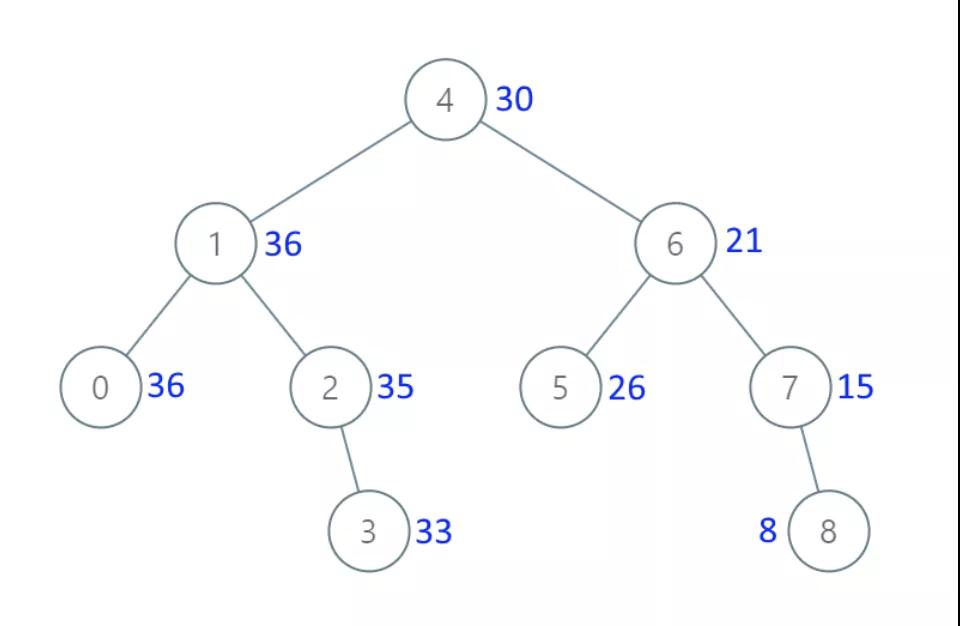
给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束条件:
节点的左子树仅包含键 小于 节点键的节点。节点的右子树仅包含键 大于 节点键的节点。左右子树也必须是二叉搜索树。
示例 1:
把二叉搜索树转换为累加树
- 输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
- 输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
示例 2:
- 输入:root = [0,null,1]
- 输出:[1,null,1]
示例 3:
- 输入:root = [1,0,2]
- 输出:[3,3,2]
示例 4:
- 输入:root = [3,2,4,1]
- 输出:[7,9,4,10]
提示:
- 树中的节点数介于 0 和 104 之间。
- 每个节点的值介于 -104 和 104 之间。
- 树中的所有值 互不相同 。
- 给定的树为二叉搜索树。
思路
一看到累加树,相信很多小伙伴都会疑惑:如何累加?遇到一个节点,然后在遍历其他节点累加?怎么一想这么麻烦呢。
然后再发现这是一颗二叉搜索树,二叉搜索树啊,这是有序的啊。
那么有序的元素如果求累加呢?
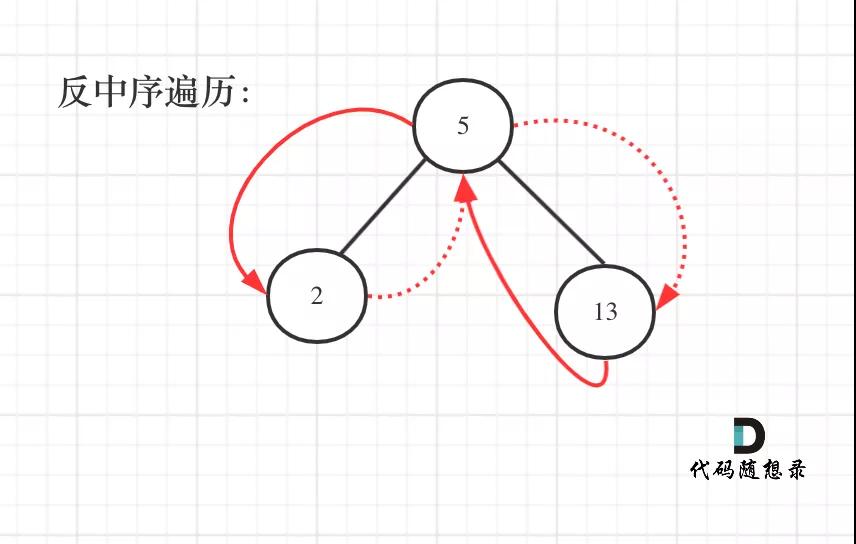
其实这就是一棵树,大家可能看起来有点别扭,换一个角度来看,这就是一个有序数组[2, 5, 13],求从后到前的累加数组,也就是[20, 18, 13],是不是感觉这就简单了。
为什么变成数组就是感觉简单了呢?
因为数组大家都知道怎么遍历啊,从后向前,挨个累加就完事了,这换成了二叉搜索树,看起来就别扭了一些是不是。
那么知道如何遍历这个二叉树,也就迎刃而解了,从树中可以看出累加的顺序是右中左,所以我们需要反中序遍历这个二叉树,然后顺序累加就可以了。
递归
遍历顺序如图所示:
把二叉搜索树转换为累加树
本题依然需要一个pre指针记录当前遍历节点cur的前一个节点,这样才方便做累加。
pre指针的使用技巧,我们在二叉树:搜索树的最小绝对差和二叉树:我的众数是多少?都提到了,这是常用的操作手段。
递归函数参数以及返回值
这里很明确了,不需要递归函数的返回值做什么操作了,要遍历整棵树。
同时需要定义一个全局变量pre,用来保存cur节点的前一个节点的数值,定义为int型就可以了。
代码如下:
int pre; // 记录前一个节点的数值
void traversal(TreeNode* cur)
- 1.
- 2.
- 确定终止条件
遇空就终止。
if (cur == NULL) return;
- 1.
- 确定单层递归的逻辑
注意要右中左来遍历二叉树, 中节点的处理逻辑就是让cur的数值加上前一个节点的数值。
代码如下:
traversal(cur->right); // 右
cur->val += pre; // 中
pre = cur->val;
traversal(cur->left); // 左
- 1.
- 2.
- 3.
- 4.
递归法整体代码如下:
class Solution {
private:
int pre; // 记录前一个节点的数值
void traversal(TreeNode* cur) { // 右中左遍历
if (cur == NULL) return;
traversal(cur->right);
cur->val += pre;
pre = cur->val;
traversal(cur->left);
}
public:
TreeNode* convertBST(TreeNode* root) {
pre = 0;
traversal(root);
return root;
}
};
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
迭代法
迭代法其实就是中序模板题了,在二叉树:前中后序迭代法和二叉树:前中后序统一方式迭代法可以选一种自己习惯的写法。
这里我给出其中的一种,代码如下:
class Solution {
private:
int pre; // 记录前一个节点的数值
void traversal(TreeNode* root) {
stack<TreeNode*> st;
TreeNode* cur = root;
while (cur != NULL || !st.empty()) {
if (cur != NULL) {
st.push(cur);
cur = cur->right; // 右
} else {
cur = st.top(); // 中
st.pop();
cur->val += pre;
pre = cur->val;
cur = cur->left; // 左
}
}
}
public:
TreeNode* convertBST(TreeNode* root) {
pre = 0;
traversal(root);
return root;
}
};
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
总结
经历了前面各种二叉树增删改查的洗礼之后,这道题目应该比较简单了。
好了,二叉树已经接近尾声了,接下来就是要对二叉树来一个大总结了。
其他语言版本
Java
class Solution {
int sum;
public TreeNode convertBST(TreeNode root) {
sum = 0;
convertBST1(root);
return root;
}
// 按右中左顺序遍历,累加即可
public void convertBST1(TreeNode root) {
if (root == null) {
return;
}
convertBST1(root.right);
sum += root.val;
root.val = sum;
convertBST1(root.left);
}
}
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
Python
递归法
class Solution:
def convertBST(self, root: TreeNode) -> TreeNode:
def buildalist(root):
if not root: return None
buildalist(root.right) #右中左遍历
root.val += self.pre
self.pre = root.val
buildalist(root.left)
self.pre = 0 #记录前一个节点的数值
buildalist(root)
return root
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
本文转载自微信公众号「代码随想录」,可以通过以下二维码关注。转载本文请联系代码随想录公众号。