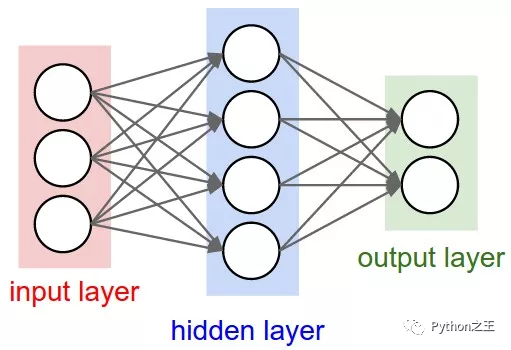
多层感知机(MLP)有着非常悠久的历史,多层感知机(MLP)是深度神经网络(DNN)的基础算法
MLP基础知识
- 目的:创建用于简单回归/分类任务的常规神经网络(即多层感知器)和Keras
MLP结构
- 每个MLP模型由一个输入层、几个隐藏层和一个输出层组成
- 每层神经元的数目不受限制
具有一个隐藏层的MLP
- 输入神经元数:3 - 隐藏神经元数:4 - 输出神经元数:2
回归任务的MLP
- 当目标(「y」)连续时
- 对于损失函数和评估指标,通常使用均方误差(MSE)
- from tensorflow.keras.datasets import boston_housing
- (X_train, y_train), (X_test, y_test) = boston_housing.load_data()
数据集描述
- 波士顿住房数据集共有506个数据实例(404个培训和102个测试)
- 13个属性(特征)预测“某一地点房屋的中值”
- 文件编号:https://keras.io/datasets/
1.创建模型
- Keras模型对象可以用Sequential类创建
- 一开始,模型本身是空的。它是通过「添加」附加层和编译来完成的
- 文档:https://keras.io/models/sequential/
- from tensorflow.keras.models import Sequential
- model = Sequential()
1-1.添加层
- Keras层可以「添加」到模型中
- 添加层就像一个接一个地堆叠乐高积木
- 文档:https://keras.io/layers/core/
- from tensorflow.keras.layers import Activation, Dense
- # Keras model with two hidden layer with 10 neurons each
- model.add(Dense(10, input_shape = (13,))) # Input layer => input_shape should be explicitly designated
- model.add(Activation('sigmoid'))
- model.add(Dense(10)) # Hidden layer => only output dimension should be designated
- model.add(Activation('sigmoid'))
- model.add(Dense(10)) # Hidden layer => only output dimension should be designated
- model.add(Activation('sigmoid'))
- model.add(Dense(1)) # Output layer => output dimension = 1 since it is regression problem
- # This is equivalent to the above code block
- model.add(Dense(10, input_shape = (13,), activation = 'sigmoid'))
- model.add(Dense(10, activation = 'sigmoid'))
- model.add(Dense(10, activation = 'sigmoid'))
- model.add(Dense(1))
1-2.模型编译
- Keras模型应在培训前“编译”
- 应指定损失类型(函数)和优化器
- 文档(优化器):https://keras.io/optimizers/
- 文档(损失):https://keras.io/losses/
- from tensorflow.keras import optimizers
- sgd = optimizers.SGD(lr = 0.01) # stochastic gradient descent optimizer
- model.compile(optimizer = sgd, loss = 'mean_squared_error', metrics = ['mse']) # for regression problems, mean squared error (MSE) is often employed
模型摘要
- model.summary()
- odel: "sequential"
- _________________________________________________________________
- Layer (type) Output Shape Param #
- =================================================================
- dense (Dense) (None, 10) 140
- _________________________________________________________________
- activation (Activation) (None, 10) 0
- _________________________________________________________________
- dense_1 (Dense) (None, 10) 110
- _________________________________________________________________
- activation_1 (Activation) (None, 10) 0
- _________________________________________________________________
- dense_2 (Dense) (None, 10) 110
- _________________________________________________________________
- activation_2 (Activation) (None, 10) 0
- _________________________________________________________________
- dense_3 (Dense) (None, 1) 11
- _________________________________________________________________
- dense_4 (Dense) (None, 10) 20
- _________________________________________________________________
- dense_5 (Dense) (None, 10) 110
- _________________________________________________________________
- dense_6 (Dense) (None, 10) 110
- _________________________________________________________________
- dense_7 (Dense) (None, 1) 11
- =================================================================
- Total params: 622
- Trainable params: 622
- Non-trainable params: 0
- _________________________________________________________________
2.培训
- 使用提供的训练数据训练模型
- model.fit(X_train, y_train, batch_size = 50, epochs = 100, verbose = 1)
3.评估
- Keras模型可以用evaluate()函数计算
- 评估结果包含在列表中
- 文档:https://keras.io/metrics/
- results = model.evaluate(X_test, y_test)
- print(model.metrics_names) # list of metric names the model is employing
- print(results) # actual figure of metrics computed
- print('loss: ', results[0])
- print('mse: ', results[1])