每日算法：字符串相乘-字符串计算

本文转载自微信公众号「三分钟学前端」，作者sisterAn。转载本文请联系三分钟学前端公众号。

给定两个以字符串形式表示的非负整数 num1 和 num2，返回 num1 和 num2 的乘积，它们的乘积也表示为字符串形式。

示例 1:

输入: num1 = "2", num2 = "3" 
输出: "6" 
1.
2.

示例 2:

输入: num1 = "123", num2 = "456" 
输出: "56088" 
1.
2.

说明：

num1 和 num2 的长度小于110。
num1 和 num2 只包含数字 0-9。
num1 和 num2 均不以零开头，除非是数字 0 本身。
不能使用任何标准库的大数类型(比如 BigInteger)或直接将输入转换为整数来处理。

解法一：常规解法

从右往左遍历乘数，将乘数的每一位与被乘数相乘得到对应的结果，再将每次得到的结果累加

另外，当乘数的每一位与被乘数高位(非最低位)相乘的时候，注意低位补 '0'

let multiply = function(num1, num2) { 
    if (num1 === "0" || num2 === "0") return "0" 
     
    // 用于保存计算结果 
    let res = "0" 
         
    // num2 逐位与 num1 相乘 
    for (let i = num2.length - 1; i >= 0; i--) { 
        let carry = 0 
        // 保存 num2 第i位数字与 num1 相乘的结果 
        let temp = '' 
        // 补 0  
        for (let j = 0; j < num2.length - 1 - i; j++) { 
            temp+='0' 
        } 
        let n2 = num2.charAt(i) - '0' 
             
        // num2 的第 i 位数字 n2 与 num1 相乘 
        for (let j = num1.length - 1; j >= 0 || carry != 0; j--) { 
            let n1 = j < 0 ? 0 : num1.charAt(j) - '0' 
            let product = (n1 * n2 + carry) % 10 
            temp += product  
            carry = Math.floor((n1 * n2 + carry) / 10) 
        } 
        // 将当前结果与新计算的结果求和作为新的结果 
        res = addStrings(res, Array.prototype.slice.call(temp).reverse().join("")) 
    } 
    return res 
} 
 
let addStrings = function(num1, num2) { 
    let a = num1.length, b = num2.length, result = '', tmp = 0 
    while(a || b) { 
        a ? tmp += +num1[--a] : '' 
        b ? tmp +=  +num2[--b] : '' 
         
        result = tmp % 10 + result 
        if(tmp > 9) tmp = 1 
        else tmp = 0 
    } 
    if (tmp) result = 1 + result 
    return result 
} 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.

复杂度分析：

时间复杂度：O(max(m*n , n * n))
空间复杂度：O(m+n)

解法二：竖式相乘(优化)

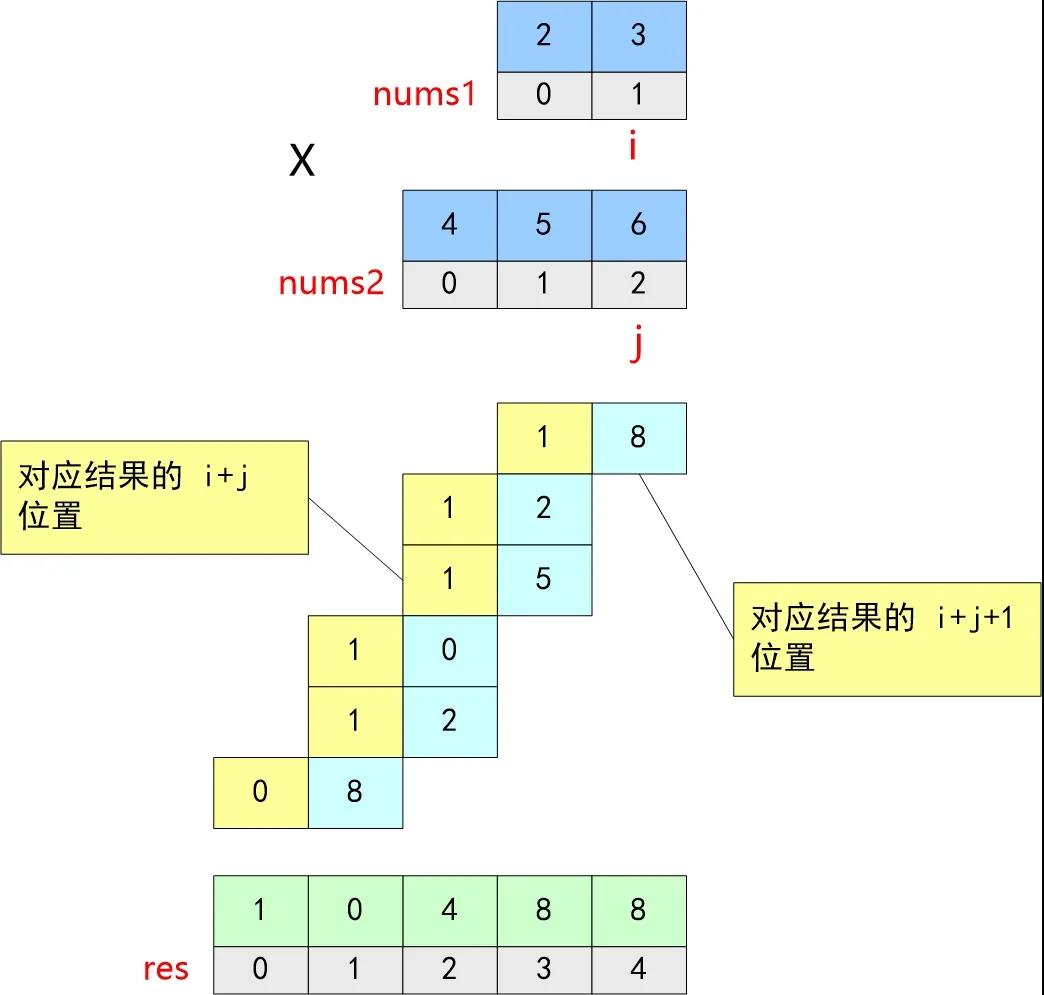
两个数M和N相乘的结果可以由 M 乘上 N 的每一位数的和得到，如下图所示：

计算 num1 依次乘上 num2 的每一位的和
把得到的所有和按对应的位置累加在一起，就可以得到 num1 * num2 的结果

let multiply = function(num1, num2) { 
    if(num1 === '0' || num2 === '0') return "0" 
     
    // 用于保存计算结果 
    let res = [] 
     
    // 从个位数开始逐位相乘 
    for(let i = 0 ; i < num1.length; i++){ 
        // num1 尾元素 
        let tmp1 = +num1[num1.length-1-i] 
         
        for(let j = 0; j < num2.length; j++){ 
            // num2尾元素 
            let tmp2 = +num2[num2.length-1-j] 
             
            // 判断结果集索引位置是否有值 
            let pos = res[i+j] ? res[i+j]+tmp1*tmp2 : tmp1*tmp2 
            // 赋值给当前索引位置 
            res[i+j] = pos%10 
            // 是否进位 这样简化res去除不必要的"0" 
            pos >=10 && (res[i+j+1]=res[i+j+1] ? res[i+j+1]+Math.floor(pos/10) : Math.floor(pos/10)); 
        } 
    } 
    return res.reverse().join(""); 
} 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.

复杂度分析：

时间复杂度：O(m * n)
空间复杂度：O(m + n)