基数排序的1个小技巧，2种排序方式，3种排序算法

[[421174]]

基数排序

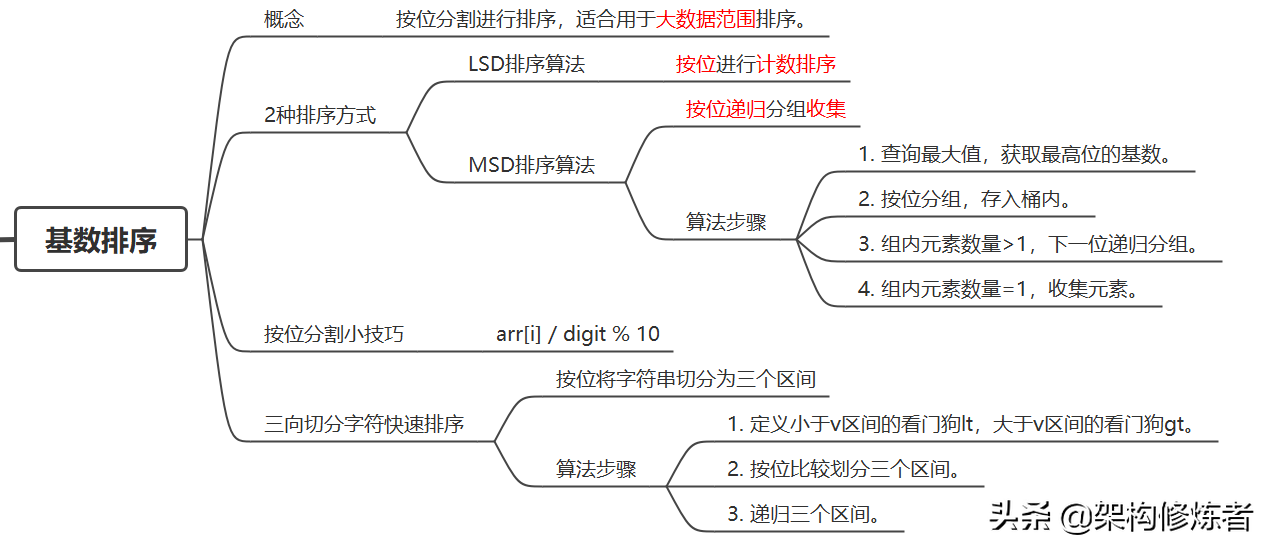
概念

基数排序是非比较型整数排序算法，其原理是将整数按位分割进行排序。基数排序适用于大范围数据排序，打破了计数排序的限制。由于整数也可以表达字符串(比如名字或日期)和特定格式的浮点数，所以基数排序也不是只能使用于整数。

2种排序方式

最低位优先法(LSD)：从最低位向最高位依次按位进行排序。

最高位优先法(MSD)：从最高位向最低位依次按位进行排序。

按位分割小技巧

arr[i] / digit % 10，其中digit为10^n。

LSD排序算法实现

算法思想

按位进行计数排序

算法实现代码

/** 
     * 按位进行计数排序 
     * @param arr 
     * @param divid 
     * @return 
     */ 
private static int[] countingSort(int[] arr, int divid){ 
 
    int[] bucket = new int[10]; 
    for (int i = 0; i < arr.length; i++) { 
        bucket[arr[i] / divid % 10]++; 
    } 
 
    for (int i = 1; i < bucket.length; i++) { 
        bucket[i] = bucket[i-1] + bucket[i]; 
    } 
 
    int[] sortArr = new int[arr.length]; 
    for (int i = arr.length - 1; i >= 0; i--){ 
        int position = bucket[arr[i] / divid % 10]; 
        sortArr[position - 1] = arr[i]; 
        bucket[arr[i] / divid % 10]--; 
    } 
    return sortArr; 
} 
 
public static int[] radixSort(int[] arr) { 
    // 查找数组最大值 
    int max = arr[0]; 
    for (int i = 0; i < arr.length; i++) { 
        max = Math.max(arr[i], max); 
    } 
    // 按位排序 
    int digit = 1; 
    for (int i = 1; i < max; digit*=10, i = digit) { 
        arr = countingSort(arr, digit); 
    } 
    return arr; 
} 

排序验证：

public static void main(String[] args) { 
     int[] arr = {999,1000,1001,1000,999,1005}; 
     System.out.println("排序前:" + JSON.toJSONString(arr)); 
     int[] sortArr = radixSort(arr); 
     System.out.println("排序后:" + JSON.toJSONString(sortArr)); 
 } 

排序前:[999,1000,1001,1000,999,1005] 排序后:[999,999,1000,1000,1001,1005]

MSD排序算法实现

算法思想

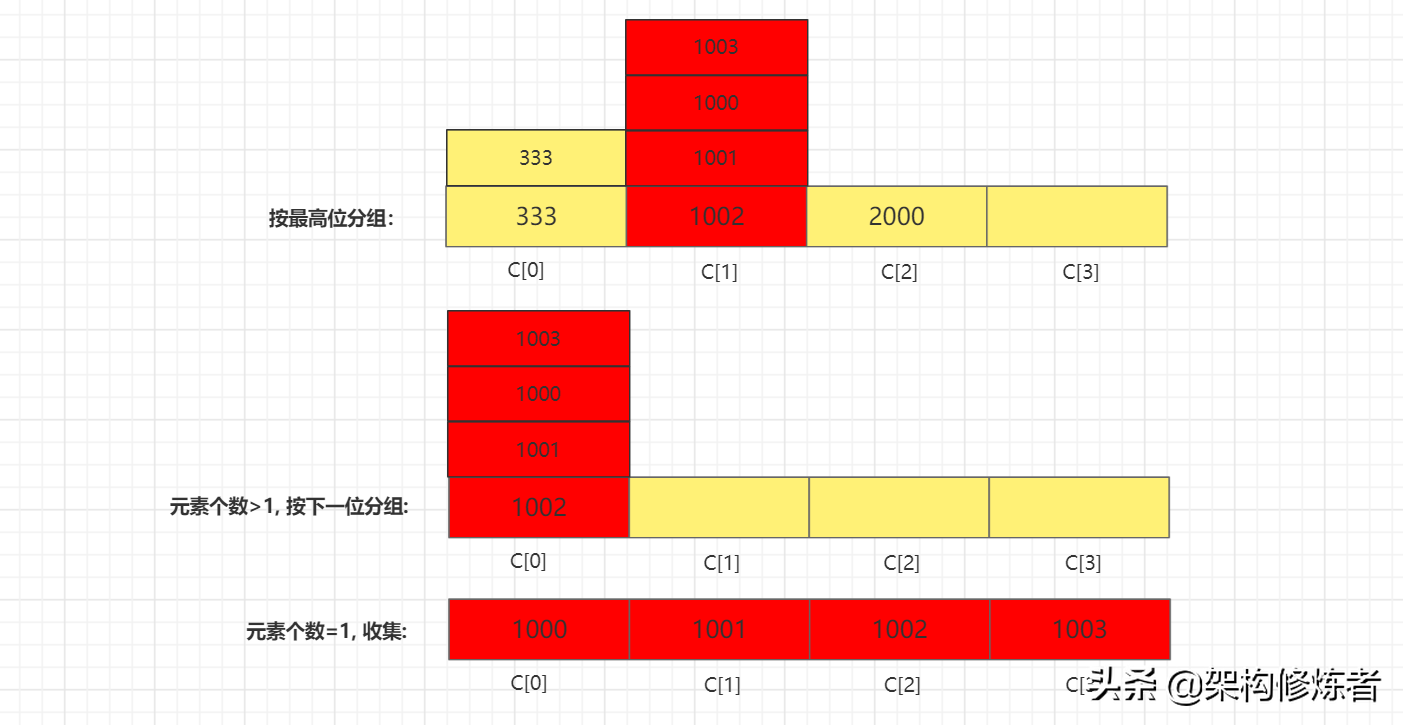
从最高位开始，按位分组，当组内元素个数>1时，递归下一位分组，一直分到个位结束;收集元素个数=1的。

算法步骤

• 查询最大值，获取最高位的基数。Math.pow(10, digit - 1)
• 按位分组，存入桶内。groupBucket[position][groupCounter[position]] =arr[i];
• 组内元素数量>1，下一位递归分组。if (groupBucket[i] > 1) {int[] tmp = msdSort(copyArr, radix / 10);}
• 组内元素数量=1，收集元素。sortArr[index++] = groupBucket[i][0];

比如，对数组[333,1002,1001,1000,333,1003,2000]进行排序，操作步骤如下：

算法实现代码

public static int[] sort(int[] arr){ 
 
    int max = arr[0]; 
    for (int i = 0; i < arr.length; i++) { 
        // 获取最大值 
        max = Math.max(arr[i], max); 
    } 
 
    // 获取最大值的位数 
    int digit = getDataDigit(max); 
    // 计算最大值的基数 
    int radix = new Double(Math.pow(10, digit - 1)).intValue(); 
    // msd基数排序 
    return msdSort(arr, radix); 
} 
 
/** 
     * MSD 基数排序 
     * @param arr 
     * @param radix 
     * @return 
     */ 
public static int[] msdSort(int[] arr, int radix){ 
 
    // 递归分组到个位，退出 
    if (radix <= 0) { 
        return arr; 
    } 
 
    // 分组计数器 
    int[] groupCounter = new int[10]; 
    // 分组桶 
    int[][] groupBucket = new int[10][arr.length]; 
    // 遍历待排序数组，按位分组 
    for (int i = 0; i < arr.length; i++) { 
        // 计算分组桶位置 
        int position = arr[i] / radix % 10; 
        // 将元素存入分组 
        groupBucket[position][groupCounter[position]] = arr[i]; 
        // 当前分组计数加1 
        groupCounter[position]++; 
    } 
 
    int index = 0; 
    int[] sortArr = new int[arr.length]; 
 
    // 遍历分组计数器 
    for (int i = 0; i < groupCounter.length; i++) { 
        // 组内元素数量>1，递归分组 
        if (groupCounter[i] > 1) { 
            int[] copyArr = Arrays.copyOf(groupBucket[i], groupCounter[i]); 
            // 递归分组 
            int[] tmp = msdSort(copyArr, radix / 10); 
            // 收集递归分组后的元素 
            for (int j = 0; j < tmp.length; j++) { 
                sortArr[index++] = tmp[j]; 
            } 
        } else if (groupCounter[i] == 1) { 
            // 收集组内元素数量=1的元素 
            sortArr[index++] = groupBucket[i][0]; 
        } 
    } 
 
    return sortArr; 
} 
 
/** 
     * 获取数据的位数 
     * @param data 
     * @return 
     */ 
public static int getDataDigit(int data) { 
    //        int index = 0; 
    //        int digit = 1; 
    //        while (data / digit >0) { 
    //            digit *= 10; 
    //            index++; 
    //        } 
    //        return index; 
 
    return String.valueOf(data).length(); 
} 

验证排序结果：

public static void main(String[] args) { 
    int[] arr = {333,1002,1001,1000,333,1003,2000}; 
    System.out.println("排序前:" + JSON.toJSONString(arr)); 
    int[] sortArr = sort(arr); 
    System.out.println("排序后:" + JSON.toJSONString(sortArr)); 
} 

排序前:[333,1002,1001,1000,333,1003,2000] 排序后:[333,333,1000,1001,1002,1003,2000]

三向切分字符快速排序

算法思想

按位将字符串切分为三个区间，小于v区间：[lo,lt-1]，等于v区间：[lt,gt]，大于v区间: [gt+1,hi]，依次递归三个区间。

算法步骤

• 定义小于v区间的看门狗lt，大于v区间的看门狗gt。
• 按位比较划分三个区间。
• 递归三个区间。

算法实现代码

/** 
     * 按位将字符串切分为三个区间 
     * 1. 小于v区间：[lo,lt] 
     * 2. 等于v区间：[lt,gt] 
     * 3. 大于v区间: [gt+1,hi] 
     * @param arr 
     * @param lo 
     * @param hi 
     * @param d 
     */ 
public static void sortStr(String[] arr, int lo, int hi, int d){ 
    if (hi <= lo) { 
        return; 
    } 
    // 定义小于v的看门lt, 大于v的看门gt 
    int lt = lo, gt = hi, i = lo + 1, v = charAt(arr[lo],d); 
    while (i <= gt){ 
        int t = charAt(arr[i], d); 
        if (t < v) { 
            exch(arr, i++, lt++); 
        } else if (t > v) { 
            exch(arr, i, gt--); 
        } else { 
            i++; 
        } 
    } 
 
    // 递归小于v的区间 
    sortStr(arr, lo, lt - 1, d); 
    // 递归等于v的区间 
    if (v >= 0) { 
        sortStr(arr, lt, gt, d + 1); 
    } 
    // 递归大于v的区间 
    sortStr(arr, gt + 1, hi, d); 
} 
private static int charAt(String s, int d) { 
    if (d < s.length()) { 
        return s.charAt(d); 
    } 
    return -1; 
} 
public static void exch(String[] arr, int sourceIdx, int targetIdx) { 
    String tmp = arr[sourceIdx]; 
    arr[sourceIdx] = arr[targetIdx]; 
    arr[targetIdx] = tmp; 
} 
结果验证： 
 
 public static void main(String[] args) { 
     String[] a = new String[]{"by","air","she","shell","the","okay","bump","shirt","shells","sh","the","shells","the"}; 
     System.out.println("排序前:" + JSON.toJSONString(a)); 
     sortStr(a, 0, a.length - 1, 0); 
     System.out.println("排序后:" + JSON.toJSONString(a)); 
 } 

排序前:["by","air","she","shell","the","okay","bump","shirt","shells","sh","the","shells","the"] 排序后:["air","bump","by","okay","sh","she","shell","shells","shells","shirt","the","the","the"]

三种排序算法对比

总结

基数排序是稳定、非比较排序，适合用于大数据范围的。