面试官:我们继续来聊聊关于数据结构与算法,你能写一个快速排序?(说话的同时,把我简历反过来,递给我一支笔,意思就是叫我在自己的简历背后写)
菜鸟我:什么意思?这里写吗?(指着简历)
面试官:嗯
菜鸟我:不会
面试官:好吧,今天面试就到这里
菜鸟我:(心里很火,劳资的简历,想在劳资简历上写代码?)沙雕
面试官:(回头看了一眼,一脸懵逼)
想想自己还是太年轻了,换着是现在就不是这样了。写就写嘛,反正不就是一张纸而已。图片
其实,快排说简单嘛,估计很多人也手写不出来,说难吗也有很多人你能现场手写几种方式。
菜鸟我,当年还是能手写一种,毕竟面试前我刚好刻意的准备过“默写快排”。
下面,我们就来分析分析----快速排序。
背景
来自百科:
快速排序由C. A. R. Hoare在1962年提出。它的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以[递归]进行,以此达到整个数据变成有序序列。
这概念理解起来 还是蛮费劲儿的。
可以这么理解:
快速排序是冒泡排序的改进版,整个过程就在拆拆补补,东拆西补或西拆东补,一边拆一边补,直到所有元素达到有序状态。
核心思想:
先从数列中取出一个数作为基准数,然后进行大小分区;
分区过程,将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边;
再对左右区间重复第二步,直到各区间只有一个数,排序完成。
实现案例
下面先通过图文形式一步一步进行拆解。
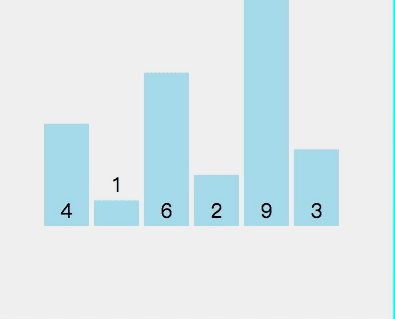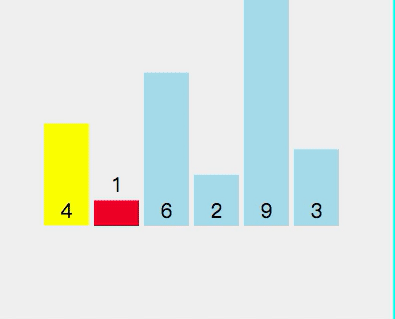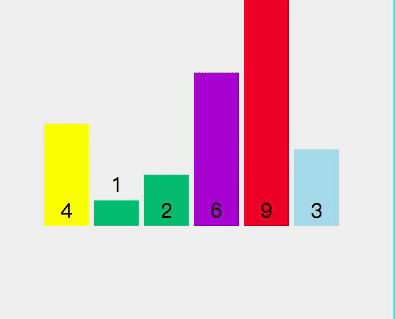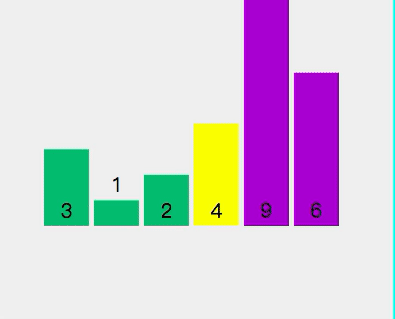
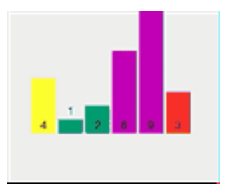
拿[4,1,6,2,9,3]这个数组举例。
第一遍遍历:
- 先进行拆分 [4,1,6,2,9,3] 选择元素 4 作为轴心点
- 检查是否 1 < 4 (轴心点)
- 检查是否 6 < 4 (轴心点)
- 检查是否 2 < 4 (轴心点)
- 2 < 4 (轴心点) 是为真,将指数2和 存储指数 6 进行交换
- 检查是否 9 < 4 (轴心点)
- 检查是否 3 < 4 (轴心点)
- 3 < 4 (轴心点) 为真,将指数3和存储指数6 进行交换
- 将轴心点4和存储指数3进行交换
- 此时轴心点4左边全部小于4,右边大于4
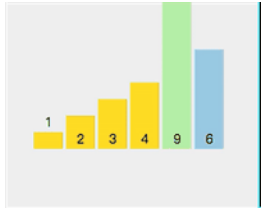
目前数组顺序为[3,1,2,4,9,6]。
下一步:
- 先将左边先排好序
- 选择元素 3 作为轴心点
- 检查是否 1 < 3 (轴心点)
- 检查是否 2 < 3 (轴心点)
- 将轴心点 3和存储指数值 2进行交换
- 现在轴心点已经在排序过后的位置
- 进行拆分 [2,1] 选择 2 作为轴心点
- 检查是否 1 < 2 (轴心点)
- 左边遍历完成,将轴心点2和存储指数1 进行交换
右边同理……避免视觉疲劳就不一一描述了,可看下面动态演示图。
2. 快速排序法全流程
3.代码实现
下面,我们使用Java语言来实现前面的快排案例:
- import java.util.Arrays;
- public class QuickSortDemo {
- //四个步骤:
- //1.比较startIndex和endIndex,更喜欢理解为校验
- //2.找出基准
- //3.左边部分排序
- //4.右边排序
- public static void quickSort(int[] arr, int startIndex, int endIndex) {
- if (startIndex < endIndex) {
- //找出基准
- int partition = partition(arr, startIndex, endIndex);
- //分成两边递归进行
- quickSort(arr, startIndex, partition - 1);
- quickSort(arr, partition + 1, endIndex);
- }
- }
- //找基准
- private static int partition(int[] arr, int startIndex, int endIndex) {
- int pivot = arr[startIndex];
- int left = startIndex;
- int right = endIndex;
- //等于就没有必要排序
- while (left != right) {
- while (left < right && arr[right] > pivot) {
- right--;
- }
- while (left < right && arr[left] <= pivot) {
- left++;
- }
- //找到left比基准大,right比基准小,进行交换
- if (left < right) {
- swap(arr, left, right);
- }
- }
- //第一轮完成,让left和right重合的位置和基准交换,返回基准的位置
- swap(arr, startIndex, left);
- return left;
- }
- //两数交换
- public static void swap(int[] arr, int i, int j) {
- int temp = arr[i];
- arr[i] = arr[j];
- arr[j] = temp;
- }
- public static void main(String[] args) {
- int[] a = {3, 1, 2, 4, 9, 6};
- quickSort(a, 0, a.length - 1);
- //输出结果
- System.out.println(Arrays.toString(a));
- }
- }
输出结果:
- [1, 2, 3, 4, 6, 9]
代码实现,建议结合前面的动图,理解起来就更简单了。
快排写法还有几种,感兴趣的可以自行查找一下,另外也可以看看维基百科中,快排是怎么介绍的。
4.复杂度分析
时间复杂度:
最坏情况就是每一次取到的元素就是数组中最小/最大的,这种情况其实就是冒泡排序了(每一次都排好一个元素的顺序)
这种情况时间复杂度就好计算了,就是冒泡排序的时间复杂度:T[n] = n * (n-1) = n^2 + n;
最好情况下是O(nlog2n),推导过程如下:
(递归算法的时间复杂度公式:T[n] = aT[n/b] + f(n) )
https://img2018.cnblogs.com/blog/1258817/201903/1258817-20190326191158640-601403776.png
所以平均时间复杂度为O(nlog2n)
空间复杂度:
快速排序使用的空间是O(1)的,也就是个常数级;而真正消耗空间的就是递归调用了,因为每次递归就要保持一些数据:
最优的情况下空间复杂度为:O(log2n);每一次都平分数组的情况
最差的情况下空间复杂度为:O( n );退化为冒泡排序的情况
所以平均空间复杂度为O(log2n)
5. 快速排序法总结
默认取第一个元素为轴心点(轴心点的确认区分了 “快速排序法”和“随机排序法”)两种算法,而随机排序则随机rand一个元素为轴心点;
如果两个不相邻元素交换,可以一次交换消除多个逆序,加快排序进程。
后记
最后再说说,其实你觉得快速排序在工作中有用吗?工作近十年的我真的没用过,但我知道这个快排的思路。如果面试前不准备,我反正是肯定写不出来的,你呢?