01故事起源
有一个容量有限的背包,容量为w,以及m个待选择的物品,每个只有一件。每个物品有一定的重量和价值,那么选择哪些物品放入背包,可使选择的物品总价值最大呢?
02问题解析
如果背包没有容量限制,那肯定是把所有的物品都放入背包可使价值最大。
但现在背包比较小,只能选择部分装进背包,比如只能放一个,那就把钻石装进去。
很容易可以想到,尽量放重量小且单价高的物品,但怎么对问题进行一个严谨的建模呢,继续往下分析。
03分析
背包有一个固定的容量,容量是1kg,或者2kg,或者3kg,其实具体的数量对问题的本质没有影响。
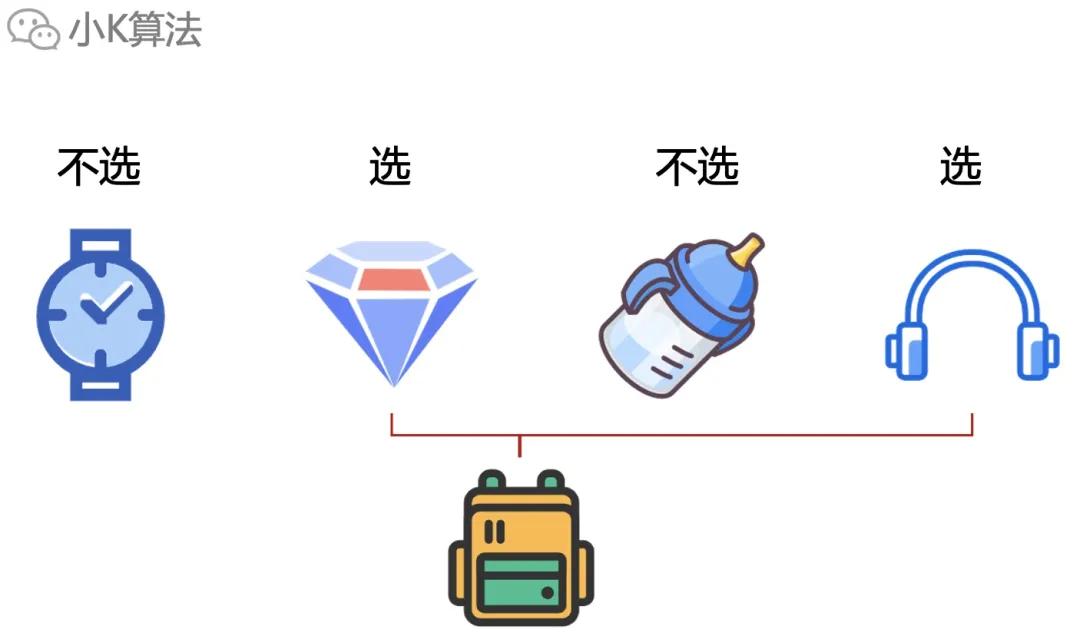
对于物品来说,也就分两种情况,要么放入背包,要么不放。
有m个物品,那总共就有2^m种选择方式,很明显这个数量很大,所以也不可能直接把所有的选择方式枚举出来。
04小问题过度大问题
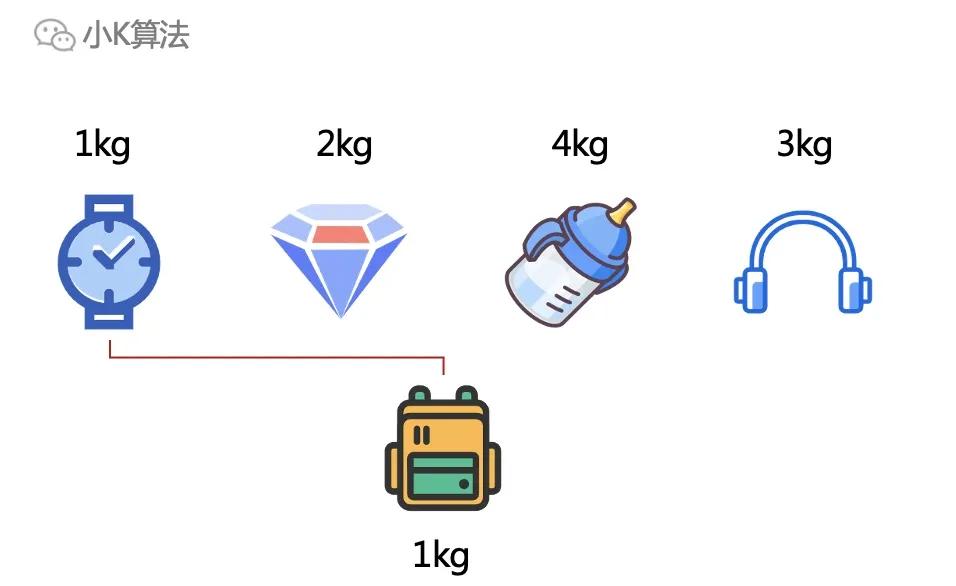
假设背包容量为1kg,那可装入的最大价值就是将手表装入,其他的也装不下。
如果有一个更大的背包,它的容量可以看成是2个小容量的背包的总和。
但它能装入的价值却不能简单的直接分解为2个小背包,因为物品只有一个,这会导致物品重复。
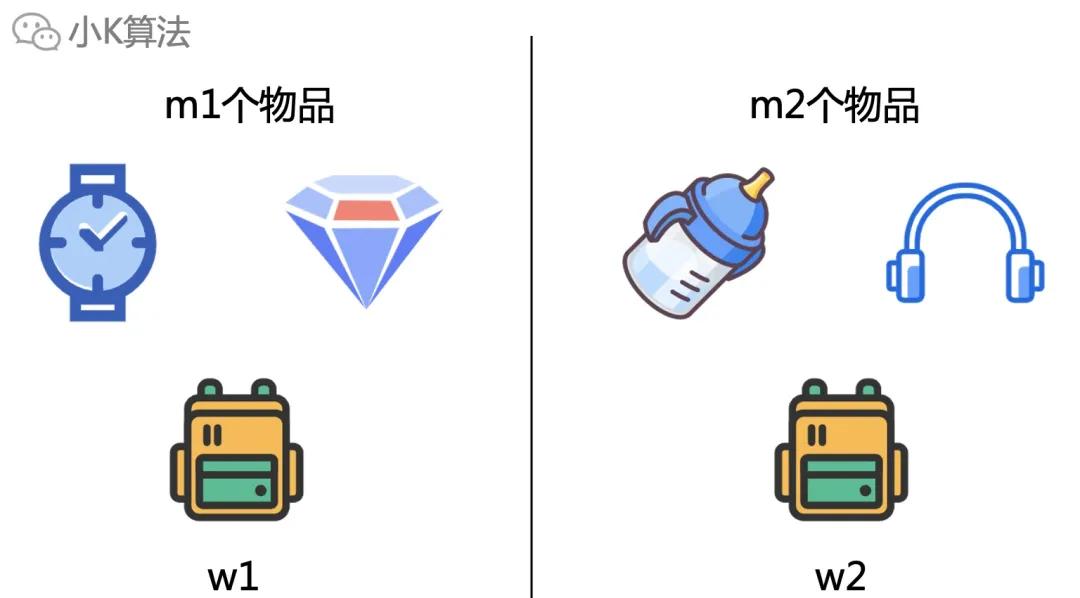
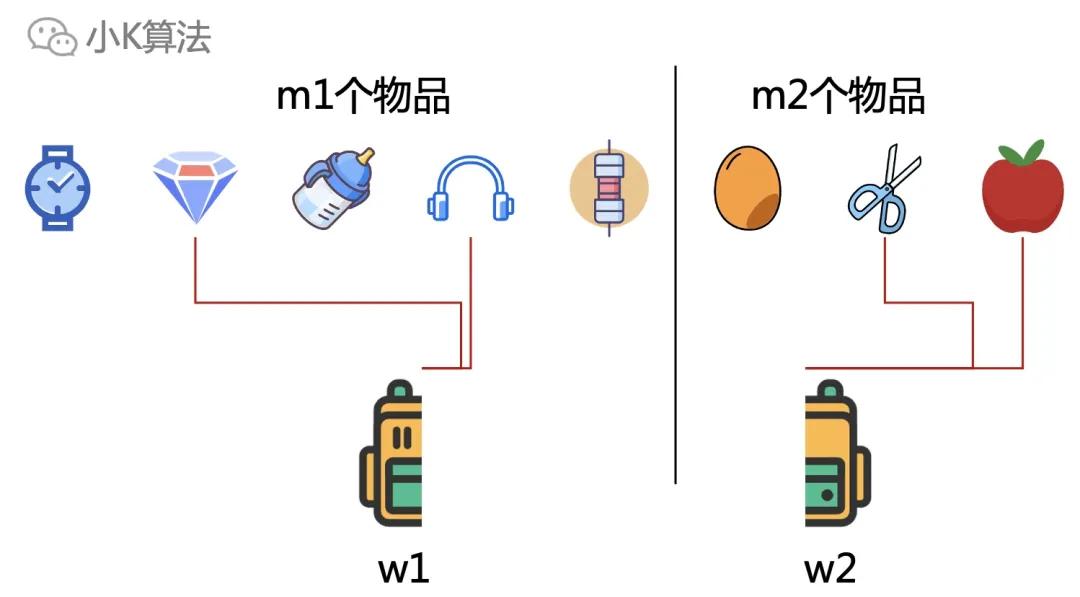
所以对物品也再进行一次划分,m个物品可以分解为m1+m2个,同时背包容量也分解为w1+w2。
再看上面左右两边,和原来的问题还是一样的,本质不变,只是变成了数据规模更小的一个子问题。如果有了子问题的答案,那是不是就可以组合成更大规模的答案了呢?
我猜这里肯定有同学会说,这样分解的小问题一定能得到最终大问题的最优解吗?我们来尝试证明一下。
05逆向思维
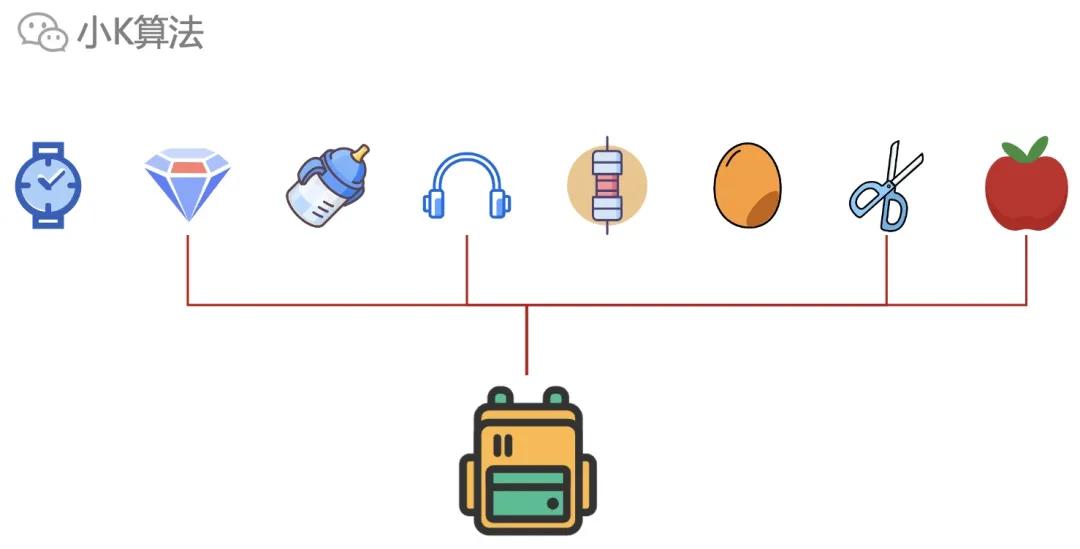
假设下面就是最终的最优解选择的物品。
如果从某个位置砍一刀分开,保证w1和w2能装下自己这边的最终选择物品,那最优解也就被分成了两个小规模问题的最优解。这也说明如果枚举了所有小规模最优解的组合方式,也一定能得到大规模的最优解。
06算法建模
根据上面的分析,现在问题就变得简单了,直接按物品和重量拆分小问题,通过小问题递推出大问题就行了。
设f[i][j]表示前i个物品背包容量为j时,能选择的最大价值。w[i]表示第i个物品的重量,v[i]表示第i个物品的价值。
- 装不下第i个物品,则f[i][j]=f[i-1][j]
- 能装下第i个物品,则f[i][j]=max(f[i][j],f[i-1][j-w[i]]+v[i])
那为什么只需要从前i-1个物品递推就行了呢,因为只需要有一种情况能得到最优解就够了,并不需要把前面的所有划分都枚举出来。这其实就相当于把i个物品划分成i-1个物品和1个物品时的情况。前面的子问题也已经包含在当前的解中了。
代码实现
- int f[101][1001], w[101], v[101];
- int n, m;
- int main() {
- cin >> m >> n;
- for (int i = 1; i <= m; ++i) {
- cin >> w[i] >> v[i];
- }
- f[0][0] = 0;
- for (int i = 1; i <= m; ++i) {
- for (int j = 0; j <= n; ++j) {
- f[i][j] = f[i - 1][j];
- if (j >= w[i]) {
- f[i][j] = max(f[i][j], f[i - 1][j - w[i]] + v[i]);
- }
- }
- }
- cout << f[m][n] << endl;
- return 0;
- }
07总结
背包在动态规划中是一个非常重要的系列,涉及的类型和变种也非常的多,今天讲的01背包是最基本的一种,不过真正理解了01背包,对后续其它的背包也才能更好的掌握。
本文原创作者:小K,一个思维独特的写手。