Base64
Base64 是什么?是将字节流转换成可打印字符、将可打印字符转换为字节流的一种算法。Base64 使用 64 个可打印字符来表示转换后的数据。
准确的来说,Base64 不算是一种加、解密的算法,它是一种编码、解码的算法。这也是为什么我的用词是编码、解码,而不是加密、解密。
编码原理
这里的讨论的前提是使用 UTF-8 编码
Base64 算法的原理,是将输入流中的字节按每 3 个分为一组,然后每次取 6 个比特,将其转换成表格中对应的数据,一直重复到没有剩余的字符为止,转换表格如下:
编码过程
举个例子,假设我们要对字符串 S.H 进行编码:
- 将其转换成十六进制为 53、2e、48
- 再将十六进制转换成二进制,分别为 01010011、00101110、01001000。这里不足 8 个比特的高位补 0 即可。
- 将其每6个比特分为一组,分别为 010100、110010、111001、001000
- 将其转换成十进制得到,20、50、57、8
- 再根据表格中的转换关系转换可得,U、y、5、I
换句话说,字符串 S.H 通过 Base64 算法编码之后的结果为 Uy5I 。
编码图解
如果觉得文字较难理解,我把上面的流程用图的形式画了出来,可以结合着一起看。
为什么要 每三个 分为一组,因为 3 8 = 24,24 = 4 6,这样子可以刚好可以均分完。
那如果我输入的字节不足三个呢?
例如 SH ?按照上述的做法:
首先将其转换成十六进制53、48,再将其转换成二进制01010011、01001000,再按照每 6 个比特分为一组,就会变成 010100、110100、1000,再转换成十进制得到 20、52、8,最后得到 U0I.
然而这个结果是不正确的,随便去找一个工具输入转换看看都知道,最终结果为 U0g=. 这也说明在输入的字符不足 3 个时,就不是按照之前的方式来处理了。
不足三个字节如何处理?
假设需要编码的字符串还是 SH。
将其转换成二进制为, 01010011、01001000,再按照每 6 个比特分为一组,就会变成010100、110100、1000。
但是可以看到最后一组的比特位不足 6 个,在这种情况下,会进行末尾(低位)补0的操作。补完之后就会变成010100、110100、100000。但是你会发现,这里总共也只有18个比特,不满足 3 个字节一组的原则。在这种情况下,前三组会按照常规的 Base64 进行编码,而缺失的一组则会使用 = 来进行填充。
这样一来,就会变成20、52、32,再根据表格转换可得 U0g ,再加上最后填充的 = ,最终结果就是 U0g=.
以下是图解。
只有一个字节如何处理?
那同理,如果只有一个字符,最后在二进制分组的时候,不足 6 位的低位补 0,分组不满 4 的,直接以 = 号填充。举个例子,假设需要编码的是字符串 S 。
S 的二进制为 01010011 ,按照 6 个比特分为一组,010100、11。第二组明显不满 6 个比特,进行低位补0操作。
低位补0之后结果变成了010100、110000,这里只有 2 组,不满四组,所以这里需要填充 2 个 =。将前面的两组转换成字符,结果为 Uw,再结合填充字符,最终的结果为 Uw==。
关于编码,有人可能会说,你这都是英文,英文转换成十进制再到十六进制很方便,对比 ASCII 码就行,那要是中文呢?实际上,这个跟采取的编码类别有关系。对同样的中文采用不同的编码,最后得到的结果可能都不同。所以我们这里只讨论采用 UTF-8 的场景。
如果是中文,就采用 UTF-8 将中文进行编码,而如果是英文,其转换结果和 ASCII 编码是一样的。
解码原理
因为最终的编码产物中,如果 6 个比特的分组不满 4 组,会有 = 作为填充物,所以一个 base64 完后的产物总是能够被 4 整除。
所以,在解密中,我们每次需要处理 4 个字符,将这 4 个字符编码之后转换成十进制,再转换成二进制,不足 6 位的高位补0,然后将 6 个比特一组的二进制数按原顺序重新分成每 8 个比特一组,也就是一个字节一组。然后将其转换成十六进制,再转换成对应的字符。
解码过程
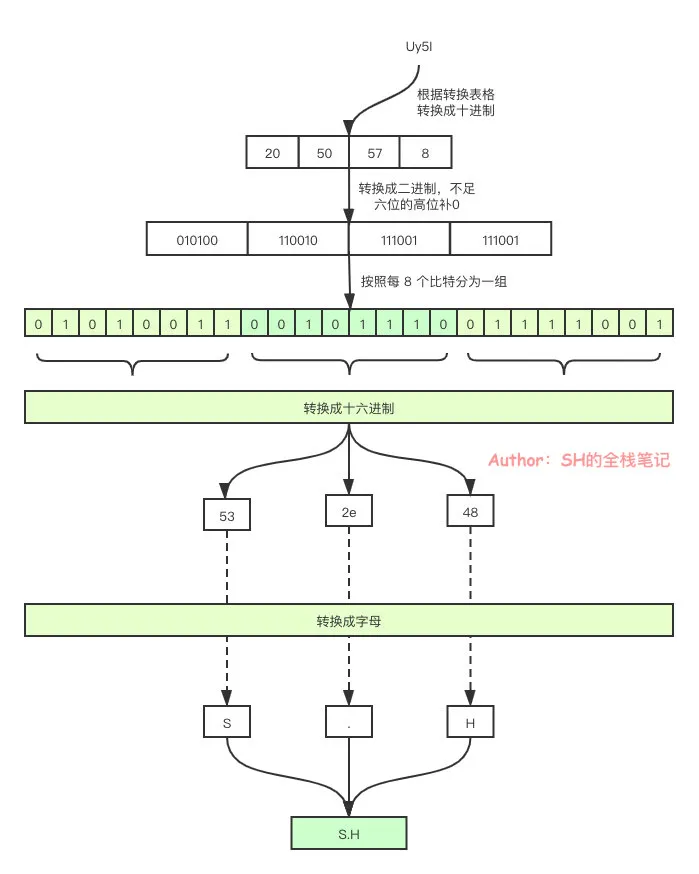
假设我们需要解密的字符为 Uy5I
解密过程就会像:
按照每次处理4个字符的原理,根据表格将其分别转换成十进制20、50、57、8
再将其转换成二进制,不足六位的高位补0,再将其分成每 8 个比特一组
将分组好的比特转换成十六进制,得到53、2e、48
最后将十六进制转换成字母得到S、.、H,也就是 S.H
解码图解
换成图片来说就是如下这样
这里我们处理的是一个比较理想的情况,因为所有的比特位刚好被填充完,那如果带有 = padding 的 base64 是如何进行解密的呢?
这里拿 SH 编码之后的 base64 字符串 U0g= 来做例子
- 首先根据表格,将其转换成十进制20、50、32
- 再将其转换成二进制,不足 6 个比特的高位补0,010100、110100、100000
- 再将其分成每 8 个比特位一组,01010011、01001000、
- 然后再转换成十六进制得53、48
- 转换成字符串可得 SH