本文转载自微信公众号「bigsai」,作者bigsai。转载本文请联系程序员bigsai公众号。
前言
大家好,我是bigsai,今天给大家讲讲Dijkstra算法,下次拿着这个算法找女神少绕路,有女朋友的可以试试行不行的通。
对于Dijkstra算法,很多人可能感觉熟悉而又陌生,可能大部分人比较了解bfs和dfs,而对dijkstra和floyd算法可能知道大概是图论中的某个算法,但是可能不清楚其中的作用和原理,又或许,你曾经感觉它很难,那么,这个时候正适合你重新认识它。
Dijkstra是啥?
其实Dijkstra(迪科斯彻)是一个人,被称为结构程序设计之父,他提出goto有害论、信号量、原语等,创造解决银行家算法、哲学家进餐问题、Dijkstra算法等等,在1972年获得图灵奖(计算机界诺?尔奖),今天咱们就学习Dijkstra算法。
Dijkstra算法干啥的?
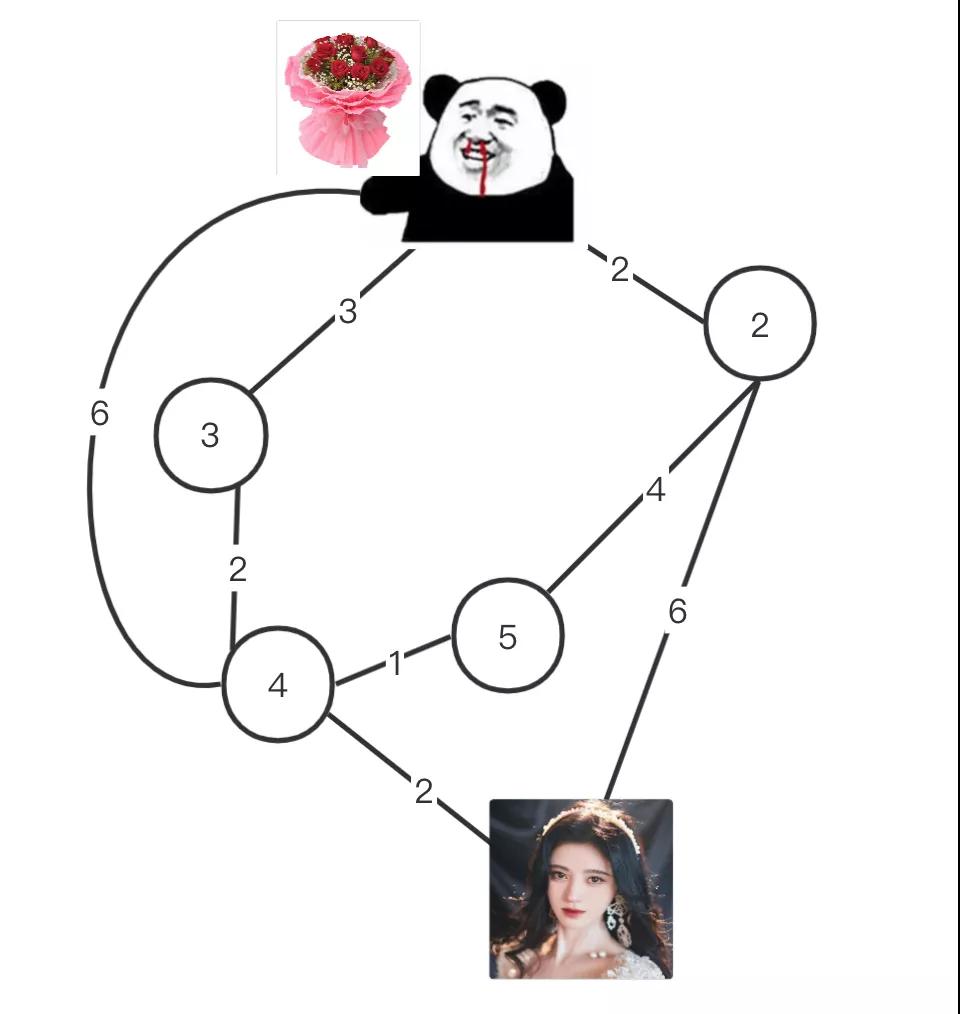
Dijkstra是用来求单源最短路径的,也就是在一个图中,从一个点计算到达其他点的最短距离,再形象一点,就是比如七夕你捧着鲜花去找女神,有点距离,在不堵?没红绿灯情况下怎么找到一条最短的路径:
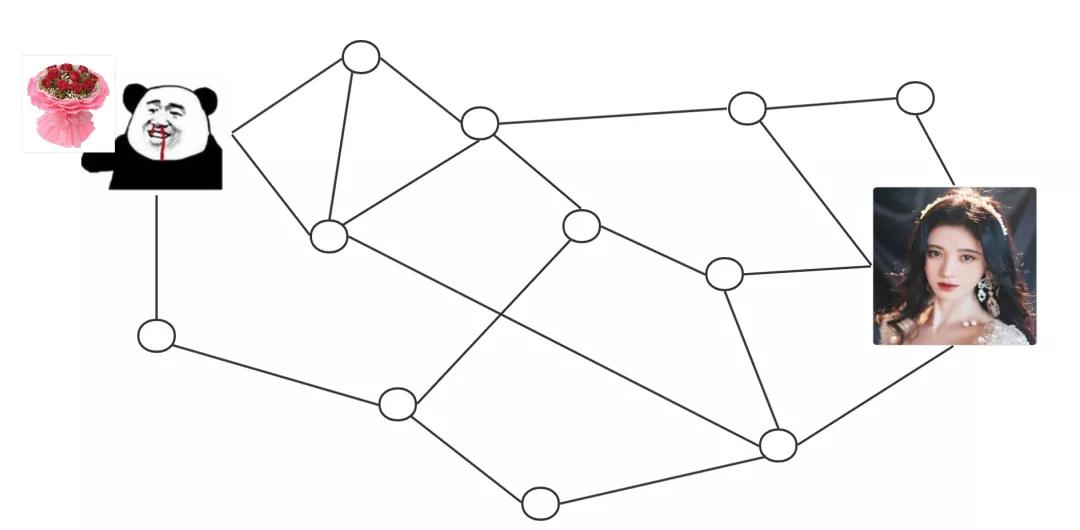
这不是一眼就能看出来嘛!还要什么算法?enum,如果路径很多像这样呢?
就拿上图来说,如果各条路?度都已知,那么可以使用dijkstra算法计算你到图中所有节点的最短距离(不过你想要的就是和女神的距离最近)。不过这个单源最短路径你可能产生一些疑惑:
单源什么意思?
一个源头,从一个顶点出发,Dijkstra算法只能求一个顶点到其他点的最短距离而不能任意两点。
和bfs求的最短路径有什么区别?
bfs求的与其说是路径,不如说是次数。因为bfs他是按照队列一次一次进行加入相邻的点,而两点之间没有权值或者权值相等(代价相同)。bfs求最短路径一般无权值路径(只代表联通性)或者权值相等,仅仅用次数就能表示路径?短的情况,最典型的就是迷宫问题bfs搜索移动一次路径为1就加一次。
Dijkstra在处理具体实例的应用还是很多的,因为具体的问题其实带权更多一些。比如一个城市有多个乡镇,乡镇可能有道路,也可能没有,整个乡镇需要联通,如果想计算每个乡镇到a镇的最短路径,那么Dijkstra就派上了用场。
算法分析
对于一个算法,首先要理解它的运行流程,对于Dijkstra算法而言,首先要知道其适用条件和环境:
一个连通图,若干节点(节点可能有数值),但是路径一定有权值并且不能为负(否则Dijkstra就不适用)。
Dijkstra的核心思想是贪心算法的思想,那什么是贪心呢?
贪心算法(又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所
做出的是在某种意义上的局部最优解。
贪心算法不是对所有问题都能得到整体最优解,关键是贪心策略的选择,选择的贪心策略必须具备无后效性,即某个状态以前的过程不会影响以后的状态,只与当前状态有关。
对于贪心算法,在很多情况都能用到,下面举2个不恰当的例子!
1 .上学时,每周只能带5个苹果,你想带最多,那么选五个苹果你每次都选最大的那个五次下来你就选的最重的那个。
2 .钱币找零,指定币值和相应的数量,用最少的数量凑?某金额。利用贪心策略,优先选择面值大的钱币,直到凑?总金额。
3 .活动选择问题,知道多个活动开始时间、结束时间,想在一个时间内参加最多活动,按照活动结束时间递增排序即可。
上面的策略虽然没有很强的理论数学依据,或者不太好说明,更像一种事实规律经验,并且对于贪心问题具体处理上大部分都需要排序,还可能会遇到规则繁杂的类排序。那么我们的Dijkstra是如何贪心的呢?对于一个点,求图中所有点的最短路径,如果没有正确的方法胡乱想确实很难算出来,并且如果暴力匹配复杂度呈指数级上升不适合解决实际问题。那么我们该怎么想呢?
首先,Dijkstra算法实现上需要这些前提:
- Dijkstra处理的是带正权值的有权图,那么就需要一个二维数组(如果空间大用List数组)存储各个点到点之间边的权值大小 (邻接矩阵或者邻接表存储) ,各个点距离初始化为无穷大。
- 需要一个boolean数组判断哪些点已经确定最短?度路径,那些点没有确定。用一个 int数组记录距离(在算法执行过程有些点最短路径可能被多次更新)。
- 需要优先队列加入已经确定点的周围点。每次抛出从起点最短路径的那个点,直到所有点路径确定最短为止。
简单的概括流程为:
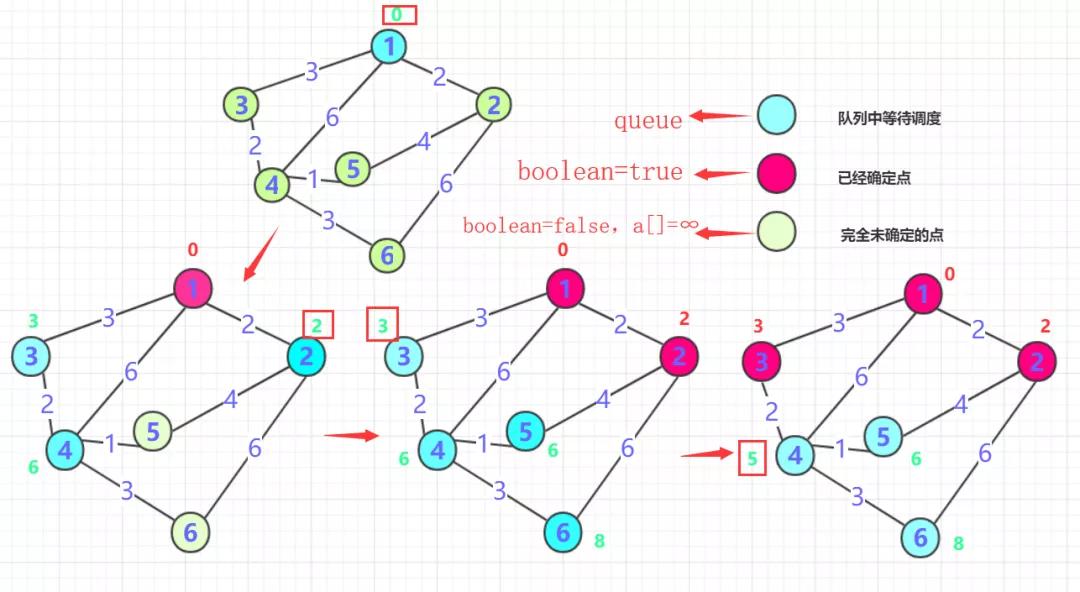
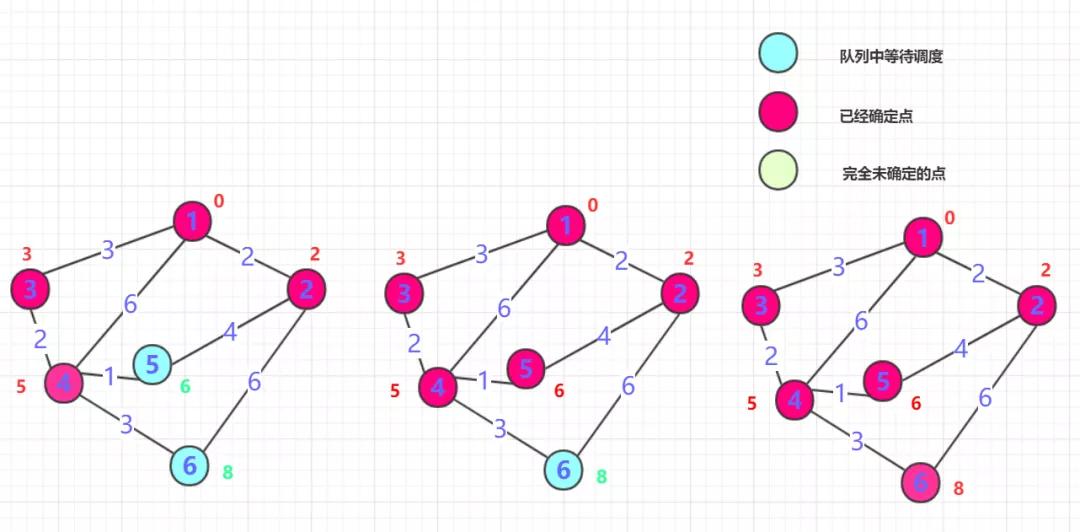
第一步一般从选定点开始抛入优先队列(路径一般为0),boolean数组标记0的位置(最短为0) , 然后0周围连通的点抛入优先队列中(可能是node类),并把各个点的距离记录到对应数组内,此时周围点只是等待调度可能是最短距离,也可能被更新。(如果小于就更新,大于就不动,初始第一次是无穷肯定会更新),第一次就结束了。
从等待调度队列中抛出距离最近的那个点B(第一次就是0周围邻居)。这个点距离一定是最近可以确定的(所有权值都是正的,点的距离只能越来越?,而它的路径是所有可能中的最小的)标记这个点为true表示已经确定,并且将这个点的邻居加入队列(下一次等待调度点为队列中原有的和这个点周围未确定的邻居),并同时判断是否更新B点邻居?度,如果小于则更新!
重复二的操作,直到所有点都确定。
算法实现
代码实现上面有些繁琐,但是也不是很复杂,这里给个Dijkstra算法实现代码:
- package 图论;
- import java.util.ArrayDeque;
- import java.util.Comparator;
- import java.util.PriorityQueue;
- import java.util.Queue;
- import java.util.Scanner;
- public class dijkstra {
- static class node
- {
- int x; //节点编号
- int lenth;//长度
- public node(int x,int lenth) {
- this.x=x;
- this.lenth=lenth;
- }
- }
- public static void main(String[] args) {
- int[][] map = new int[6][6];//记录权值,顺便记录链接情况,可以考虑附加邻接表
- initmap(map);//初始化
- boolean bool[]=new boolean[6];//判断是否已经确定
- int len[]=new int[6];//长度
- for(int i=0;i<6;i++)
- {
- len[i]=Integer.MAX_VALUE;
- }
- Queue<node>q1=new PriorityQueue<node>(com);
- len[0]=0;//从0这个点开始
- q1.add(new node(0, 0));
- int count=0;//计算执行了几次dijkstra
- while (!q1.isEmpty()) {
- node t1=q1.poll();
- int index=t1.x;//节点编号
- int length=t1.lenth;//节点当前点距离
- bool[index]=true;//抛出的点确定
- count++;//其实执行了6次就可以确定就不需要继续执行了 这句可有可无,有了减少计算次数
- for(int i=0;i<map[index].length;i++)
- {
- if(map[index][i]>0&&!bool[i])
- {
- node node=new node(i, length+map[index][i]);
- if(len[i]>node.lenth)//需要更新节点的时候更新节点并加入队列
- {
- len[i]=node.lenth;
- q1.add(node);
- }
- }
- }
- }
- for(int i=0;i<6;i++)
- {
- System.out.println(len[i]);
- }
- }
- static Comparator<node>com=new Comparator<node>() {
- public int compare(node o1, node o2) {
- return o1.lenth-o2.lenth;
- }
- };
- private static void initmap(int[][] map) {
- map[0][1]=2;map[0][2]=3;map[0][3]=6;
- map[1][0]=2;map[1][4]=4;map[1][5]=6;
- map[2][0]=3;map[2][3]=2;
- map[3][0]=6;map[3][2]=2;map[3][4]=1;map[3][5]=3;
- map[4][1]=4;map[4][3]=1;
- map[5][1]=6;map[5][3]=3;
- }
- }
当然,dijkstra算法比较灵活,实现方式也可能有点区别,但是思想是不变的:一个贪心思路。dijkstra执行一次就能够确定一个点,所以只需要执行点的总和次数即可完成整个算法。
一句话概况一下,就是从一个点开始找周围最短的一个,更新相应数据,再找已经确定直接连接的第二个最短点、第三个一直到所有点确定,dijkstra算法就完成了。