本文转载自微信公众号「python与大数据分析」,作者一只小小鸟鸟。转载本文请联系python与大数据分析公众号。
激活函数(Activation Function),就是在人工神经网络的神经元上运行的函数,负责将神经元的输入映射到输出端。
如果不用激活函数,每一层输出都是上层输入的线性函数,无论神经网络有多少层,输出都是输入的线性组合,这种情况就是最原始的感知机。
如果使用的话,激活函数给神经元引入了非线性因素,使得神经网络可以任意逼近任何非线性函数,这样神经网络就可以应用到众多的非线性模型中。
- #!/usr/bin/env python
- # -*- coding: UTF-8 -*-
- # _ooOoo_
- # o8888888o
- # 88" . "88
- # ( | - _ - | )
- # O\ = /O
- # ____/`---'\____
- # .' \\| |// `.
- # / \\|||:|||// \
- # / _|||||-:- |||||- \
- # | | \\\ - /// | |
- # | \_| ''\---/'' | _/ |
- # \ .-\__ `-` ___/-. /
- # ___`. .' /--.--\ `. . __
- # ."" '< `.___\_<|>_/___.' >'"".
- # | | : `- \`.;`\ _ /`;.`/ - ` : | |
- # \ \ `-. \_ __\ /__ _/ .-` / /
- # ==`-.____`-.___\_____/___.-`____.-'==
- # `=---='
- '''
- @Project :pythonalgorithms
- @File :Activationfunction.py
- @Author :不胜人生一场醉@Date :2021/8/11 0:14
- '''
- import numpy as np
- from matplotlib import pyplot as plt
- def drawpic(x, y, label=' ', title=' '):
- plt.figure(figsize=(10, 8))
- ax = plt.gca() # 通过gca:get current axis得到当前轴
- plt.rcParams['font.sans-serif'] = ['SimHei'] # 绘图中文
- plt.rcParams['axes.unicode_minus'] = False # 绘图负号
- plt.plot(x, y, label=label)
- # 设置图片的右边框和上边框为不显示
- ax.spines['right'].set_color('none')
- ax.spines['top'].set_color('none')
- # 挪动x,y轴的位置,也就是图片下边框和左边框的位置
- # data表示通过值来设置x轴的位置,将x轴绑定在y=0的位置
- ax.spines['bottom'].set_position(('data', 0))
- # axes表示以百分比的形式设置轴的位置,即将y轴绑定在x轴50%的位置
- ax.spines['left'].set_position(('axes', 0.5))
- # ax.spines['left'].set_position(('data', 0))
- plt.title(title)
- plt.legend(loc='upper right')
- plt.show()
- if __name__ == '__main__':
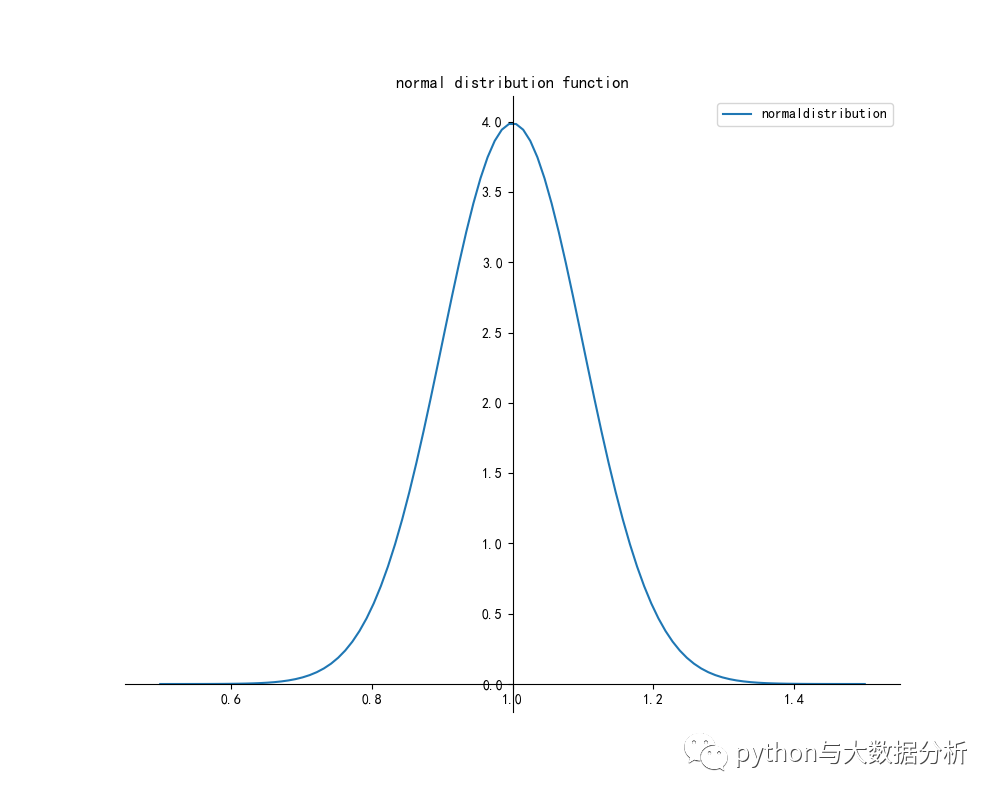
- std = 0.1 # 标准差为0.1
- avg = 1 # 平均值为1
- x = np.linspace(avg - 5 * std, avg + 5 * std, 100)
- y = normaldistribution(x, avg, std)
- drawpic(x, y, 'normaldistribution', 'normal distribution function')
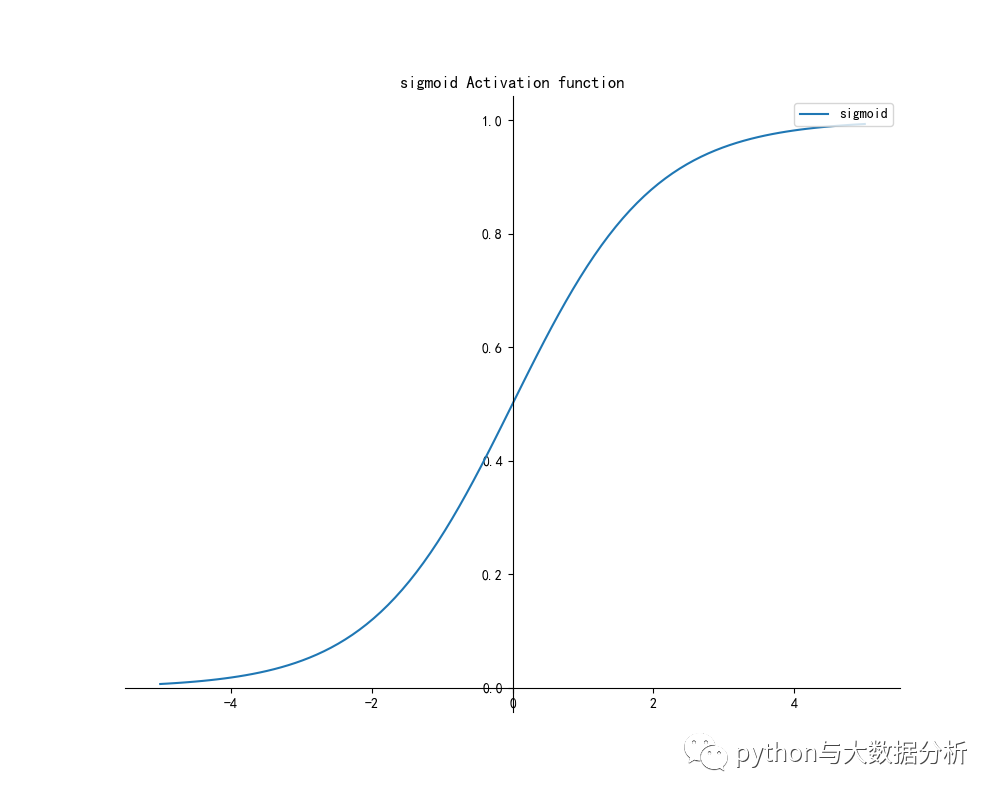
- x = np.linspace(-5, 5, 100)
- y = sigmoid(x)
- drawpic(x, y, 'sigmoid', 'sigmoid Activation function')
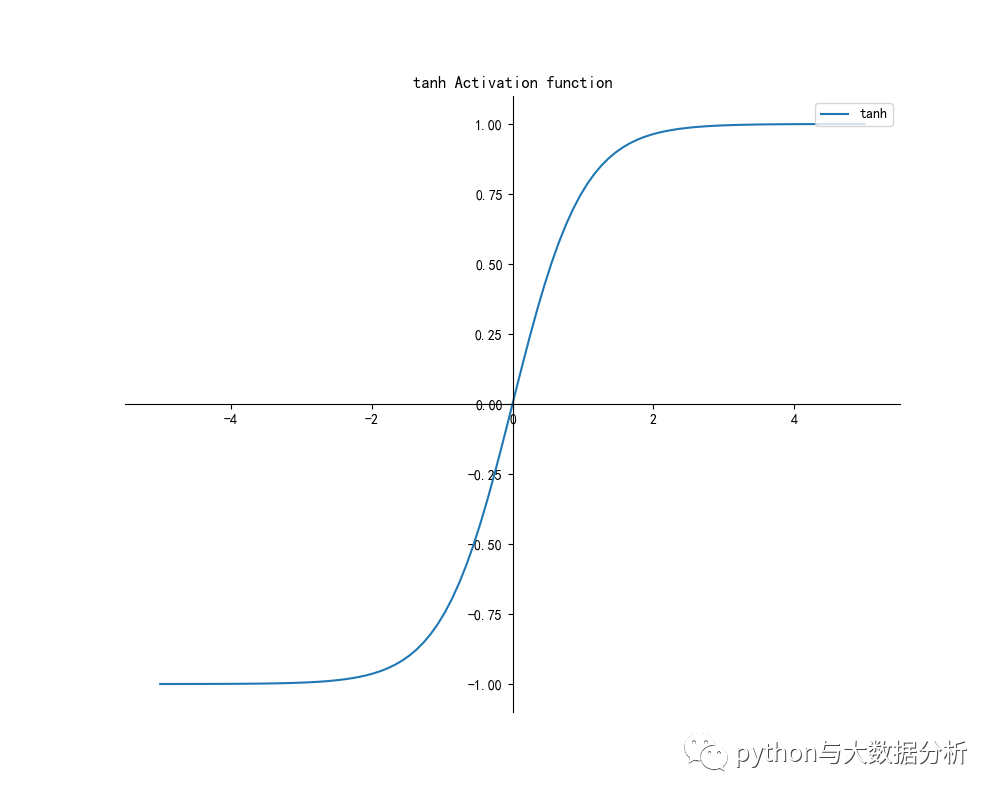
- y = tanh(x)
- drawpic(x, y, 'tanh', 'tanh Activation function')
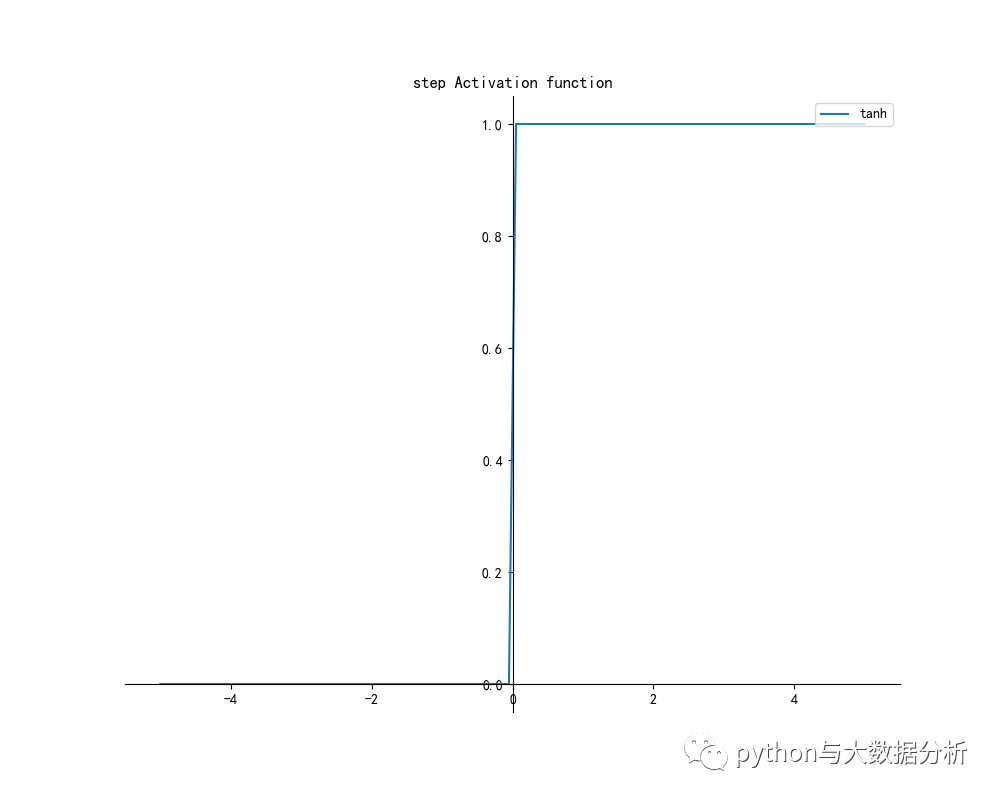
- y = stepfunction(x)
- drawpic(x, y, 'tanh', 'step Activation function')
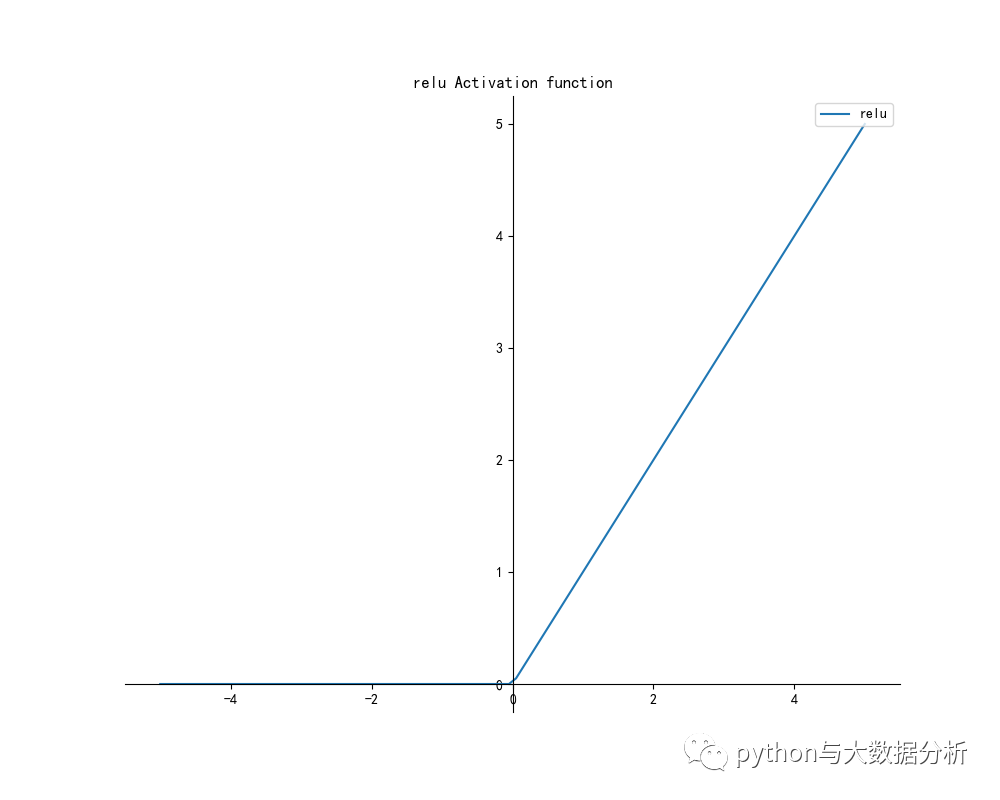
- y = relu(x)
- drawpic(x, y, 'relu', 'relu Activation function')
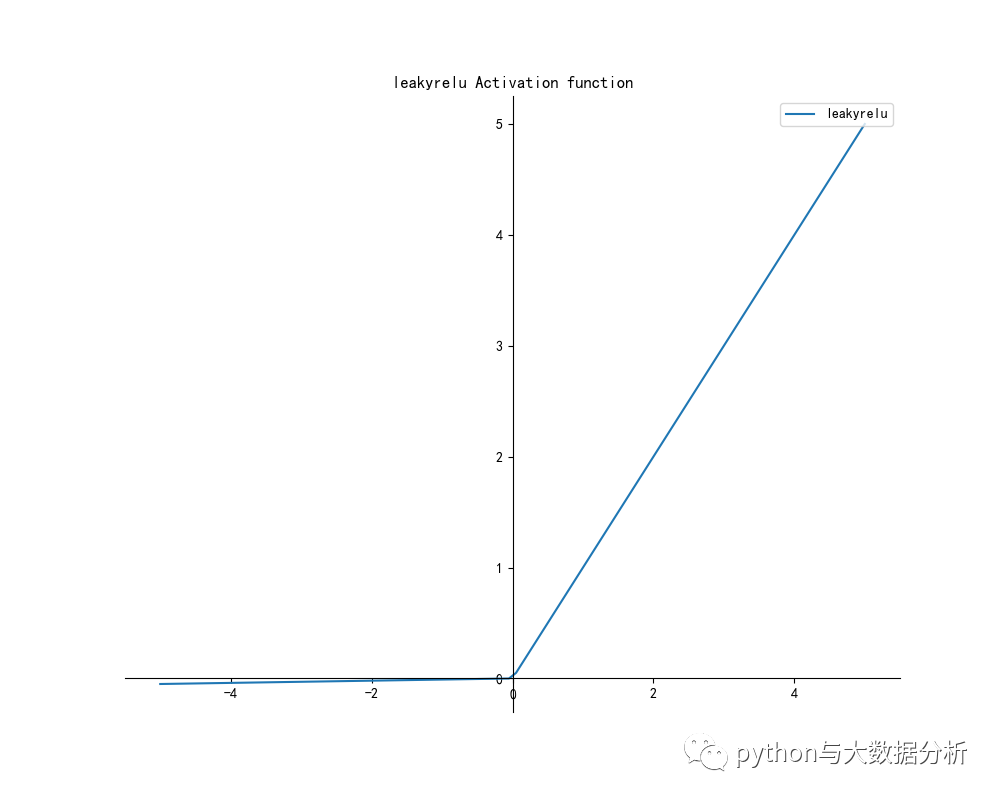
- y = leakyrelu(x)
- drawpic(x, y, 'leakyrelu', 'leakyrelu Activation function')
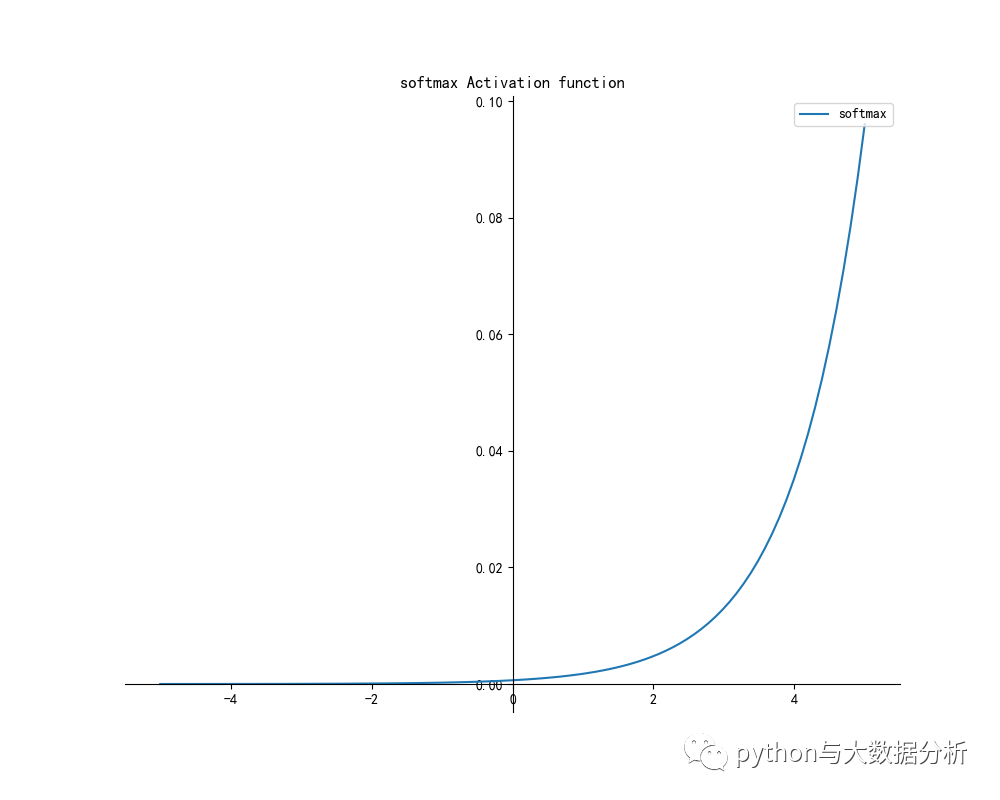
- y = softmax(x)
- drawpic(x, y, 'softmax', 'softmax Activation function')
- # 求正态分布值,avg表示期望值,std表示标准差
- def normaldistribution(x, avg=0, std=1):
- return np.exp(-(x - avg) ** 2 / (2 * std ** 2)) / (np.sqrt(2 * np.pi) * std)
- # return np.exp(-(x - avg) ** 2 / (2 * std ** 2)) / (math.sqrt(2 * math.pi) *
- # Sigmoid函数
- # Sigmoid函数是一个在生物学中常见的S型函数,也称为S型生长曲线。
- # 在信息科学中,由于其单增以及反函数单增等性质,Sigmoid函数常被用作神经网络的阈值函数,将变量映射到0,1之间
- def sigmoid(x):
- return 1 / (1 + np.power(np.e, -x))
- # Tanh函数
- # Tanh是双曲函数中的一个,Tanh()为双曲正切。
- # 在数学中,双曲正切“Tanh”是由基本双曲函数双曲正弦和双曲余弦推导而来。
- # 函数tanh(蓝色)和函数sigmoid(橙色)一样,在其饱和区的接近于0,都容易产生后续梯度消失、计算量大的问题
- def tanh(x):
- return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))
- # 阶跃函数
- def stepfunction(x):
- return np.array(x > 0, dtype=np.int32)
- # ReLU函数
- # Relu激活函数(The Rectified Linear Unit),用于隐层神经元输出。
- # Relu会使一部分神经元的输出为0,这样就造成了网络的稀疏性,并且减少了参数的相互依存关系,缓解了过拟合问题的发生。
- def relu(x):
- return np.maximum(0, x)
- # leaky ReLU函数
- def leakyrelu(x):
- return np.maximum(0.01 * x, x)
- # softmax函数
- # softmax函数可以看做是Sigmoid函数的一般化,用于多分类神经网络输出。
- def softmax(x):
- return np.exp(x) / np.sum(np.exp(x))