本文转载自微信公众号「Piper蛋窝」,作者Piper蛋。转载本文请联系Piper蛋窝公众号。
记录一道题解, 题目来自 Acwing.com 第 11 场周赛.
https://www.acwing.com/activity/content/59/
没参加. 如果让我做的话我做不出来, 难度是困难, 不是一道模板题, 用的知识点 bfs 啥的都简单, 但是考的是分析能力.
我的笔记:
https://github.com/PiperLiu/ACMOI_Journey/tree/master/notes
最大化最短路[1]
给定一个 个点 条边的无向连通图。
图中所有点的编号为 。
图中不含重边和自环。
指定图中的 个点为特殊点。
现在,你必须选择两个特殊点,并在这两个点之间增加一条边。
所选两点之间允许原本就存在边。
我们希望,在增边操作完成以后,点 到点 的最短距离尽可能大。
输出这个最短距离的最大可能值。
注意,图中所有边(包括新增边)的边长均为 。
输入格式
第一行包含三个整数 。
第二行包含 个整数 ,表示 个特殊点的编号, 之间两两不同。
接下来 行,每行包含两个整数 ,表示点 和点 之间存在一条边。
输出格式
一个整数,表示最短距离的最大可能值。
数据范围
前六个测试点满足 。
所有测试点满足 ,,,,。
输入样例1:
- 5 5 3
- 1 3 5
- 1 2
- 2 3
- 3 4
- 3 5
- 2 4
输出样例1:
- 3
输入样例2:
- 5 4 2
- 2 4
- 1 2
- 2 3
- 3 4
- 4 5
输出样例2:
- 3
竞赛中等难度题目,重点在分析。
分析第一步,分情况讨论。
题目中要求,必须在特殊点中选择两个点,这两个点之间会新增一条边。优化目标是,新增边后, 1 到 n 的最短路径最大。
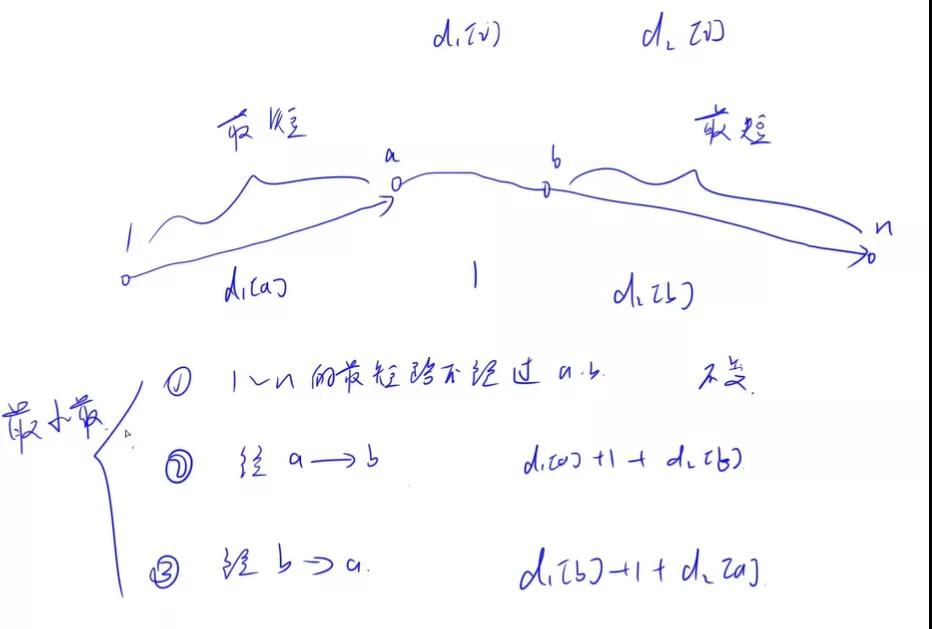
从 1 到 n 的最短路径只可能有以下三种情况(如上图):
- 不经过 a to b 这条线
- 经过 a -> b ,则距离是 x[a] + 1 + y[b]
- 经过 b -> a ,则距离是 x[b] + 1 + y[a]
- 说明:x[a] 为 1 到 a 的距离,y[b] 为 n 到 b 的距离
如果我们在 a 与 b 中增加一条边,则最终最短路的距离为以下三者中取最小值:
- 原有最短路长度
- x[a] + 1 + y[b]
- x[b] + 1 + y[a]
我们没办法改变「原有最短路长度」,因此只能希望 min(x[a] + 1 + y[b], x[b] + 1 + y[a]) 这个值越大越好。
因此,我们要考虑所有特殊点的两两组合,然后,找出最大的 min(x[a] + 1 + y[b], x[b] + 1 + y[a]) 的 a b 组合。
找两两组合
我们没法直接找 min(x[a] + 1 + y[b], x[b] + 1 + y[a]) 的最大值,得进行一步推导:
- x[a] + 1 + y[b] <= x[b] + 1 + y[a]
- 即 x[a] - y[a] <= x[b] - y[b]
- 即,当 x[a] - y[a] <= x[b] - y[b] 时, min(x[a] + 1 + y[b], x[b] + 1 + y[a]) 为 x[a] + 1 + y[b]
- 即,我们找 a, b 满足 x[a] - y[a] <= x[b] - y[b] (这个约束条件也可使我们遍历所有的 a, b 组合),使得 x[a] + 1 + y[b] 最大
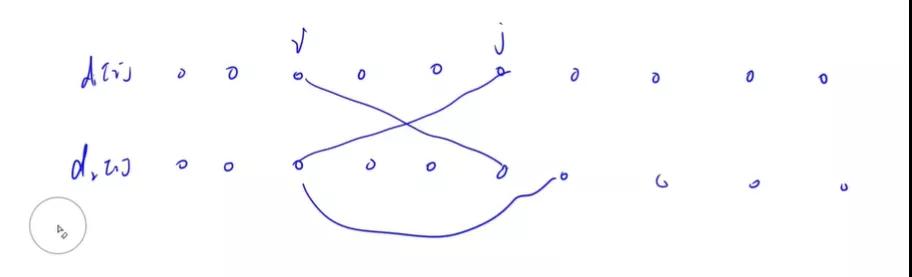
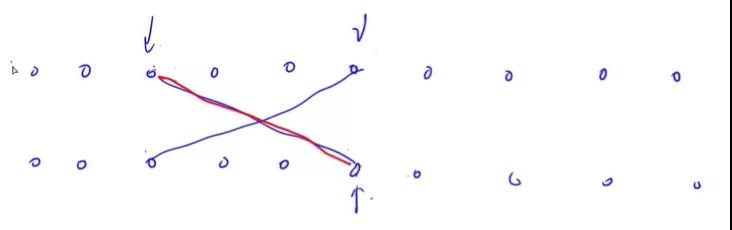
找两两组合
如上,我们将特殊的点按照 x[i] - y[i] 升序排序;我们令 b 为第一层循环:即首先确定 b 的位置(图中为 i ) , a 的话,选择选择从起点到 i 的最大值即可,因为我们的目标是图中红色的线值最大,即 y[b] + 1 + x[a] 。
- #include <iostream>
- #include <cstring>
- #include <algorithm>
- using namespace std;
- const int N = 2e5 + 10, M = 4e5 + 10;
- int n, m, k;
- int a[N], dist1[N], dist2[N]; // 特殊点,题解中的x[]和y[]
- int h[N], e[M], ne[M], idx;
- int q[N]; // bfs 用的队列
- void add(int a, int b)
- {
- e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
- }
- void bfs(int st, int dist[])
- {
- int tt = 0, hh = 0;
- q[0] = st;
- // 传入参数的 dist 是一个指针
- // 不可以用 sizeof dist
- memset(dist, 0x3f, 4 * N);
- dist[st] = 0;
- while (hh <= tt)
- {
- int t = q[hh ++];
- // printf("t = %d h[t] = %d \n", t, h[t]);
- for (int i = h[t]; ~i; i = ne[i])
- {
- int j = e[i];
- if (dist[j] > dist[t] + 1)
- {
- dist[j] = dist[t] + 1;
- // printf("dist[%d] = %d t = %d\n", j, dist[j], tt);
- q[++ tt] = j;
- }
- }
- }
- }
- int main()
- {
- scanf("%d%d%d", &n, &m, &k);
- memset(h, -1, sizeof h); // 莫忘!
- for (int i = 0; i < k; ++ i)
- {
- scanf("%d", &a[i]);
- }
- for (int i = 0; i < m; ++ i)
- {
- int x, y;
- scanf("%d%d", &x, &y);
- add(x, y);
- add(y, x);
- }
- bfs(1, dist1);
- // printf("==bfs2\n");
- bfs(n, dist2);
- // 开始按照题解来,先按照 dist1[i] - dist2[i] 排序
- sort(a, a + k, [&](int a, int b "&") {
- return dist1[a] - dist2[a] < dist1[b] - dist2[b];
- });
- // b 作为最外层循环,找最大的 dist1[a] + 1 + dist2[b]
- int x = dist1[a[0]], res = 0; // 对于第 b = 第一个点,a 也只能为第 0 个点(这里 x 是题解中红线的左上端点)
- for (int i = 1; i < k; i ++ )
- {
- int t = a[i]; // 这里 dist2[t] 是题解中红线的右下端点
- res = max(res, dist2[t] + 1 + x);
- x = max(dist1[t], x);
- }
- // 最后与本来的最短路比较
- res = min(res, dist1[n]);
- printf("%d", res);
- }
经验:
这里,我们将数组传入函数 int dist[] ,不能使用 memset(dist, 0x3f, sizeof dist); 因为 dist 仅仅是一个指针,而非数组;我们的 dist 长度为 N ,且为 int 类型,因此 memset(dist, 0x3f, N * 4);
参考资料
[1]最大化最短路: https://www.acwing.com/problem/content/3800/