回溯算法-机器人的运动范围

[[415476]]

本文转载自微信公众号「神奇的程序员K」，作者神奇的程序员K。转载本文请联系神奇的程序员K公众号。

前言

有一个矩阵，机器人可以从坐标(0,0)的格子开始移动，它每次可以向左、右、上、下移动一格，但是不能进入行坐标和列坐标的数位之和大于K的格子，求这个机器人总共能走多少个格子以及它的行动轨迹。

本文就跟大家分享下这个问题的解决方案 ，欢迎各位感兴趣的开发者阅读本文。

实现思路

在上一篇讲解寻找矩阵中的路径文章中，我们学会了使用回溯算法来访问矩阵中的格子，本文要讨论的这个问题在访问格子之前做了一层判断，如果满足条件就能进入，不满足就无法进入。

我们要做的这层判断为：计算出待访问格子的坐标的数位之和，如果其大于K(最大活动范围)则不能访问。

数位之和：即取出数字中每个位置的值，将其相加得出的结果。例如：19的数位之和就是1 + 9 = 10。

判断当前格子是否已访问

首先，我们需要创建一个与原矩阵大小相同的矩阵，用于标识机器人是否已走这个格子。

在js中无法直接创建指定大小的二维数组，创建思路如下：

• 以矩阵的长度为大小创建一个数组
• 遍历创建好的数组，再以矩阵的第0号数组的长度为大小创建数组，赋值给遍历到的每一项。

判断格子是否可进入

在访问格子时，我们需要判断下要访问的格子是否能进入，我们需要计算出行坐标与列坐标的数位之和，然后将其相加，判断相加后的结果是否大于机器人的最大活动范围(K)。

计算数位之和有两种做法：

• 将数字转为字符串，遍历取出每个字符将其转为数字后再相加
• 对数字进行模运算，将其结果相加，再对数字本身进行/10操作，直至数字小于等于0

开始移动机器人

移动机器人时，我们需要7个参数：

• 矩阵的总行数
• 矩阵的总列数
• 即将进入格子的行坐标
• 即将进入格子的列坐标
• 最大活动范围
• 访问标识矩阵
• 路径矩阵

首先，我们需要进行边界条件判断(递归的终止条件)，条件满足代表该格子无法访问，可行走格子为0(直接返回0)：

• 待访问格子的行坐标大于矩阵的总行数
• 待访问格子的行坐标小于0
• 待访问格子的列坐标大于矩阵的总列数
• 待访问格子的列坐标小于0
• 当前格子已经被访问
• 当前格子不能进入

如果上述条件都满足则表示当前格子可以访问，保存当前格子中的值到行动轨迹中，标识当前格子为已访问状态，已行走格子数+1，并递归尝试当前格子的其它四个方向的格子能否进入。

当递归栈清空后，我们也就得到了机器人总共可以进入的格子总数以及它的行动轨迹。

实现代码

接下来，我们将上述思路转换为TypeScript代码。

格子能否进入函数

我们先来看下判断当前格子能否进入的函数实现，如下所示：

  /** 
   * 判断机器人能否进入目标格子 
   * @param row 行坐标 
   * @param col 列坐标 
   * @param target 临界点 
   * @private 
   */ 
  private checkPath(row: number, col: number, target: number): boolean { 
    // 两坐标的数位之和必须小于等于临界点 
    return sumOfDigits(row) + sumOfDigits(col) <= target; 
  } 
 
// 转字符串实现 
export function sumOfDigits(target: number): number { 
  let finalVal = 0; 
  const computeVal = target.toString(); 
  for (let i = 0; i < computeVal.length; i++) { 
    finalVal += Number(computeVal[i]); 
  } 
  return finalVal; 
} 
 
// 数位之和 - 模运算实现 
export function sumOfDigitsForModular(target: number): number { 
  let finalVal = 0; 
  while (target > 0) { 
    finalVal += Math.floor(target % 10); 
    target /= 10; 
  } 
  return finalVal; 
} 

移动机器人函数

移动机器人至指定格子实现代码如下所示：

/** 
 * 开始移动机器人 
 * @param rows 矩阵总行数 
 * @param cols 矩阵总列数 
 * @param row 待进入格子的行坐标 
 * @param col 待进入格子的列坐标 
 * @param threshold 最大活动范围 
 * @param isVisited 访问标识矩阵 
 * @param matrix 路径矩阵 
 * @private 
 */   
rivate startMoving( 
  rows: number, 
  cols: number, 
  row: number, 
  col: number, 
  threshold: number, 
  isVisited: Array<Array<boolean>>, 
  matrix: Array<Array<T>> 
): number { 
  // 边界条件判断 
  if ( 
    row >= rows || 
    row < 0 || 
    col >= cols || 
    col < 0 || 
    isVisited[row][col] || 
    !this.checkPath(row, col, threshold) 
  ) { 
    return 0; 
  } 
  // 记录当前访问的格子内容 
  this.path += `${matrix[row][col]} -> `; 
  // 标识当前格子已被访问 
  isVisited[row][col] = true; 
  // 格子访问数量+1 
  return ( 
    1 + 
    this.startMoving(rows, cols, row + 1, col, threshold, isVisited, matrix) + 
    this.startMoving(rows, cols, row, col + 1, threshold, isVisited, matrix) + 
    this.startMoving(rows, cols, row - 1, col, threshold, isVisited, matrix) + 
    this.startMoving(rows, cols, row, col - 1, threshold, isVisited, matrix) 
  ); 
} 

主函数

最后，我们来看下主函数的实现，如下所示：

/** 
 * 题目： 
 * 地上有一个m行n列的方格。 
 * 一个机器人从坐标（0，0）的格子开始移动， 
 * 它每次可以向左、右、上、下移动一格，但不能进入行坐标和列坐标的数位之和大于k的格子。 
 * 例如，当k为18时，机器人能够进入方格 （35，37），因为3+5+3+7=18。 
 * 但它不能进入方格（35，38），因为3+5+3+8=19. 请问该机器人能够到达多少个格子？ 
 * @param matrix 矩阵 
 * @param threshold 临界点(最大活动范围) 
 */ 
public movingCount(matrix: Array<Array<T>>, threshold = 0): number { 
  if (threshold < 0 || matrix.length <= 0) { 
    return 0; 
  } 
  // 获取方格的总行数与总列数 
  const rows = matrix.length; 
  const cols = matrix[0].length; 
  // 创建标记数组，用于标识格子是否被访问 
  const isVisited: Array<Array<boolean>> = new Array(rows); 
  for (let i = 0; i < isVisited.length; i++) { 
    isVisited[i] = new Array(cols); 
  } 
  // 从0,0位置开始移动，计算总的移动格子数量 
  return this.startMoving(rows, cols, 0, 0, threshold, isVisited, matrix); 
} 

完整代码请移步：Backtracking.ts#L80

编写测试用例

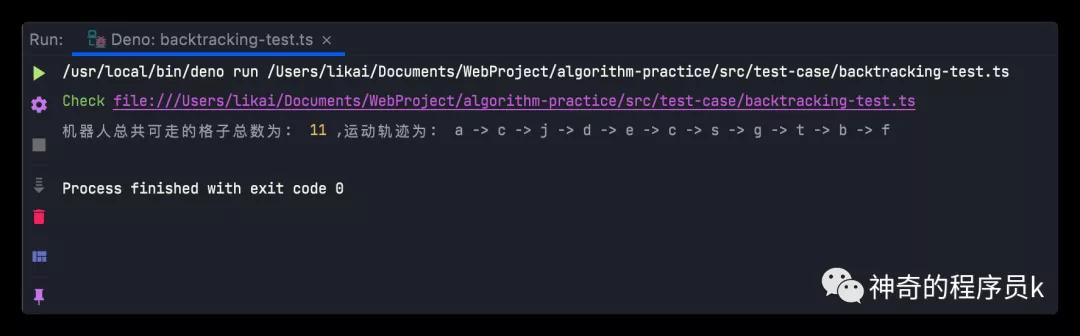
接下来，我们构造一个矩阵来验证下上述代码能否正确执行，如下所示：

const pathArr = [ 
  ["a", "b", "t", "g"], 
  ["c", "f", "c", "s"], 
  ["j", "d", "e", "h"] 
]; 
 
const backtracking = new Backtracking<string>(); 
const totalCount = backtracking.movingCount(pathArr, 4); 
const path = backtracking.path; 
console.log( 
  "机器人总共可走的格子总数为: ", 
  totalCount, 
  ",运动轨迹为: ", 
  path.substr(0, path.length - 3) 
); 

执行结果如下所示：