Nacos之随机权重负载均衡算法

引言

Nacos在Client选择节点时提供了一种基于权重的随机算法，通过源码分析掌握其实现原理，方便实战中加以运用。

一、内容提要

下面以图示的方式贯穿下随机权重负载均衡算法的流程：

节点列表

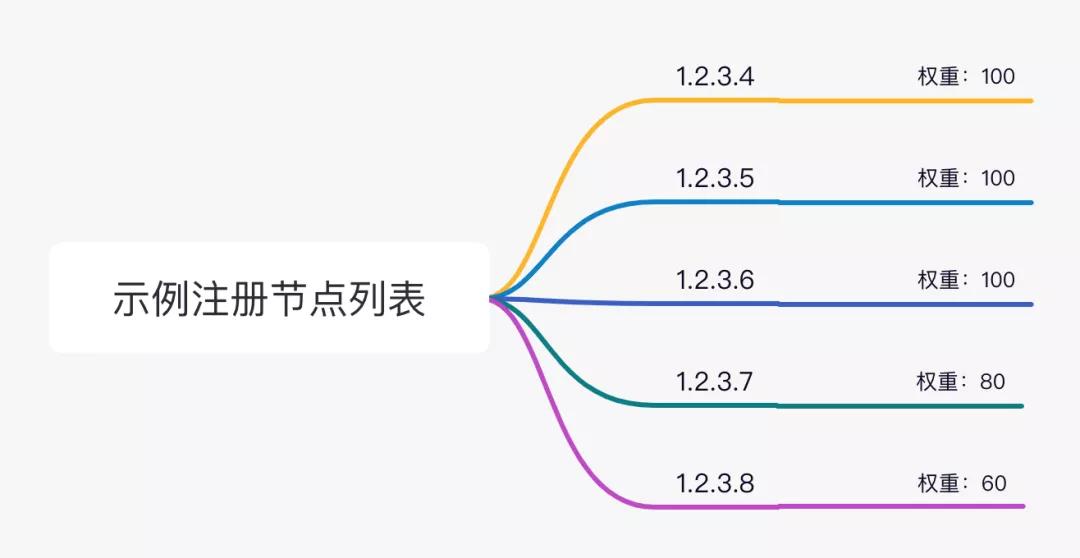
假设注册了5个节点，每个节点的权重如下。

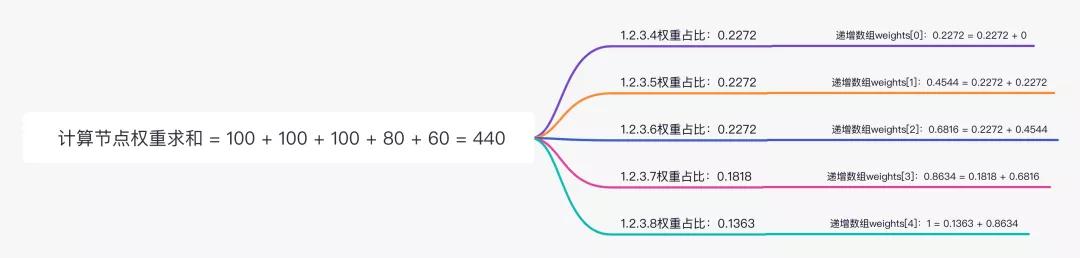
组织递增数组

目的在于形成weights数组，该数组元素取值[0~1]范围，元素逐个递增，计算过程如下图示。另外注意非健康节点或者权重小于等于0的不会被选择。

随机算法

通过生成[0~1]范围的随机数，通过二分法查找递增数组weights[]接近的index，再从注册节点列表中返回节点。

二、源码分析

随机权重负载均衡算法是在NacosNamingService#selectOneHealthyInstance提供，一起走查下。

@Override 
public Instance selectOneHealthyInstance(String serviceName, String groupName, boolean subscribe) 
  throws NacosException { 
  return selectOneHealthyInstance(serviceName, groupName, new ArrayList<String>(), subscribe); 
} 

@Override 
public Instance selectOneHealthyInstance(String serviceName, String groupName, List<String> clusters, 
                                         boolean subscribe) throws NacosException { 
  String clusterString = StringUtils.join(clusters, ","); 
  // 注解@1 
  if (subscribe) { 
    ServiceInfo serviceInfo = serviceInfoHolder.getServiceInfo(serviceName, groupName, clusterString); 
    if (null == serviceInfo) { 
      serviceInfo = clientProxy.subscribe(serviceName, groupName, clusterString); 
    } 
    return Balancer.RandomByWeight.selectHost(serviceInfo); 
  } else { 
    // 注解@2 
    ServiceInfo serviceInfo = clientProxy 
      .queryInstancesOfService(serviceName, groupName, clusterString, 0, false); 
    return Balancer.RandomByWeight.selectHost(serviceInfo); 
  } 
} 

注解@1 已订阅「从缓存获取注册节点列表」，默认subscribe为true。

注解@2 从 「从服务器获取注册节点列表」

protected static Instance getHostByRandomWeight(List<Instance> hosts) { 
  NAMING_LOGGER.debug("entry randomWithWeight"); 
  if (hosts == null || hosts.size() == 0) { 
    NAMING_LOGGER.debug("hosts == null || hosts.size() == 0"); 
    return null; 
  } 
  NAMING_LOGGER.debug("new Chooser"); 
  List<Pair<Instance>> hostsWithWeight = new ArrayList<Pair<Instance>>(); 
  for (Instance host : hosts) { 
    if (host.isHealthy()) {  // 注解@3 
      hostsWithWeight.add(new Pair<Instance>(host, host.getWeight())); 
    } 
  } 
  NAMING_LOGGER.debug("for (Host host : hosts)"); 
  Chooser<String, Instance> vipChooser = new Chooser<String, Instance>("www.taobao.com"); 
  // 注解@4 
  vipChooser.refresh(hostsWithWeight); 
  NAMING_LOGGER.debug("vipChooser.refresh"); 
  // 注解@5 
  return vipChooser.randomWithWeight(); 
} 

注解@3 非健康节点不会被选中，组装Pair的列表，包含健康节点的权重和Host信息

注解@4 刷新需要的数据，具体包括三部分：所有健康节点权重求和、计算每个健康节点权重占比、组织递增数组。

public void refresh() { 
    Double originWeightSum = (double) 0; 
    // 注解@4.1 
    for (Pair<T> item : itemsWithWeight) { 
 
        double weight = item.weight(); 
        // ignore item which weight is zero.see test_randomWithWeight_weight0 in ChooserTest 
        // weight小于等于 0的将会剔除 
        if (weight <= 0) { 
            continue; 
        } 
 
        items.add(item.item()); 
 
        // 值如果无穷大 
        if (Double.isInfinite(weight)) { 
            weight = 10000.0D; 
        } 
 
        // 值如果为非数字值 
        if (Double.isNaN(weight)) { 
            weight = 1.0D; 
        } 
 
        // 累加权重总和 
        originWeightSum += weight; 
    } 
 
    // 注解@4.2 
    double[] exactWeights = new double[items.size()]; 
    int index = 0; 
    for (Pair<T> item : itemsWithWeight) { 
        double singleWeight = item.weight(); 
        //ignore item which weight is zero.see test_randomWithWeight_weight0 in ChooserTest 
        if (singleWeight <= 0) { 
            continue; 
        } 
        // 每个节点权重的占比 
        exactWeights[index++] = singleWeight / originWeightSum; 
    } 
 
    // 注解@4.3 
    weights = new double[items.size()]; 
    double randomRange = 0D; 
    for (int i = 0; i < index; i++) { 
        weights[i] = randomRange + exactWeights[i]; 
        randomRange += exactWeights[i]; 
    } 
   
    double doublePrecisionDelta = 0.0001; 
 
    if (index == 0 || (Math.abs(weights[index - 1] - 1) < doublePrecisionDelta)) { 
        return; 
    } 
    throw new IllegalStateException( 
            "Cumulative Weight caculate wrong , the sum of probabilities does not equals 1."); 
} 

注解@4.1 所有健康节点权重求和originWeightSum

注解@4.2 计算每个健康节点权重占比exactWeights数组

注解@4.3 组织递增数组weights，每个元素值为数组前面元素之和

以一个例子来表示这个过程，假设有5个节点：

1.2.3.4 100 
1.2.3.5 100 
1.2.3.6 100 
1.2.3.7 80 
1.2.3.8 60 

步骤一 计算节点权重求和

• originWeightSum = 100 + 100 + 100 + 80 + 60 = 440

步骤二 计算每个节点权重占比

• exactWeights[0] = 0.2272
• exactWeights[1] = 0.2272
• exactWeights[2] = 0.2272
• exactWeights[3] = 0.1818
• exactWeights[4] = 0.1363

步骤三 组织递增数组weights

• weights[0] = 0.2272
• weights[1] = 0.4544
• weights[2] = 0.6816
• weights[3] = 0.8634
• weights[4] = 1

注解@5 随机选取一个，逻辑如下：

public T randomWithWeight() { 
    Ref<T> ref = this.ref; 
    // 注解@5.1 
    double random = ThreadLocalRandom.current().nextDouble(0, 1); 
    // 注解@5.2 
    int index = Arrays.binarySearch(ref.weights, random); 
    // 注解@5.3 
    if (index < 0) { 
        index = -index - 1; 
    } else { 
        // 注解@5.4 
        return ref.items.get(index); 
    } 
 
    // 返回选中的元素 
    if (index >= 0 && index < ref.weights.length) { 
        if (random < ref.weights[index]) { 
            return ref.items.get(index); 
        } 
    } 
 
    /* This should never happen, but it ensures we will return a correct 
     * object in case there is some floating point inequality problem 
     * wrt the cumulative probabilities. */ 
    return ref.items.get(ref.items.size() - 1); 
} 

注解@5.1 产生0到1区间的随机数

注解@5.2 二分法查找数组中接近的值

注解@5.3 没有命中返回插入数组理想索引值

注解@5.4 命中直接返回选中节点

小结： 一种基于权重的随机算法的实现过程，扒开看也不复杂。

本文转载自微信公众号「瓜农老梁」，可以通过以下二维码关注。转载本文请联系瓜农老梁公众号。