Python实现之一阶二阶导数-python求一阶导数

[[415180]]

本文转载自微信公众号「python与大数据分析」，作者一只小小鸟鸟。转载本文请联系python与大数据分析公众号。

函数的和、差、积、商的求导法则

u=u(x),v=v(x)

(u+v)'=u'+v'

(u-v)'=u'-v'

(Cu)'=Cu'

(uv)'=u'v+uv'

(u/v)'=(u'v-uv')/v^2

复合函数求导法则

y=f(u)，u=φ(v)

复合函数y=f[φ(v)]的导数为

dy/dx=dy/du*du/dx=f'(u)*φ'(v)

(u-v+z)'=u'-v'+z'，且(Cu)'=Cu'

exam1:

y =2*x*^3 -5*x^2+3*x-7

y'=6*x^2-10x+3+0

exam2:

f(x)=x^3+4cosx-sin(π/2)

f'(x)=(x^3)‘+(4cosx)‘-(sin(π/2))‘=3x^2-4sinx-0

f'(π/2)=f'(x)|x=(π/2)=3x^2-4sinx=3*(π/2)^2-4sin(π/2)=3/4π^2-4

exam3:

y=√x*lnx

y'=(√x)'*lnx+√x*(lnx)'=1/(2*√x)*lnx+√x*1/x=1/(√x)*(1/2*lnx+1)

exam4:

y=e^x(sinx+cosx)

y'=(e^x)'(sinx+cosx)+e^x(sinx+cosx)'=e^x(sinx+cosx)+e^x(cosx-sinx)=2e^xcosx

高阶导数

y=f(x)

y'=f'(x)

y''=(y')'=d^2y/dx^2=d/dx(dy/dx)

导数的应用：函数单调性

通过函数的导数的值，可以判断出函数的单调性、驻点以及极值点：

若导数大于0，则单调递增;

若导数小于0，则单调递减;

导数等于零d的点为函数驻点

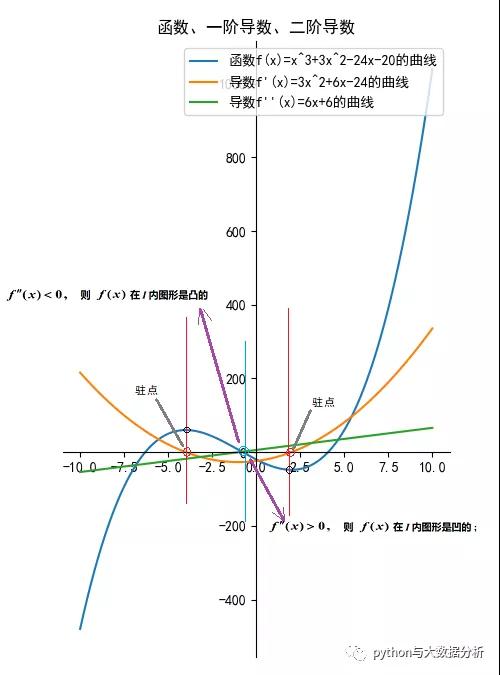
曲线的凹凸性，设函数f(x) 在区间I 上有二阶导数

(1) 在 I 内 f''(x)>0则 f(x)在 I 内图形是凹的 ;

(2) 在 I 内 f''(x)<0则 f(x)在 I 内图形是凸的 .

#!/usr/bin/env python 
# -*- coding: UTF-8 -*- 
#                     _ooOoo_ 
#                   o8888888o 
#                    88" . "88 
#                 ( | -  _  - | ) 
#                     O\ = /O 
#                 ____/`---'\____ 
#                  .' \\| |// `. 
#                 / \\|||:|||// \ 
#               / _|||||-:- |||||- \ 
#                | | \\\ - /// | | 
#              | \_| ''\---/'' | _/ | 
#               \ .-\__ `-` ___/-. / 
#            ___`. .' /--.--\ `. . __ 
#         ."" '< `.___\_<|>_/___.' >'"". 
#       | | : `- \`.;`\  _ /`;.`/ - ` : | | 
#          \ \ `-. \_ __\ /__ _/ .-` / / 
#      ==`-.____`-.___\_____/___.-`____.-'== 
#                     `=---=' 
''' 
@Project ：pythonalgorithms  
@File ：Nderivatives.py 
@Author ：不胜人生一场醉@Date ：2021/8/3 1:17  
''' 
import matplotlib.pyplot as plt 
import numpy as np 
import math 
import sympy 
 
if __name__ == '__main__': 
    nderivativeplot() 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.

# f(x)=x^3+3x^2-24x-20 
# f'(x)=3x^2+6x-24 
# f''(x)=6x+6 
def nderivativeplot(): 
    plt.figure(figsize=(5, 8)) 
    ax = plt.gca()  # 通过gca:get current axis得到当前轴 
    plt.rcParams['font.sans-serif'] = ['SimHei']  # 绘图中文 
    plt.rcParams['axes.unicode_minus'] = False  # 绘图负号 
    x = np.linspace(-10,10, 200) 
    y = np.power(x,3)+3*np.power(x,2)-24*x-20 
    yd = 3*np.power(x,2)+6*x-24 
    ydd=6*x+6 
    label = '函数f(x)=x^3+3x^2-24x-20的曲线' 
    plt.plot(x, y, label=label) 
    label = "导数f'(x)=3x^2+6x-24的曲线" 
    plt.plot(x, yd, label=label) 
    label = "导数f''(x)=6x+6的曲线" 
    plt.plot(x, ydd, label=label) 
 
 
    # 设置图片的右边框和上边框为不显示 
    ax.spines['right'].set_color('none') 
    ax.spines['top'].set_color('none') 
 
    # 挪动x，y轴的位置，也就是图片下边框和左边框的位置 
    # data表示通过值来设置x轴的位置，将x轴绑定在y=0的位置 
    ax.spines['bottom'].set_position(('data', 0)) 
    # axes表示以百分比的形式设置轴的位置，即将y轴绑定在x轴50%的位置 
    # ax.spines['left'].set_position(('axes', 0.5)) 
    ax.spines['left'].set_position(('data', 0)) 
    plt.title("函数、一阶导数、二阶导数") 
    plt.legend(loc='upper right') 
    plt.show() 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.