本文转载自微信公众号「Piper蛋窝」,作者Piper蛋 。转载本文请联系Piper蛋窝公众号。
上上周 力扣双周赛 T4[1] 和 Acwing 第 9 场周赛最后一题[2] 的考点竟然都是单调栈。
对单调栈理解不透彻,当时没想到。
其实单调栈题目的特征很明显。
一般来讲,单调栈题目需要就数学关系进行分析,比如:
- 我们需要寻找一个非凹子序列
- 即我们需要寻找两个子序列,一个在左边单调增,一个在右边单调减,因此用两个单调栈分别从左往右和从右往左预处理序列
非凹的序列应该只有这三种
单调栈有什么特性呢?我该怎么想到:「喔,这个问题可以用单调栈来解决呢?」我总结了一下:
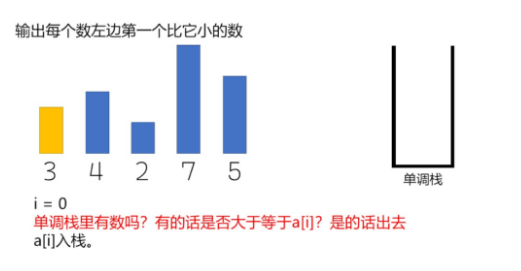
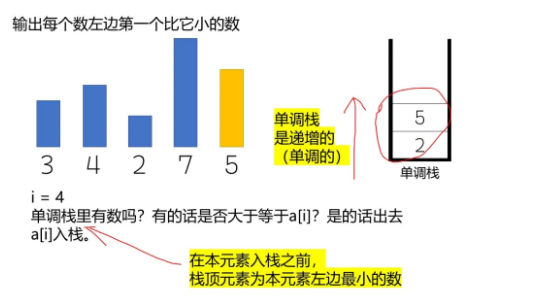
遍历到 i 时,总会把 i 推入栈,总会保证栈顶到栈底是降序的。因此在把 i 入栈前,从栈顶开始,把比 i 高(大于等于)的都 pop 出来。
即,单调栈是一种预处理技术。用 的时间处理一个长度为 的序列,会得到这 个元素的最相邻的比自己小的元素 / 比自己大的元素 / 以该元素结尾的递增或递减子序列长度等。
这非常 amazing ,按理说,想要得到 个信息,起码要用 或者 的时间吧。
搞个动图和经典例题解释一下。
我们有一个长度为 5 的序列:3 4 2 7 5 ,我们希望找到每一个数左边的第一个比自己小的数。我们知道分别是:没有 3 没有 2 2 。如何设计一个算法让计算机自动找到这些数呢?见下面的动图。
因此咱们可以总结出其性质如下。
例题:寻找左边最近的比自己小的数
来源:AcWing在线题库[3]
- 给定一个长度为 N 的整数数列,输出每个数左边第一个比它小的数,如果不存在则输出 ?1。
输入格式
- 第一行包含整数 N,表示数列长度。
- 第二行包含 N 个整数,表示整数数列。
输出格式
- 共一行,包含 N 个整数,其中第 i 个数表示第 i 个数的左边第一个比它小的数,如果不存在则输出 ?1。
分析:
- 首先想到两层循环,暴力做法;接下来想哪里可以优化(类似双指针的思路)
- 注意一个性质,如果 i < j ,且 a[i] >= a[j] ,那么我们之后都没必要管 i 了,因为 j 比 i 更加靠右,且值更小;后面的数向左搜索的过程中,碰到 j 觉得不行(还没 a[j] 大呢),碰到 i 更不会觉得行了(更不会有 a[i] 大)
- 用单调栈实现
- #include <iostream>
- using namespace std;
- const int N = 1e5 + 10;
- int stk[N], tt;
- int main()
- {
- int n, x;
- cin >> n;
- for (int i = 0; i < n; i ++)
- {
- cin >> x;
- while (tt && stk[tt] >= x) tt --;
- if (tt) cout << stk[tt] << " ";
- else cout << -1 << " ";
- stk[++ tt] = x;
- }
- return 0;
- }
参考资料
[1]力扣双周赛 T4: https://leetcode-cn.com/problems/number-of-visible-people-in-a-queue/
[2]Acwing 第 9 场周赛最后一题: https://www.acwing.com/problem/content/3783/
[3]AcWing在线题库: https://www.acwing.com/problem/content/832/