Python实现之初等函数三之三角函数-python 三角函数

本文转载自微信公众号「python与大数据分析」，作者一只小小鸟鸟。转载本文请联系python与大数据分析公众号。

三角函数在python和numpy中实现的不够全面，主要包括cos, cosh, sin sinh, tan, tanh三角函数和arccos, arccosh, arcsin, arcsinh, arctan, arctanh反三角函数，cot,sec,csc,arccot,arcsec,arccsc均为提供，不过可以通过其他函数进行组合或变形得以实现。

三角函数是基本初等函数之一，是以角度(数学上最常用弧度制，下同)为自变量，角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。也可以等价地用与单位圆有关的各种线段的长度来定义。三角函数在研究三角形和圆等几何形状的性质时有重要作用，也是研究周期性现象的基础数学工具。在数学分析中，三角函数也被定义为无穷级数或特定微分方程的解，允许它们的取值扩展到任意实数值，甚至是复数值。

反三角函数是一种基本初等函数。它是反正弦arcsin x，反余弦arccos x，反正切arctan x，反余切arccot x，反正割arcsec x，反余割arccsc x这些函数的统称，各自表示其正弦、余弦、正切、余切，正割，余割为x的角

#!/usr/bin/env python 
# -*- coding: UTF-8 -*- 
#                     _ooOoo_ 
#                   o8888888o 
#                    88" . "88 
#                 ( | -  _  - | ) 
#                     O\ = /O 
#                 ____/`---'\____ 
#                  .' \\| |// `. 
#                 / \\|||:|||// \ 
#               / _|||||-:- |||||- \ 
#                | | \\\ - /// | | 
#              | \_| ''\---/'' | _/ | 
#               \ .-\__ `-` ___/-. / 
#            ___`. .' /--.--\ `. . __ 
#         ."" '< `.___\_<|>_/___.' >'"". 
#       | | : `- \`.;`\  _ /`;.`/ - ` : | | 
#          \ \ `-. \_ __\ /__ _/ .-` / / 
#      ==`-.____`-.___\_____/___.-`____.-'== 
#                     `=---=' 
''' 
@Project ：pythonalgorithms  
@File ：trigonometric.py 
@Author ：不胜人生一场醉@Date ：2021/7/26 23:28  
''' 
import matplotlib.pyplot as plt 
import numpy as np 
import math 
import mpl_toolkits.axisartist as axisartist  # 导入坐标轴加工模块 
# 三角函数是基本初等函数之一，是以角度（数学上最常用弧度制，下同）为自变量，角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。 
# 也可以等价地用与单位圆有关的各种线段的长度来定义。三角函数在研究三角形和圆等几何形状的性质时有重要作用， 
# 也是研究周期性现象的基础数学工具。 
# 在数学分析中，三角函数也被定义为无穷级数或特定微分方程的解，允许它们的取值扩展到任意实数值，甚至是复数值。 
# 正弦函数 ：y =sin x 
# 正弦（sine），数学术语，在直角三角形中，任意一锐角∠A的对边与斜边的比叫做∠A的正弦，记作sinA（由英语sine一词简写得来），即sinA=∠A的对边/斜边。 
# 余弦函数 ：y =cos x 
# 余弦（余弦函数）。在Rt△ABC（直角三角形）中，∠C=90°（如概述图所示），∠A的余弦是它的邻边比三角形的斜边，即cosA=b/c，也可写为cosa=AC/AB。余弦函数：f(x)=cosx（x∈R） 
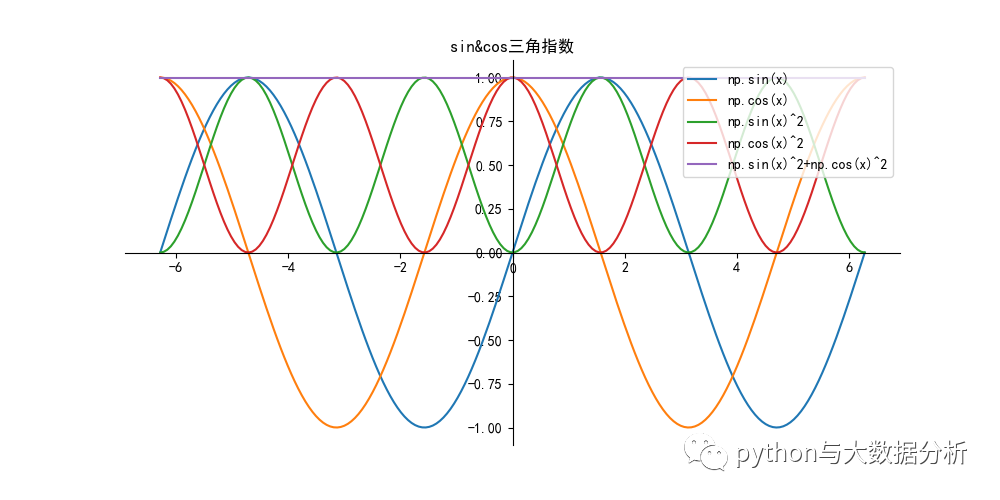
# 平方和关系 
# （sinα）^2 +（cosα）^2=1 
# 积的关系 
# sinα = tanα × cosα（即sinα / cosα = tanα ） 
# cosα = cotα × sinα （即cosα / sinα = cotα） 
# tanα = sinα × secα (即 tanα / sinα = secα) 
# 倒数关系 
# tanα × cotα = 1 
# sinα × cscα = 1 
# cosα × secα = 1 
# 商的关系 
# sinα / cosα = tanα = secα / cscα 
# 和角公式 
# sin ( α ± β ) = sinα · cosβ ± cosα · sinβ 
# sin ( α + β + γ ) = sinα · cosβ · cosγ + cosα · sinβ · cosγ + cosα · cosβ · sinγ - sinα · sinβ · sinγ 
# cos ( α ± β ) = cosα cosβ ∓ sinβ sinα 
# tan ( α ± β ) = ( tanα ± tanβ ) / ( 1 ∓ tanα tanβ ) 
# 倍角半角公式 
# sin ( 2α ) = 2sinα · cosα [1] 
# sin ( 3α ) = 3sinα - 4sin & sup3 ; ( α ) = 4sinα · sin ( 60 + α ) sin ( 60 - α ) 
# sin ( α / 2 ) = ± √( ( 1 - cosα ) / 2) 
# 级数展开 
# sin x = x - x3 / 3! + x5 / 5! - ... ( - 1 ) k - 1 * x 2 k - 1 / ( 2k - 1 ) ! + ... ( - ∞ < x < ∞ ) 
# 导数 
# （ sinx ） ' = cosx 
# （ cosx ) ' = ﹣ sinx 
 
if __name__ == "__main__": 
   sincosfunction() 
   tanctnfunction() 
   seccscfunction() 
   arcsincosfunction() 
   arccscfunction() 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.

def sincosfunction(): 
   plt.figure(figsize=(10, 5)) 
   ax = plt.gca()  # 通过gca:get current axis得到当前轴 
   plt.rcParams['font.sans-serif'] = ['SimHei']  # 绘图中文 
   plt.rcParams['axes.unicode_minus'] = False  # 绘图负号 
   x = np.linspace(-np.pi*2, np.pi*2, 200) 
 
   y = np.sin(x) 
   label = 'np.sin(x)' 
   plt.plot(x, y, label=label) 
   y = np.cos(x) 
   label = 'np.cos(x)' 
   plt.plot(x, y, label=label) 
   y = np.power(np.sin(x),2) 
   label = 'np.sin(x)^2' 
   plt.plot(x, y, label=label) 
   y = np.power(np.cos(x),2) 
   label = 'np.cos(x)^2' 
   plt.plot(x, y, label=label) 
   y = np.power(np.cos(x), 2)+np.power(np.sin(x),2) 
   label = 'np.sin(x)^2+np.cos(x)^2' 
   plt.plot(x, y, label=label) 
 
   # 设置图片的右边框和上边框为不显示 
   ax.spines['right'].set_color('none') 
   ax.spines['top'].set_color('none') 
 
   # 挪动x，y轴的位置，也就是图片下边框和左边框的位置 
   # data表示通过值来设置x轴的位置，将x轴绑定在y=0的位置 
   ax.spines['bottom'].set_position(('data', 0)) 
   # axes表示以百分比的形式设置轴的位置，即将y轴绑定在x轴50%的位置 
   # ax.spines['left'].set_position(('axes', 0.5)) 
   ax.spines['left'].set_position(('data', 0)) 
   plt.title("sin&cos三角指数") 
   plt.legend(loc='upper right') 
   plt.show() 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.

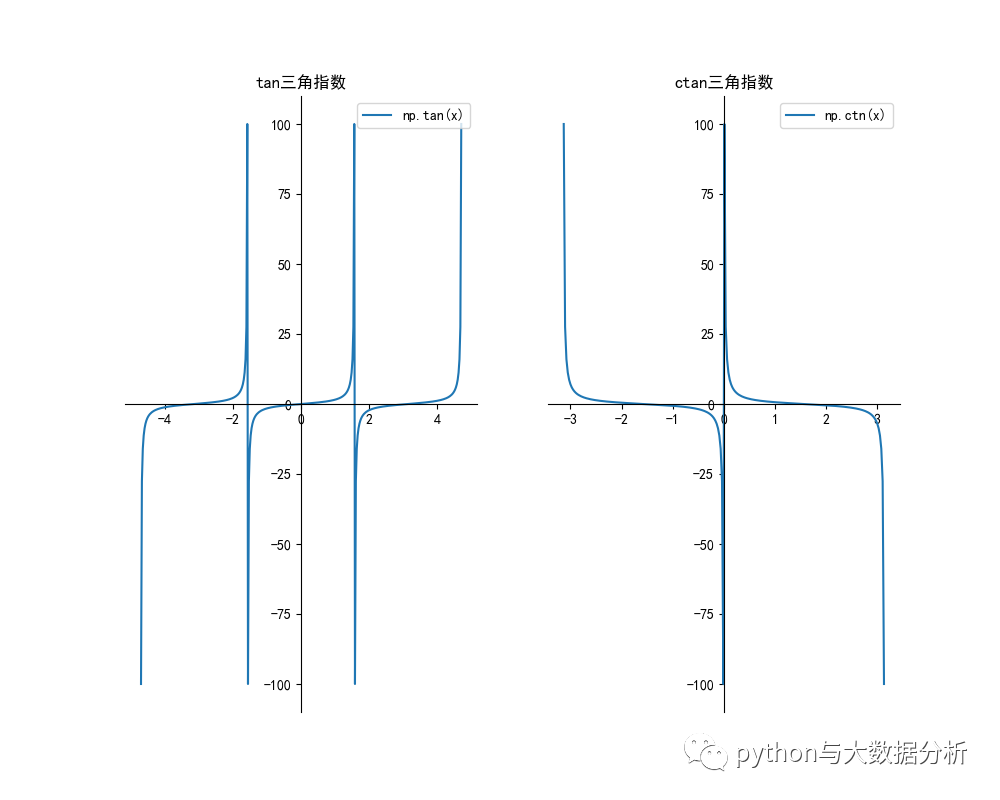
# 正切函数 ：y =tan x 
# 余切函数 ：y =cot x 
def tanctnfunction(): 
   #np.tan() 
   plt.figure(figsize=(10, 8)) 
   plt.subplot(1, 2, 1) 
   ax = plt.gca()  # 通过gca:get current axis得到当前轴 
   plt.rcParams['font.sans-serif'] = ['SimHei']  # 绘图中文 
   plt.rcParams['axes.unicode_minus'] = False  # 绘图负号 
   x = np.append(np.linspace(-np.pi*3/2+0.01, -np.pi/2-0.01, 120),np.linspace(-np.pi/2+0.01, np.pi/2-0.01, 120)) 
   x = np.append(x,np.linspace(np.pi/2+0.01, np.pi*3/2-0.01, 120)) 
   y = np.tan(x) 
   label = 'np.tan(x)' 
   plt.plot(x, y, label=label) 
 
 
   # 设置图片的右边框和上边框为不显示 
   ax.spines['right'].set_color('none') 
   ax.spines['top'].set_color('none') 
 
   # 挪动x，y轴的位置，也就是图片下边框和左边框的位置 
   # data表示通过值来设置x轴的位置，将x轴绑定在y=0的位置 
   ax.spines['bottom'].set_position(('data', 0)) 
   # axes表示以百分比的形式设置轴的位置，即将y轴绑定在x轴50%的位置 
   # ax.spines['left'].set_position(('axes', 0.5)) 
   ax.spines['left'].set_position(('data', 0)) 
   plt.title("tan三角指数") 
   plt.legend(loc='upper right') 
 
 
   plt.subplot(1, 2, 2) 
   ax = plt.gca()  # 通过gca:get current axis得到当前轴 
   plt.rcParams['font.sans-serif'] = ['SimHei']  # 绘图中文 
   plt.rcParams['axes.unicode_minus'] = False  # 绘图负号 
   x = np.append(np.linspace(-np.pi+ 0.01, - 0.01, 120), 
              np.linspace( 0.01, np.pi - 0.01, 120)) 
   y = 1/np.tan(x) 
   label = 'np.ctn(x)' 
   plt.plot(x, y, label=label) 
   # 设置图片的右边框和上边框为不显示 
   ax.spines['right'].set_color('none') 
   ax.spines['top'].set_color('none') 
 
   # 挪动x，y轴的位置，也就是图片下边框和左边框的位置 
   # data表示通过值来设置x轴的位置，将x轴绑定在y=0的位置 
   ax.spines['bottom'].set_position(('data', 0)) 
   # axes表示以百分比的形式设置轴的位置，即将y轴绑定在x轴50%的位置 
   ax.spines['left'].set_position(('axes', 0.5)) 
   #ax.spines['left'].set_position(('data', 0)) 
   plt.title("ctan三角指数") 
   plt.legend(loc='upper right') 
   plt.show() 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.

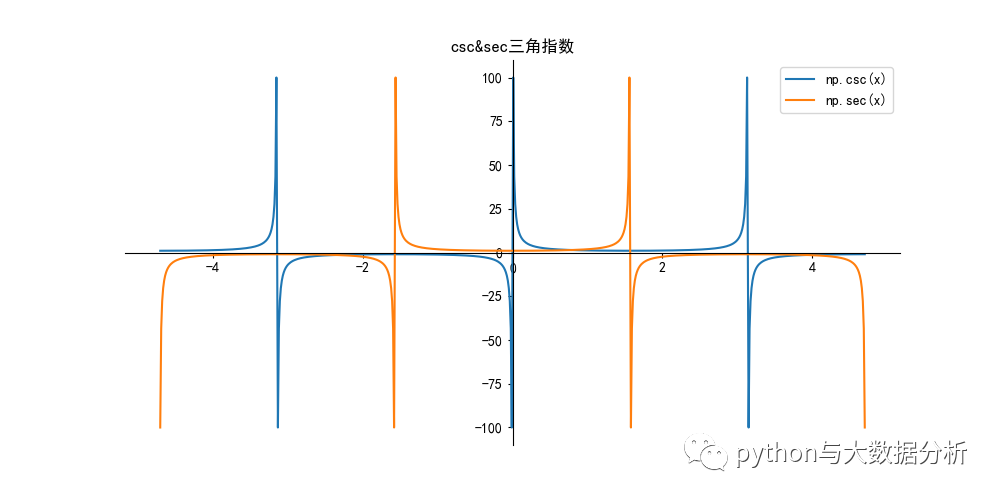
# 正割函数 ：y =sec x = 1/cos(x) 
# 余割函数 ：y =csc x = 1/sin(x) 
def seccscfunction(): 
   plt.figure(figsize=(10, 5)) 
   ax = plt.gca()  # 通过gca:get current axis得到当前轴 
   plt.rcParams['font.sans-serif'] = ['SimHei']  # 绘图中文 
   plt.rcParams['axes.unicode_minus'] = False  # 绘图负号 
   #x = np.linspace(-np.pi*2, np.pi*2, 200) 
   x = np.append(np.linspace(-np.pi * 3 / 2 + 0.01, -np.pi - 0.01, 120), 
              np.linspace(-np.pi + 0.01, -np.pi / 2 - 0.01, 120)) 
   x = np.append(x, np.linspace(-np.pi / 2 + 0.01,  - 0.01, 120)) 
   x = np.append(x, np.linspace(0.01, np.pi  / 2 - 0.01, 120)) 
   x = np.append(x, np.linspace(np.pi / 2 + 0.01, np.pi  - 0.01, 120)) 
   x = np.append(x, np.linspace(np.pi + 0.01, np.pi * 3 / 2 - 0.01, 120)) 
   y = 1/np.sin(x) 
   label = 'np.csc(x)' 
   plt.plot(x, y, label=label) 
   y = 1/np.cos(x) 
   label = 'np.sec(x)' 
   plt.plot(x, y, label=label) 
 
   # 设置图片的右边框和上边框为不显示 
   ax.spines['right'].set_color('none') 
   ax.spines['top'].set_color('none') 
 
   # 挪动x，y轴的位置，也就是图片下边框和左边框的位置 
   # data表示通过值来设置x轴的位置，将x轴绑定在y=0的位置 
   ax.spines['bottom'].set_position(('data', 0)) 
   # axes表示以百分比的形式设置轴的位置，即将y轴绑定在x轴50%的位置 
   # ax.spines['left'].set_position(('axes', 0.5)) 
   ax.spines['left'].set_position(('data', 0)) 
   plt.title("csc&sec三角指数") 
   plt.legend(loc='upper right') 
   plt.show() 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.

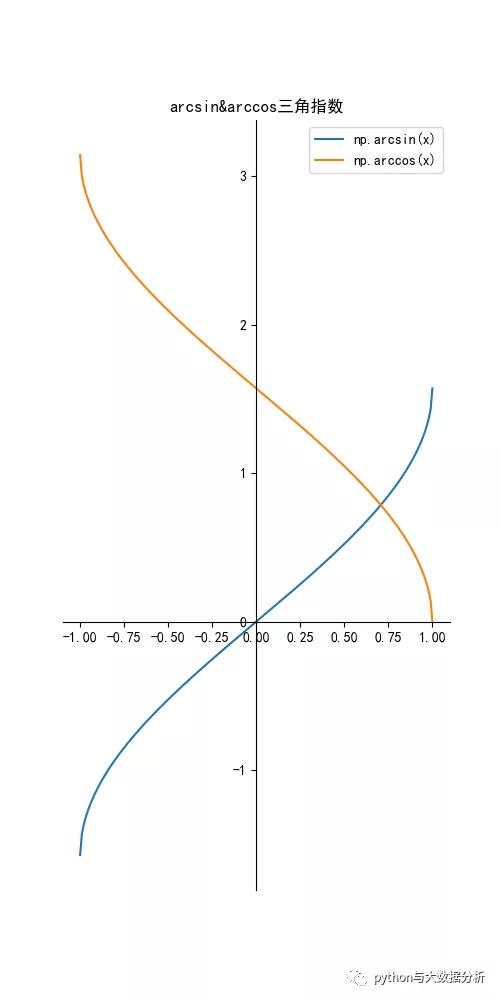
ef arcsincosfunction(): 
   plt.figure(figsize=(5, 10)) 
   ax = plt.gca()  # 通过gca:get current axis得到当前轴 
   plt.rcParams['font.sans-serif'] = ['SimHei']  # 绘图中文 
   plt.rcParams['axes.unicode_minus'] = False  # 绘图负号 
   x = np.linspace(-1, 1, 200) 
 
   y = np.arcsin(x) 
   label = 'np.arcsin(x)' 
   plt.plot(x, y, label=label) 
   y = np.arccos(x) 
   label = 'np.arccos(x)' 
   plt.plot(x, y, label=label) 
 
   # 设置图片的右边框和上边框为不显示 
   ax.spines['right'].set_color('none') 
   ax.spines['top'].set_color('none') 
 
   # 挪动x，y轴的位置，也就是图片下边框和左边框的位置 
   # data表示通过值来设置x轴的位置，将x轴绑定在y=0的位置 
   ax.spines['bottom'].set_position(('data', 0)) 
   # axes表示以百分比的形式设置轴的位置，即将y轴绑定在x轴50%的位置 
   # ax.spines['left'].set_position(('axes', 0.5)) 
   ax.spines['left'].set_position(('data', 0)) 
   plt.title("arcsin&arccos三角指数") 
   plt.legend(loc='upper right') 
   plt.show() 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.

# 反正切函数 
#  正切函数y=tan x在（-π/2，π/2）上的反函数，叫做反正切函数。记作arctanx，表示一个正切值为x的角，该角的范围在（-π/2，π/2）区间内。 
#  定义域R，值域（-π/2，π/2）。 
#   numpy.arctan() 
# 反余切函数 
#  余切函数y=cot x在（0，π）上的反函数，叫做反余切函数。记作arccotx，表示一个余切值为x的角，该角的范围在（0，π）区间内。 
#  定义域R，值域（0，π）。 
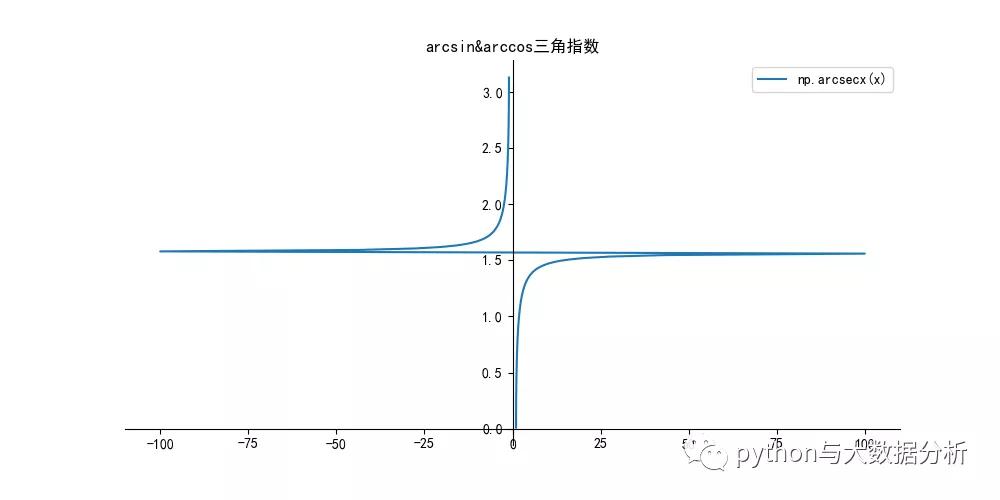
# 反正割函数 
#   正割函数 ：y =sec x = 1/cos(x) 
#  正割函数y=sec x在[0，π/2）U（π/2，π]上的反函数，叫做反正割函数。记作arcsecx，表示一个正割值为x的角，该角的范围在[0，π/2）U（π/2，π]区间内。 
#  定义域（-∞，-1]U[1，+∞），值域[0，π/2）U（π/2，π]。 
# 反余割函数 
#   余割函数 ：y =csc x = 1/sin(x) 
#  余割函数y=csc x在[-π/2，0）U（0，π/2]上的反函数，叫做反余割函数。记作arccscx，表示一个余割值为x的角，该角的范围在[-π/2，0）U（0，π/2]区间内。 
#  定义域（-∞，-1]U[1，+∞），值域[-π/2，0）U（0，π/2]。 
def arccscfunction(): 
   plt.figure(figsize=(10, 5)) 
   ax = plt.gca()  # 通过gca:get current axis得到当前轴 
   plt.rcParams['font.sans-serif'] = ['SimHei']  # 绘图中文 
   plt.rcParams['axes.unicode_minus'] = False  # 绘图负号 
   x = np.append(np.linspace(0.01, np.pi / 2 - 0.01, 120), 
              np.linspace(np.pi/2+0.01, np.pi  - 0.01, 120)) 
   y = 1/np.cos(x) 
   # 正割函数 sec(x)=1/cos(x) 
   # 反正割函数 颠倒x,y值即可 
   label = 'np.arcsecx(x)' 
   plt.plot(y, x, label=label) 
 
   # 设置图片的右边框和上边框为不显示 
   ax.spines['right'].set_color('none') 
   ax.spines['top'].set_color('none') 
 
   # 挪动x，y轴的位置，也就是图片下边框和左边框的位置 
   # data表示通过值来设置x轴的位置，将x轴绑定在y=0的位置 
   ax.spines['bottom'].set_position(('data', 0)) 
   # axes表示以百分比的形式设置轴的位置，即将y轴绑定在x轴50%的位置 
   # ax.spines['left'].set_position(('axes', 0.5)) 
   ax.spines['left'].set_position(('data', 0)) 
   plt.title("arcsin&arccos三角指数") 
   plt.legend(loc='upper right') 
   plt.show() 
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.