引入主题,看代码
我们先来看看以下程序
- #include <iostream>
- using namespace std;
- struct st1
- {
- char a ;
- int b ;
- short c ;
- };
- struct st2
- {
- short c ;
- char a ;
- int b ;
- };
- int main()
- {
- cout<<"sizeof(st1) -> "<<sizeof(st1)<<endl;
- cout<<"sizeof(st2) -> "<<sizeof(st2)<<endl;
- return 0 ;
- }
编译的结果如下:
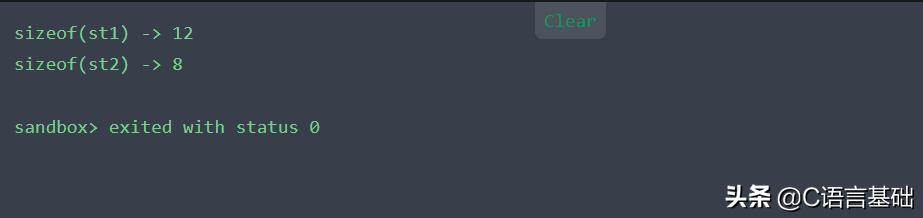
问题来了,两个结构体的内容一样,只是换了个位置,为什么sizeof(st)的时候大小不一样呢?
没错,这正是因为内存对齐的影响,导致的结果不同。对于我们大部分程序员来说,都不知道内存是怎么分布的。
实际上因为这是编译器该干的活,编译器把程序中的每个数据单元安排在合适的位置上,导致了相同的变量,不同声明顺序的结构体大小的不同。
几种类型数据所占字节数
int,long int,short int的宽度和机器字长及编译器有关,但一般都有以下规则(ANSI/ISO制订的)
- sizeof(short int) <= sizeof(int)
- sizeof(int) <= sizeof(long int)
- short int至少应为16位(2字节)
- long int至少应为32位
数据类型16位编译器32位编译器64位编译器char1字节1字节1字节char*2字节4字节8字节short int2字节2字节2字节int2字节4字节4字节unsigned int2字节4字节4字节float4字节4字节4字节double8字节8字节8字节long4字节4字节8字节long long8字节8字节8字节unsigned long4字节4字节8字节
什么是对齐
现代计算机中内存空间都是按照byte划分的,从理论上讲似乎对任何类型的变量的访问都可以从任何地址开始,但实际情况是在访问特定变量的时候经常在特定的内存地址访问。
所以这就需要各类型数据按照一定的规则在空间上排列,而不是顺序的一个接一个的排放,这就是对齐。内存对齐又分为自然对齐和规则对齐。
对于内存对齐问题,主要存在于struct和union等复合结构在内存中的分布情况,许多实际的计算机系统对基本类型数据在内存中存放的位置有限制,它们要求这些数据的首地址的值是某个数M(通常是4或8);
对于内存对齐,主要是为了提高程序的性能,数据结构,特别是栈,应尽可能在自然边界上对齐,经过对齐后,cpu的内存访问速度大大提升。
自然对齐
指的是将对应变量类型存入对应地址值的内存空间,即数据要根据其数据类型存放到以其数据类型为倍数的地址处。
例如char类型占1个字节空间,1的倍数是所有数,因此可以放置在任何允许地址处,而int类型占4个字节空间,以4为倍数的地址就有0,4,8等。编译器会优先按照自然对齐进行数据地址分配。
规则对齐
以结构体为例就是在自然对齐后,编译器将对自然对齐产生的空隙内存填充无效数据,且填充后结构体占内存空间为结构体内占内存空间最大的数据类型成员变量的整数倍。
实验对比
首先看这个结构体
- typedef struct test_32
- {
- char a;
- short b;
- short c;
- char d;
- }test_32;
首先按照自然对齐,得到如下图的内存分布位置,第一个格子地址为0,后面递增。

编译器将对空白处进行无效数据填充,最后将得到此结构体占内存空间为8字节,这个数值也是最大的数据类型short的2个字节的整数倍。
如果稍微调换一下位置的结构体
- typedef struct test_32
- {
- char a;
- char b;
- short c;
- short d;
- }test_32;
同样按照自然对齐如下图分布

可以看到按照自然对齐,变量之间没有出现间隙,所以规则对齐也不用进行填充,而这里有颜色的方格有6个,也就是6个字节
按照规则对齐,6字节是此结构体中最大数据类型short的整数倍,因此此结构体为6字节,后面的空白不需理会,可以实际编译一下运行,结果和分析一致为6个字节。
double的情况
我们知道32位处理器一次只能处理32位也就是4个字节的数据,而double是8字节数据类型,这要怎么处理呢?
如果是64位处理器,8字节数据可以一次处理完毕,而在32位处理器下,为了也能处理double8字节数据,在处理的时候将会把double拆分成两个4字节数进行处理,从这里就会出现一种情况如下:
- typedef struct test_32
- {
- char a;
- char b;
- double c;
- }test_32;
这个结构体在32位下所占内存空间为12字节,只能拆分成两个4字节进行处理,所以这里规则对齐将判定该结构体最大数据类型长度为4字节,因此总长度为4字节的整数倍,也就是12字节。
这个结构体在64位环境下所占内存空间为16字节,而64位判定最大为8字节,所以结果也是8字节的整数倍:16字节。这里的结构体中的double没有按照自然对齐放置到理论上的8字节倍数地址处,我认为这里编译器也有根据规则对齐做出相应的优化,节省了4个多余字节。
这部分各位可以按照上述规则自行分析测试。
数组
对齐值为:min(数组元素类型,指定对齐长度)。但数组中的元素是连续存放,存放时还是按照数组实际的长度。
如char t[9],对齐长度为1,实际占用连续的9byte。然后根据下一个元素的对齐长度决定在下一个元素之前填补多少byte。
嵌套的结构体
假设
- struct A
- {
- ......
- struct B b;
- ......
- };
对于B结构体在A中的对齐长度为:min(B结构体的对齐长度,指定的对齐长度)。
B结构体的对齐长度为:上述2种结构整体对齐规则中的对齐长度。举个例子
- #include <iostream>
- #include <cstdio>
- using namespace std;
- #pragma pack(8)
- struct Args
- {
- char ch;
- double d;
- short st;
- char rs[9];
- int i;
- } args;
- struct Argsa
- {
- char ch;
- Args test;
- char jd[10];
- int i;
- }arga;
- int main()
- {
- cout<<"Args:"<<sizeof(args)<<endl;
- cout<<""<<(unsigned long)&args.i-(unsigned long)&args.rs<<endl;
- cout<<"Argsa:"<<sizeof(arga)<<endl;
- cout<<"Argsa:"<<(unsigned long)&arga.i -(unsigned long)&arga.jd<<endl;
- cout<<"Argsa:"<<(unsigned long)&arga.jd-(unsigned long)&arga.test<<endl;
- return 0;
- }
输出结果:
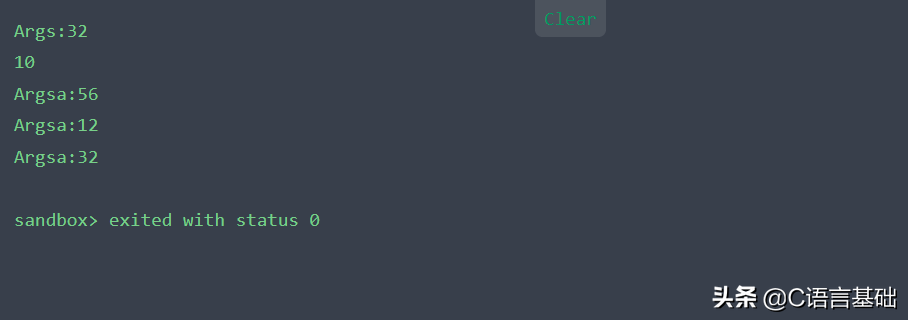
改成#pragma pack (16)结果一样,这个例子证明了三点:
- 对齐长度长于struct中的类型长度最长的值时,设置的对齐长度等于无用
- 数组对齐的长度是按照数组成员类型长度来比对的
- 嵌套的结构体中,所包含的结构体的对齐长度是结构体的对齐长度
指针
主要是因为32位和64位机寻址上,来看看例子
- //编译器:https://tool.lu/coderunner/
- //来源:技术让梦想更伟大
- //作者:李肖遥
- #include <iostream>
- #include <cstdio>
- using namespace std;
- #pragma pack(4)
- struct Args
- {
- int i;
- double d;
- char *p;
- char ch;
- int *pi;
- }args;
- int main()
- {
- cout<<"args length:"<<sizeof(args)<<endl;
- cout<<"args1:"<<(unsigned long)&args.ch-(unsigned long)&args.p<<endl;
- cout<<"args2:"<<(unsigned long)&args.pi-(unsigned long)&args.ch<<endl;
- return 0;
- }
结果如下
pack48length3240args188args248
内存对齐的规则
1.数据成员对齐规则
结构或联合的数据成员,第一个数据成员放在offset为0的地方,以后每个数据成员的对齐按照#pragma pack指定的数值和这个数据成员自身长度中,比较小的那个进行。
例如struct a里存有struct b,b里有char,int ,double等元素,那b应该从8的整数倍开始存储。
2.结构体作为成员
如果一个结构里有某些结构体成员,则结构体成员要从其内部"最宽基本类型成员"的整数倍地址开始存储。
在数据成员完成各自对齐之后,结构或联合本身也要进行对齐,对齐将按照#pragma pack指定的数值和结构或联合最大数据成员长度中,比较小的那个进行。
3.1&2的情况下注意
当#pragma pack的n值等于或超过所有数据成员长度的时候,这个n值的大小将不产生任何效果。
#pragma pack()用法详解
- 作用
指定结构体、联合以及类成员的packing alignment;
- 语法
#pragma pack( [show] | [push | pop] [, identifier], n )
- 说明
- pack提供数据声明级别的控制,对定义不起作用;
- 调用pack时不指定参数,n将被设成默认值;
- 一旦改变数据类型的alignment,直接效果就是占用memory的减少,但是performance会下降;
- 语法具体分析
1.show:可选参数
显示当前packing aligment的字节数,以warning message的形式被显示;
2.push:可选参数
将当前指定的packing alignment数值进行压栈操作,这里的栈是the internal compiler stack,同时设置当前的packing alignment为n;如果n没有指定,则将当前的packing alignment数值压栈;
3.pop:可选参数
从internal compiler stack中删除最顶端的record;如果没有指定n,则当前栈顶record即为新的packing alignment数值;如果指定了n,则n将成为新的packing aligment数值;如果指定了identifier,则internal compiler stack中的record都将被pop直到identifier被找到,然后pop出identitier,同时设置packing alignment数值为当前栈顶的record;如果指定的identifier并不存在于internal compiler stack,则pop操作被忽略;
4.identifier:可选参数
当同push一起使用时,赋予当前被压入栈中的record一个名称;当同pop一起使用时,从internal compiler stack中pop出所有的record直到identifier被pop出,如果identifier没有被找到,则忽略pop操作;
5.n:可选参数
指定packing的数值,以字节为单位;缺省数值是8,合法的数值分别是1、2、4、8、16
例子
- #include<stddef.h>
- #include<iostream>
- using namespace std;
- #pragma pack(4)
- struct m
- {
- int a;
- short b;
- int c;
- };
- int main()
- {
- cout <<"结构体m的大小:"<< sizeof(m) << endl;
- cout << endl;
- // 获得成员a相对于m储存地址的偏移量
- int offset_b = offsetof(struct m, a);
- cout <<"a相对于m储存地址的偏移量:"<< offset_b << endl;
- system("pause");
- return 0;
- }

从运行结果来看我们可以证实上面内存对齐规则的第一条:第一个数据成员放在offset为0的地方。
现在咱来看看上面结构体是如何内存对齐的;先用代码打印它们每个数据成员的存储地址的偏移量
- #include<stddef.h>
- #include<iostream>
- using namespace std;
- #pragma pack(4)
- struct m
- {
- int a;
- short b;
- int c;
- };
- int main()
- {
- cout <<"结构体m的大小:"<< sizeof(m) << endl;
- cout << endl;
- int offset_b = offsetof(struct m, a);// 获得成员a相对于m储存地址的偏移量
- int offset_b1 = offsetof(struct m, b);// 获得成员a相对于m储存地址的偏移量
- int offset_b2 = offsetof(struct m, c);// 获得成员a相对于m储存地址的偏移量
- cout <<"a相对于m储存地址的偏移量:"<< offset_b << endl;
- cout << "b相对于m储存地址的偏移量:" << offset_b1 << endl;
- cout << "c相对于m储存地址的偏移量:" << offset_b2 << endl;
- //system("pause");
- return 0;
- }

在此c在结构体中偏移量为8加上它自身(int)4个字节,刚好是12(c的开始位置为8,所以要加它的4个字节)
上面内存结束为11,因为0-11,12是最大对齐数的整数倍,故取其临近的倍数,所以就取4的整数倍即12;
上图中我用连续的数组来模仿内存,如图是它们的内存对齐图;
如果将最大内存对齐数改为8,它将验证内存对齐规则中的第3条。
如果将其改为2,会发生什么:我们来看看:
- #include<stddef.h>
- #include<iostream>
- using namespace std;
- #pragma pack(2)
- struct m
- {
- int a;
- short b;
- int c;
- };
- int main()
- {
- cout <<"结构体m的大小:"<< sizeof(m) << endl;
- cout << endl;
- int offset_b = offsetof(struct m, a);// 获得成员a相对于m储存地址的偏移量
- int offset_b1 = offsetof(struct m, b);// 获得成员a相对于m储存地址的偏移量
- int offset_b2 = offsetof(struct m, c);// 获得成员a相对于m储存地址的偏移量
- cout <<"a相对于m储存地址的偏移量:"<< offset_b << endl;
- cout << "b相对于m储存地址的偏移量:" << offset_b1 << endl;
- cout << "c相对于m储存地址的偏移量:" << offset_b2 << endl;
- //system("pause");
- return 0;
- }
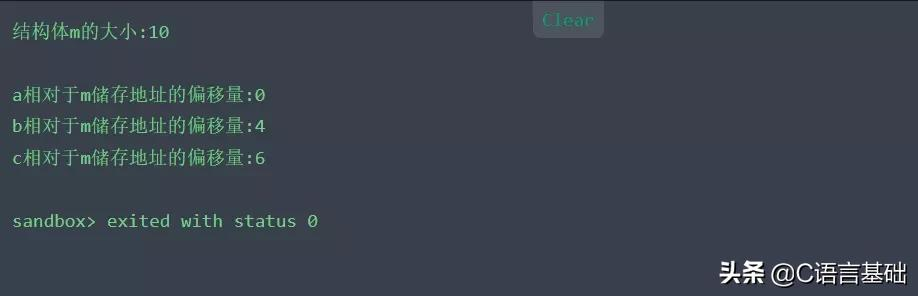
对于这个结果,我们按刚才第一个例子我所分析的过程来分析这段代码,得到的是10;
故当我们将#pragma pack的n值小于所有数据成员长度的时候,结果将改变。
对齐的作用和原因
各个硬件平台对存储空间的处理上有很大的不同。如果不按照适合其平台要求对数据存放进行对齐,可能会在存取效率上带来损失。
比如有些平台每次读都是从偶地址开始,如果一个int型在32位地址存放在偶地址开始的地方,那么一个读周期就可以读出;
而如果存放在其地址开始的地方,就可能会需要2个读周期,并对两次读出的结果的高低字节进行拼凑才能得到该int数据。那么在读取效率上下降很多,这也是空间和时间的博弈。
CPU每次从内存中取出数据或者指令时,并非想象中的一个一个字节取出拼接的,而是根据自己的字长,也就是CPU一次能够处理的数据长度取出内存块。总之,CPU会以它“最舒服的”数据长度来读取内存数据
举个例子
如果有一个4字节长度的指令准备被读取进CPU处理,就会有两种情况出现:
4个字节起始地址刚好就在CPU读取的地址处,这种情况下,CPU可以一次就把这个指令读出,并执行,内存情况如下

而当4个字节按照如下图所示分布时
假设CPU还在同一个地址取数据,则取到第一个4字节单元得到了1、2字节的数据,但是这个数据不符合需要的数字,所以CPU就要在后续的内存中继续取值,这才取到后面的4字节单元得到3、4字节数据,从而和前面取到的1、2字节拼接成一个完整数据。
而本次操作进行了两次内存读取,考虑到CPU做大量的数据运算和操作,如果遇到这种情况很多的话,将会严重影响CPU的处理速度。
因此,系统需要进行内存对齐,而这项任务就交给编译器进行相应的地址分配和优化,编译器会根据提供参数或者目标环境进行相应的内存对齐。
什么时候需要进行内存对齐.
一般情况下都不需要对编译器进行的内存对齐规则进行修改,因为这样会降低程序的性能,除非在以下两种情况下:
这个结构需要直接被写入文件
这个结构需通过网络传给其他程序
对齐的实现
可以通知给编译器传递预编译指令,从而改变对指定数据的对齐方法。
- unsigned int calc_align(unsigned int n,unsigned align)
- {
- if ( n / align * align == n)
- return n;
- return (n / align + 1) * align;
- }
不过这种算法的效率很低,下面介绍一种高效率的数据对齐算法:
- unsigned int calc_align(unsigned int n,unsigned align)
- {
- return ((n + align - 1) & (~(align - 1)));
- }
这种算法的原理是:
(align-1) :对齐所需的对齐位,如:2字节对齐为1,4字节为11,8字节为111,16字节为1111...
(&~(align-1)) :将对齐位数据置位为0,其位为1
(n+(align-1)) & ~(align-1) :对齐后的数据
总结
通常,我们写程序的时候,不需要考虑对齐问题,编译器会替我们选择目标平台的对齐策略。但正因为我们没注意这个问题,导致编辑器对数据存放做了对齐,而我们如果不了解的话,就会对一些问题感到迷惑。所以知其然,更要知其所以然。好了,我们介绍到这里,下一期再见!