一篇学会使用 SwiftUI 创建万花尺-51CTO.COM

本文转载自微信公众号「Swift社区」，作者韦弦Zhy。转载本文请联系Swift社区公众号。

为了完成一些真正意义上的绘图工作，我将带您通过创建一个简单的带 SwiftUI 的 spirograph。“Spirograph”是一种玩具的商标名称，你把一支铅笔放在一个圆圈里，然后绕着另一个圆圈的圆周旋转，创造出各种几何图案，称为轮盘赌——就像赌场游戏一样。

这段代码包含一个非常具体的公式。我会解释的，但是如果你不感兴趣的话，跳过这一章是完全可以的——这只是为了好玩，这里没有介绍新的 Swift 或 SwiftUI。

我们的算法有四个输入：

内圈的半径。
外圈的半径。
虚拟笔与外圆中心的距离。
要画多少轮盘赌。这是可选的，但我认为它确实有助于显示算法工作时发生的情况。

因此，让我们开始吧：

struct Spirograph: Shape { 
    let innerRadius: Int 
    let outerRadius: Int 
    let distance: Int 
    let amount: CGFloat 
}

然后，我们从数据中准备三个值，从内半径和外半径的最大公约数(GCD)开始。计算两个数字的GCD通常是用Euclid算法完成的，它的形式稍微简化如下：

func gcd(_ a: Int,  _ b: Int) -> Int { 
    var a = a 
    var b = b 
    while b != 0 { 
        let temp = b 
        b = a % b 
        a = temp 
    } 
    return a 
}

把这个方法添加到Spirograph结构体中。

另外两个值是内半径和外半径之间的差异，以及我们需要执行多少步骤来绘制轮盘——这是360度乘以外半径除以最大公约数，再乘以我们的数量输入。我们所有的输入以整数形式提供时效果最好，但是在绘制轮盘赌时，我们需要使用CGFloat，因此我们还将创建输入的CGFloat副本。

现在将这个path(in:)方法添加到Spirograph结构体：

func path(in rect: CGRect) -> Path { 
    let divisor = gcd(innerRadius, outerRadius) 
    let outerRadius = CGFloat(self.outerRadius) 
    let innerRadius = CGFloat(self.innerRadius) 
    let distance = CGFloat(self.distance) 
    let difference = innerRadius - outerRadius 
    let endPoint = ceil(2 * CGFloat.pi * outerRadius / CGFloat(divisor)) * amount 
 
    // more code to come 
}

最后，我们可以通过循环从 0 到我们的终点来画轮盘赌，并放置在精确的 X/Y 坐标点。计算循环中给定点的 X/Y 坐标(称为“theta：θ”)是真正的数学来源，但老实说，我只是把维基百科上的标准方程式转换成 Swift ——这不是我梦寐以求的记忆!

X等于半径差乘以 θ 的余弦，再乘以半径差的余弦除以外半径乘以θ的距离。
Y等于半径差乘以 θ 的正弦，减去距离乘以半径差的正弦除以外半径乘以 θ。

这是核心算法，但我们要做两个小的改变：我们要分别将绘图矩形的一半宽度或高度添加到X和Y，使其在绘图空间中居中;如果 θ 为 0，即如果这是轮盘中绘制的第一个点，我们将我们的路径中调用move(to:)而不是addLine(to:)。

以下是path(in:)方法的最后一个代码——用以下内容替换// more code to come注释：

var path = Path() 
 
for theta in stride(from: 0, through: endPoint, by: 0.01) { 
    var x = difference * cos(theta) + distance * cos(difference / outerRadius * theta) 
    var y = difference * sin(theta) - distance * sin(difference / outerRadius * theta) 
 
    x += rect.width / 2 
    y += rect.height / 2 
 
    if theta == 0 { 
        path.move(to: CGPoint(x: x, y: y)) 
    } else { 
        path.addLine(to: CGPoint(x: x, y: y)) 
    } 
} 
 
return path

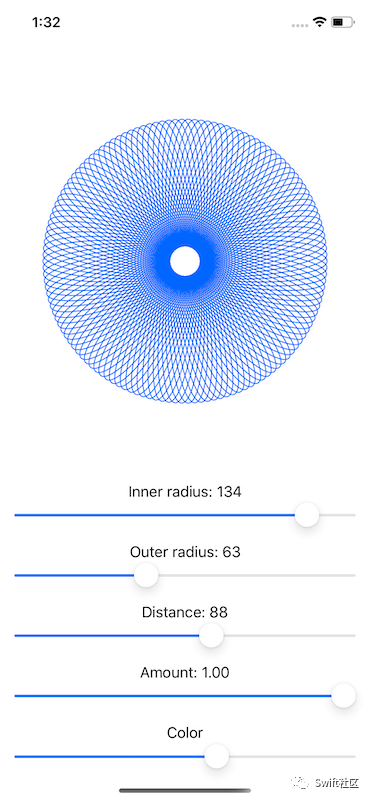
我意识到这有很多繁重的数学，但回报即将到来：我们现在可以在视图中使用该形状，添加各种滑块来控制内半径、外半径、距离、数量，甚至颜色：

struct ContentView: View { 
    @State private var innerRadius = 125.0 
    @State private var outerRadius = 75.0 
    @State private var distance = 25.0 
    @State private var amount: CGFloat = 1.0 
    @State private var hue = 0.6 
 
    var body: some View { 
        VStack(spacing: 0) { 
            Spacer() 
 
            Spirograph(innerRadius: Int(innerRadius), outerRadius: Int(outerRadius), distance: Int(distance), amount: amount) 
                .stroke(Color(hue: hue, saturation: 1, brightness: 1), lineWidth: 1) 
                .frame(width: 300, height: 300) 
 
            Spacer() 
 
            Group { 
                Text("Inner radius: \(Int(innerRadius))") 
                Slider(value: $innerRadius, in: 10...150, step: 1) 
                    .padding([.horizontal, .bottom]) 
 
                Text("Outer radius: \(Int(outerRadius))") 
                Slider(value: $outerRadius, in: 10...150, step: 1) 
                    .padding([.horizontal, .bottom]) 
 
                Text("Distance: \(Int(distance))") 
                Slider(value: $distance, in: 1...150, step: 1) 
                    .padding([.horizontal, .bottom]) 
 
                Text("Amount: \(amount, specifier: "%.2f")") 
                Slider(value: $amount) 
                    .padding([.horizontal, .bottom]) 
 
                Text("Color") 
                Slider(value: $hue) 
                    .padding(.horizontal) 
            } 
        } 
    } 
}

这是很多代码，但我希望你花时间运行应用程序，并欣赏有多么美丽的轮盘。你所看到的其实只是一种轮盘赌形式，被称为 hypotrochoid ——通过对算法的小调整，你可以生成 epitrochoids 等，它们以不同的方式很漂亮。

在我结束之前，我想提醒你，这里使用的参数方程是数学标准，而不是我刚刚发明的东西——我真的去百度了关于 hypotrochoids[1] 的页面，并将它们转换为 Swift。

参考资料

[1]hypotrochoids: http://www.durangobill.com/Trochoids.html