使用 Python 进行数据预处理的标准化-python 数据标准化

标准化和规范化是机器学习和深度学习项目中大量使用的数据预处理技术之一。

[[411810]]

这些技术的主要作用

以类似的格式缩放所有数据，使模型的学习过程变得容易。
数据中的奇数值被缩放或归一化并且表现得像数据的一部分。

我们将通过 Python 示例深入讨论这两个概念。

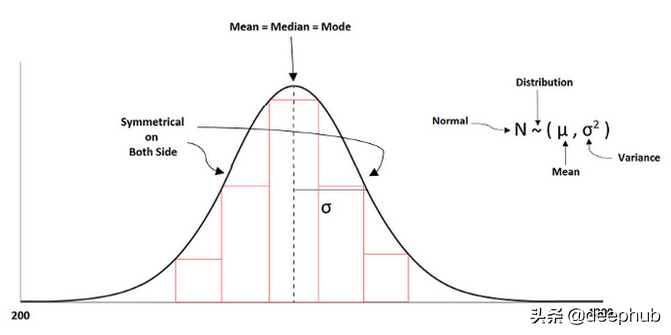
标准化

数据的基本缩放是使其成为标准，以便所有值都在共同范围内。在标准化中，数据的均值和方差分别为零和一。它总是试图使数据呈正态分布。

标准化公式如下所示：

z =(列的值 - 平均值)/标准偏差

机器学习中的一些算法试图让数据具有正态分布。但是，如果一个特征有更多的方差，而其他特征有低或单位方差，那么模型的学习将是不正确的，因为从一个特征到另一个特征的方差是有差异的。

正如我们上面讨论的，标准缩放的范围是“0”均值和“1”单位方差。

我们如何使用标准缩放?

要使用标准伸缩，我们需要从预处理类中导入它，如下所示:

from sklearn import preprocessing 
scaler = preprocessing.StandardScaler()

使用标准缩放的正确步骤是什么?

我们可以在 train-test split 之后使用标准缩放，因为如果我们在发生数据泄漏问题之前这样做，可能会导致模型不太可靠。如果我们在拆分之前进行缩放，那么从训练中学习的过程也可以在测试集上完成，这是我们不想要的。

让我们在sklearn库的帮助下看看拆分过程

from sklearn.model_selection import train_test_split 
X_train, X_test, y_train, y_test = train_test_split(x, 
y, train_size = 0.20, random_state = 42)

在此之后，我们可以使用标准缩放

from sklearn.preprocessing import StandardScaler 
sc = StandardScaler()  
X_train = sc.fit_transform(X_train)  
X_test = sc.transform(X_test)

让我们举一个 python 例子。

from sklearn import preprocessing 
import numpy as np 
#creating a training data 
X_train = np.array([[ 4., -3., 2.],  
[ 2., 2., 0.],  
[ 0., -6., 7.]]) 
 
#fit the training data 
scaler = preprocessing.StandardScaler().fit(X_train) 
scaler 
#output: 
StandardScaler()

现在，我们将检查训练数据中每个特征的均值和缩放比例。

scaler.mean_ 
#output: 
array([ 2., -2.33333333, 3.]) 
scaler.scale_ 
#output: 
array([1.63299316, 3.29983165, 2.94392029])

scale_属性找出特征之间的相对尺度，得到一个标准尺度，即零均值和单位方差。均值属性用来找出每个特征的均值。

现在，我们将转换缩放后的数据

X_scaled = scaler.transform(X_train) 
X_scaled 
#output: 
array([[ 1.22474487, -0.20203051, -0.33968311], 
[ 0. , 1.31319831, -1.01904933], 
[-1.22474487, -1.1111678 , 1.35873244]])

为了检查特征的零均值和单位方差，我们将找到均值和标准差。

X_scaled.mean(axis=0) 
#output: 
array([0., 0., 0.]) 
X_scaled.std(axis=0) 
#output: 
array([1., 1., 1.])

我们还可以在 MinMaxScaler 和 MaxAbsScaler 的帮助下进行范围缩放。

有时，我们在数据中存在影响算法建模的异常值，并且标准缩放器受到异常值的影响，其他方法如 min-max 和 max-abs 缩放器使数据在一定范围内。

MinMaxScaler

MinMaxScaler 是另一种在 [0,1] 范围内缩放数据的方法。它使数据保持原始形状并保留有价值的信息，而受异常值的影响较小。

python示例如下所示：

from sklearn import preprocessing 
import numpy as np 
#creating a training data 
X_train = np.array([[ 4., -3., 2.],  
[ 2., 2., 0.],  
[ 0., -6., 7.]]) 
min_max_scaler = preprocessing.MinMaxScaler() 
X_train_minmax = min_max_scaler.fit_transform(X_train) 
X_train_minmax 
#output: 
array([[1. , 0.375 , 0.28571429], 
[0.5 , 1. , 0. ], 
[0. , 0. , 1. ]])

我们可以在使用 MinMaxScaler 缩放后看到“0”到“1”范围内的数据。

MaxAbsScaler

这是另一种缩放方法，其中数据在 [-1,1] 的范围内。这种缩放的好处是它不会移动或居中数据并保持数据的稀疏性。

python示例如下所示：

from sklearn import preprocessing 
import numpy as np 
#creating a training data 
X_train = np.array([[ 4., -3., 2.],  
[ 2., 2., 0.],  
[ 0., -6., 7.]]) 
max_abs_scaler = preprocessing.MaxAbsScaler() 
X_train_maxabs = max_abs_scaler.fit_transform(X_train) 
X_train_maxabs 
#output: 
array([[ 1. , -0.5 , 0.28571429], 
[ 0.5 , 0.33333333, 0. ], 
[ 0. , -1. , 1. ]])

我们可以在使用 MaxAbsScaler 缩放后看到“-1”到“1”范围内的数据。

总结

数据的缩放是机器学习或深度学习的一个非常重要的部分。在本文中，MaxAbsScaler 在稀疏数据中很有用，而另一方面，标准缩放也可以用于稀疏数据，但也会由于过多的内存分配而给出值错误。