二叉树的统一迭代法
此时我们在二叉树:一入递归深似海,从此offer是路人中用递归的方式,实现了二叉树前中后序的遍历。
在二叉树:听说递归能做的,栈也能做!中用栈实现了二叉树前后中序的迭代遍历(非递归)。
之后我们发现迭代法实现的先中后序,其实风格也不是那么统一,除了先序和后序,有关联,中序完全就是另一个风格了,一会用栈遍历,一会又用指针来遍历。
实践过的同学,也会发现使用迭代法实现先中后序遍历,很难写出统一的代码,不像是递归法,实现了其中的一种遍历方式,其他两种只要稍稍改一下节点顺序就可以了。
其实针对三种遍历方式,使用迭代法是可以写出统一风格的代码!
重头戏来了,接下来介绍一下统一写法。
我们以中序遍历为例,在二叉树:听说递归能做的,栈也能做!中提到说使用栈的话,无法同时解决访问节点(遍历节点)和处理节点(将元素放进结果集)不一致的情况。
那我们就将访问的节点放入栈中,把要处理的节点也放入栈中但是要做标记。
如何标记呢,就是要处理的节点放入栈之后,紧接着放入一个空指针作为标记。 这种方法也可以叫做标记法。
迭代法中序遍历
中序遍历代码如下:(详细注释)
- class Solution {
- public:
- vector<int> inorderTraversal(TreeNode* root) {
- vector<int> result;
- stack<TreeNode*> st;
- if (root != NULL) st.push(root);
- while (!st.empty()) {
- TreeNode* node = st.top();
- if (node != NULL) {
- st.pop(); // 将该节点弹出,避免重复操作,下面再将右中左节点添加到栈中
- if (node->right) st.push(node->right); // 添加右节点(空节点不入栈)
- st.push(node); // 添加中节点
- st.push(NULL); // 中节点访问过,但是还没有处理,加入空节点做为标记。
- if (node->left) st.push(node->left); // 添加左节点(空节点不入栈)
- } else { // 只有遇到空节点的时候,才将下一个节点放进结果集
- st.pop(); // 将空节点弹出
- node = st.top(); // 重新取出栈中元素
- st.pop();
- result.push_back(node->val); // 加入到结果集
- }
- }
- return result;
- }
- };
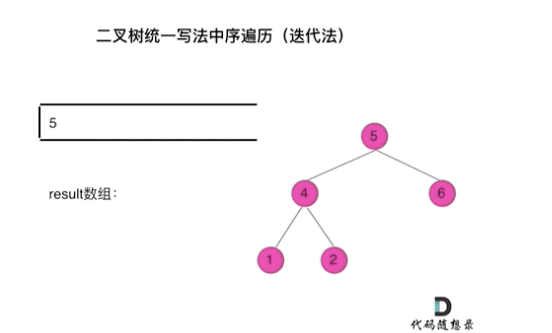
看代码有点抽象我们来看一下动画(中序遍历):
中序遍历迭代(统一写法)
动画中,result数组就是最终结果集。
可以看出我们将访问的节点直接加入到栈中,但如果是处理的节点则后面放入一个空节点, 这样只有空节点弹出的时候,才将下一个节点放进结果集。
此时我们再来看前序遍历代码。
迭代法前序遍历
迭代法前序遍历代码如下:(注意此时我们和中序遍历相比仅仅改变了两行代码的顺序)
- class Solution {
- public:
- vector<int> preorderTraversal(TreeNode* root) {
- vector<int> result;
- stack<TreeNode*> st;
- if (root != NULL) st.push(root);
- while (!st.empty()) {
- TreeNode* node = st.top();
- if (node != NULL) {
- st.pop();
- if (node->right) st.push(node->right); // 右
- if (node->left) st.push(node->left); // 左
- st.push(node); // 中
- st.push(NULL);
- } else {
- st.pop();
- node = st.top();
- st.pop();
- result.push_back(node->val);
- }
- }
- return result;
- }
- };
迭代法后序遍历
后续遍历代码如下:(注意此时我们和中序遍历相比仅仅改变了两行代码的顺序)
- class Solution {
- public:
- vector<int> postorderTraversal(TreeNode* root) {
- vector<int> result;
- stack<TreeNode*> st;
- if (root != NULL) st.push(root);
- while (!st.empty()) {
- TreeNode* node = st.top();
- if (node != NULL) {
- st.pop();
- st.push(node); // 中
- st.push(NULL);
- if (node->right) st.push(node->right); // 右
- if (node->left) st.push(node->left); // 左
- } else {
- st.pop();
- node = st.top();
- st.pop();
- result.push_back(node->val);
- }
- }
- return result;
- }
- };
总结
此时我们写出了统一风格的迭代法,不用在纠结于前序写出来了,中序写不出来的情况了。
但是统一风格的迭代法并不好理解,而且想在面试直接写出来还有难度的。
所以大家根据自己的个人喜好,对于二叉树的前中后序遍历,选择一种自己容易理解的递归和迭代法。
其他语言版本
Java:迭代法前序遍历代码如下:
- class Solution {
- public List<Integer> preorderTraversal(TreeNode root) {
- List<Integer> result = new LinkedList<>();
- Stack<TreeNode> st = new Stack<>();
- if (root != null) st.push(root);
- while (!st.empty()) {
- TreeNode node = st.peek();
- if (node != null) {
- st.pop(); // 将该节点弹出,避免重复操作,下面再将右中左节点添加到栈中
- if (node.right!=null) st.push(node.right); // 添加右节点(空节点不入栈)
- if (node.left!=null) st.push(node.left); // 添加左节点(空节点不入栈)
- st.push(node); // 添加中节点
- st.push(null); // 中节点访问过,但是还没有处理,加入空节点做为标记。
- } else { // 只有遇到空节点的时候,才将下一个节点放进结果集
- st.pop(); // 将空节点弹出
- node = st.peek(); // 重新取出栈中元素
- st.pop();
- result.add(node.val); // 加入到结果集
- }
- }
- return result;
- }
- }
迭代法中序遍历代码如下:
- class Solution {
- public List<Integer> inorderTraversal(TreeNode root) {
- List<Integer> result = new LinkedList<>();
- Stack<TreeNode> st = new Stack<>();
- if (root != null) st.push(root);
- while (!st.empty()) {
- TreeNode node = st.peek();
- if (node != null) {
- st.pop(); // 将该节点弹出,避免重复操作,下面再将右中左节点添加到栈中
- if (node.right!=null) st.push(node.right); // 添加右节点(空节点不入栈)
- st.push(node); // 添加中节点
- st.push(null); // 中节点访问过,但是还没有处理,加入空节点做为标记。
- if (node.left!=null) st.push(node.left); // 添加左节点(空节点不入栈)
- } else { // 只有遇到空节点的时候,才将下一个节点放进结果集
- st.pop(); // 将空节点弹出
- node = st.peek(); // 重新取出栈中元素
- st.pop();
- result.add(node.val); // 加入到结果集
- }
- }
- return result;
- }
- }
迭代法后序遍历代码如下:
- class Solution {
- public List<Integer> postorderTraversal(TreeNode root) {
- List<Integer> result = new LinkedList<>();
- Stack<TreeNode> st = new Stack<>();
- if (root != null) st.push(root);
- while (!st.empty()) {
- TreeNode node = st.peek();
- if (node != null) {
- st.pop(); // 将该节点弹出,避免重复操作,下面再将右中左节点添加到栈中
- st.push(node); // 添加中节点
- st.push(null); // 中节点访问过,但是还没有处理,加入空节点做为标记。
- if (node.right!=null) st.push(node.right); // 添加右节点(空节点不入栈)
- if (node.left!=null) st.push(node.left); // 添加左节点(空节点不入栈)
- } else { // 只有遇到空节点的时候,才将下一个节点放进结果集
- st.pop(); // 将空节点弹出
- node = st.peek(); // 重新取出栈中元素
- st.pop();
- result.add(node.val); // 加入到结果集
- }
- }
- return result;
- }
- }
Python:
迭代法前序遍历:
- class Solution:
- def preorderTraversal(self, root: TreeNode) -> List[int]:
- result = []
- st= []
- if root:
- st.append(root)
- while st:
- node = st.pop()
- if node != None:
- if node.right: #右
- st.append(node.right)
- if node.left: #左
- st.append(node.left)
- st.append(node) #中
- st.append(None)
- else:
- node = st.pop()
- result.append(node.val)
- return result
迭代法中序遍历:
- class Solution:
- def inorderTraversal(self, root: TreeNode) -> List[int]:
- result = []
- st = []
- if root:
- st.append(root)
- while st:
- node = st.pop()
- if node != None:
- if node.right: #添加右节点(空节点不入栈)
- st.append(node.right)
- st.append(node) #添加中节点
- st.append(None) #中节点访问过,但是还没有处理,加入空节点做为标记。
- if node.left: #添加左节点(空节点不入栈)
- st.append(node.left)
- else: #只有遇到空节点的时候,才将下一个节点放进结果集
- node = st.pop() #重新取出栈中元素
- result.append(node.val) #加入到结果集
- return result
迭代法后序遍历:
- class Solution:
- def postorderTraversal(self, root: TreeNode) -> List[int]:
- result = []
- st = []
- if root:
- st.append(root)
- while st:
- node = st.pop()
- if node != None:
- st.append(node) #中
- st.append(None)
- if node.right: #右
- st.append(node.right)
- if node.left: #左
- st.append(node.left)
- else:
- node = st.pop()
- result.append(node.val)
- return result
旧文链接:二叉树:前中后序迭代方式的写法就不能统一一下么?