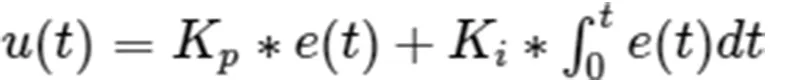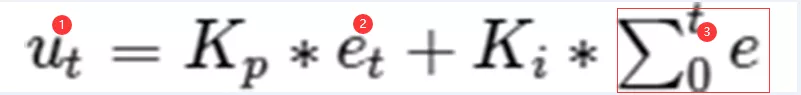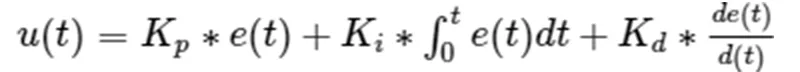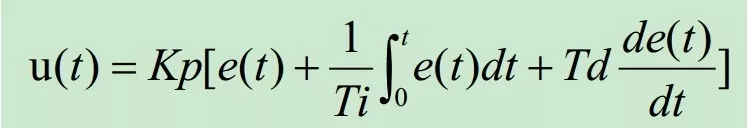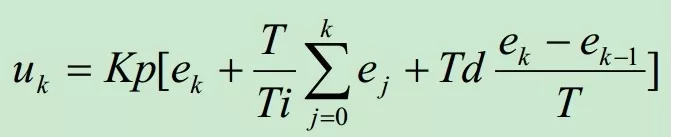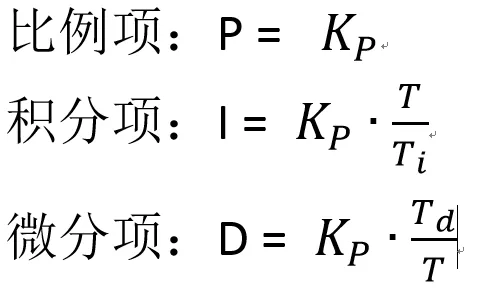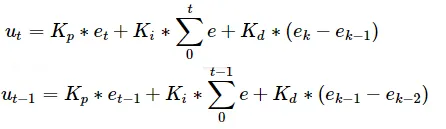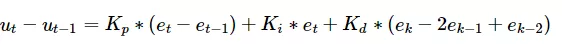1、引入PID
电机控制
这样是没有反馈的,也就是说我们完全相信输入的数字,且是理想化的模型,比如输入占空比为50%的25Kz的PWM,车轮速度为1m/s,实际产品中会受到各种这样的影响,比如地面阻力,风阻等等,同样输入占空比为50%的25Kz的PWM,车轮的速度并不是1m/s。
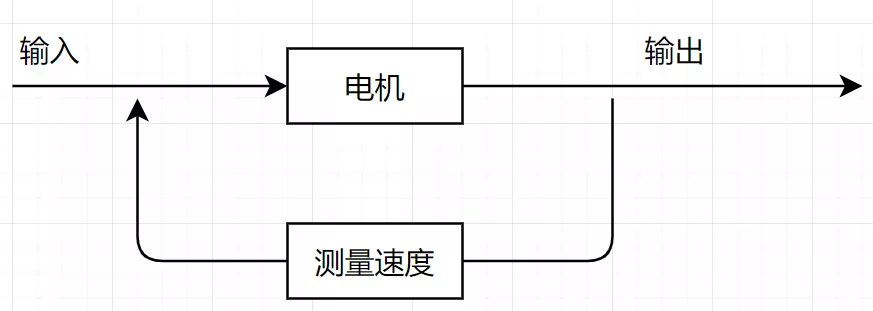
这时候我们就引入测量单元,也就是反馈系统。
这个时候,最常见的反馈就是:直接使用反馈值。简单的例子,属于数值X和输出数值y的数学公式是:y=2x,这是这最见的关系。假设我们输入7,测量结果是5,那么我们就直接将输入修改为7+2*(7-5)=11。也就是我们一次直接调整到位。这样调节过于简单粗暴,因为我们直接将输入修改为11,有可能输出直接变成6,超过预期值了。这时候就自然而然的想到多次调节,每次只增加一点,然后测量速度,看一下是否达标。
这就是比例调节Kp。
2、比例调节
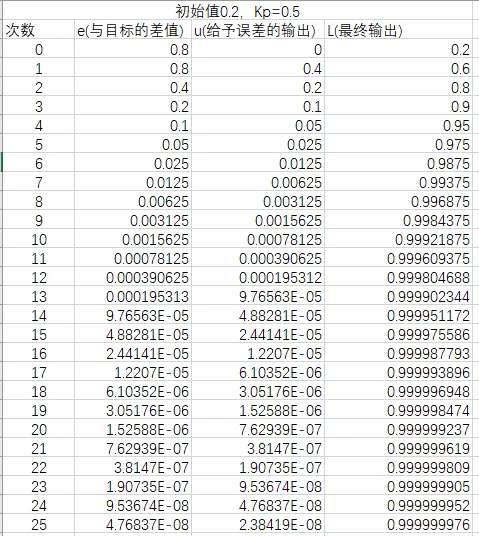
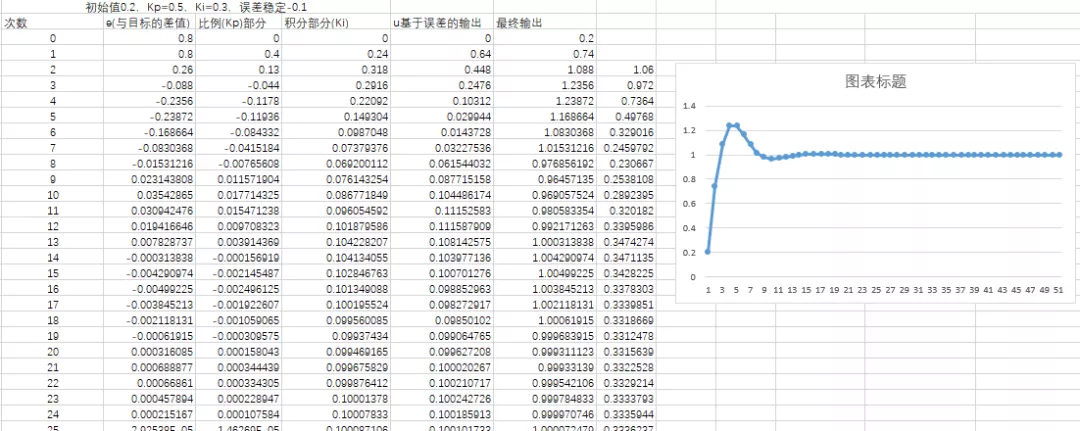
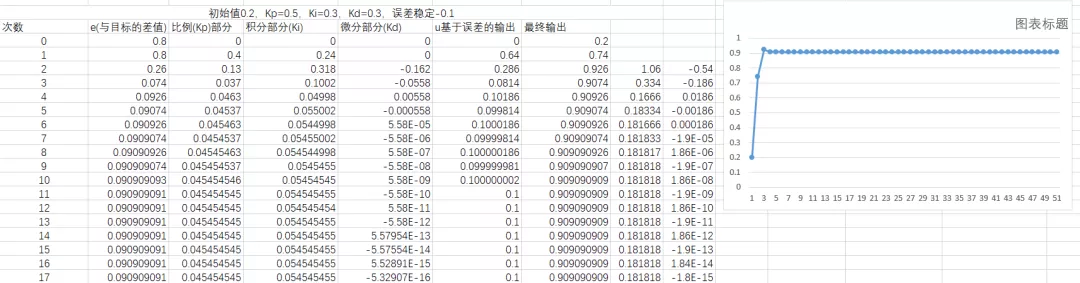
举例说明,当前小车速度为0.2,目标速度是1。输出y和输入x的关系是y=1*x。比例系数Kp=0.5。随着时间的增大,输出和输入关系如下。
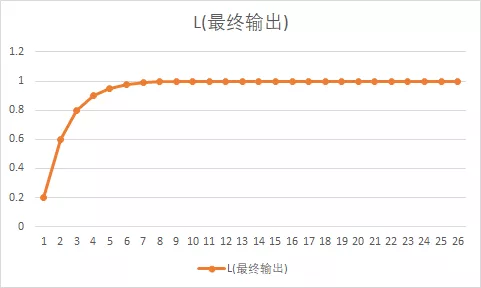
直观折线图显示如下:
我们发现这太完美了,那么比例环节就能够完美的解决问题了,可是等等,在下这个结论前,我们忽略一个特因素:噪声误差。
在很多系统中都是有噪声的,这我们举例小车中,噪声误差可能来自于电机的误差,外部因素风阻等误差,且是波动的。我们将问题简化,假设外部因素恒定,外部因素是的小车实际输出速度减去1。
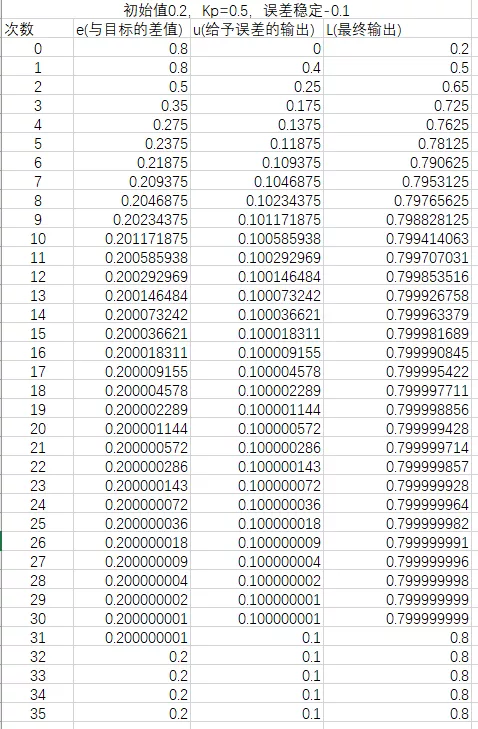
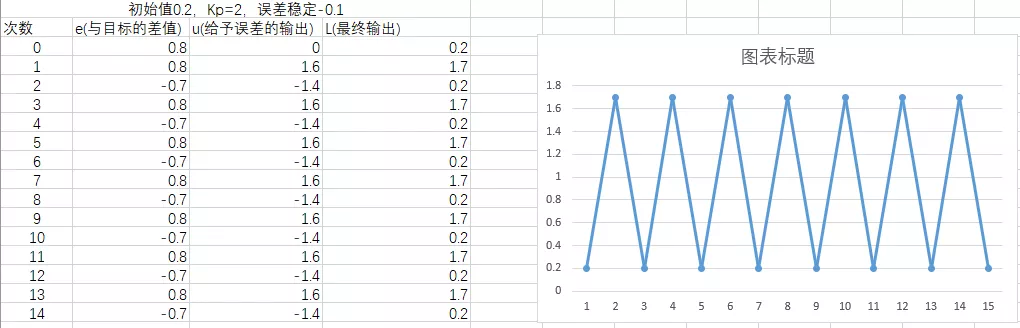
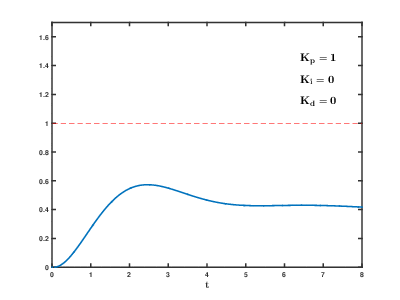
还是上面的例子,当前小车速度为0.2,目标速度是1。输出y和输入x的关系是y=1*x。比例系数Kp=0.5,恒定的误差为-0.1,随着时间的增大,输出和输入关系如下。
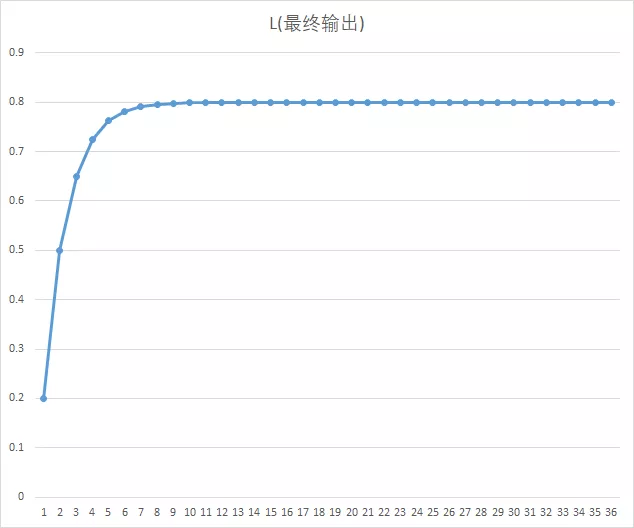
直观折线图显示如下:
最终输出稳定在0.8,因为我们初始值为0.2,到最后和目标差值是0.2,补偿是0.1,误差正好是-0.1,也就是说等于我们没有补偿。
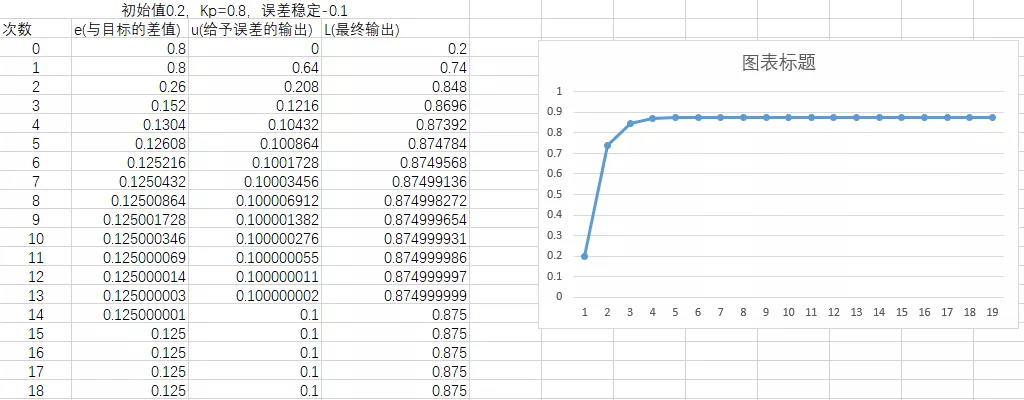
如果我们需要速度达到1呢???办法就是增大比例系数Kp。
误差为0.8时
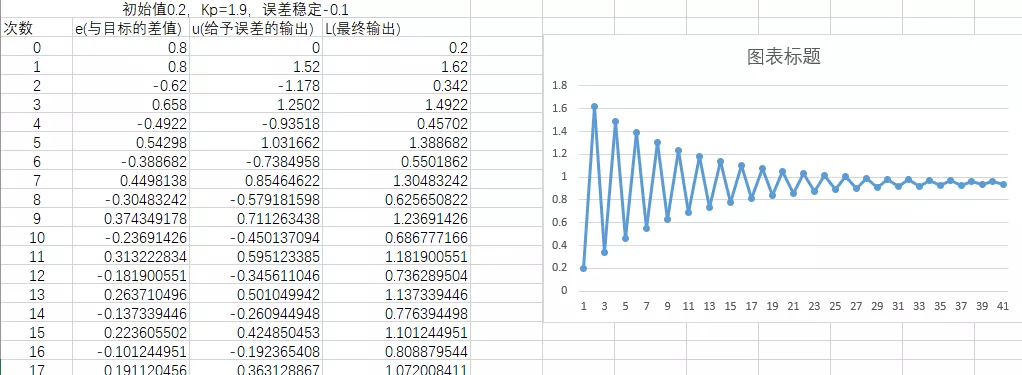
误差为1.9时
误差为2时,已经完全震荡
结论:比例控制引入了稳态误差,且无法消除。比例常数增大可以减小稳态误差,但如果太大则引起系统震荡,不稳定。
3、积分调节
为了消除稳态误差,第二次加入积分,使用PI(比例积分控制),积分控制就是将历史误差全部加起来乘以积分常数。公式如下:
u(t) -------------输出曲线,pid输出值随时间的变化曲线
Kp --------------比例系数
e(t)--------------偏差曲线,设定值与实际值的偏差随时间的变化曲线
t-----------------时间
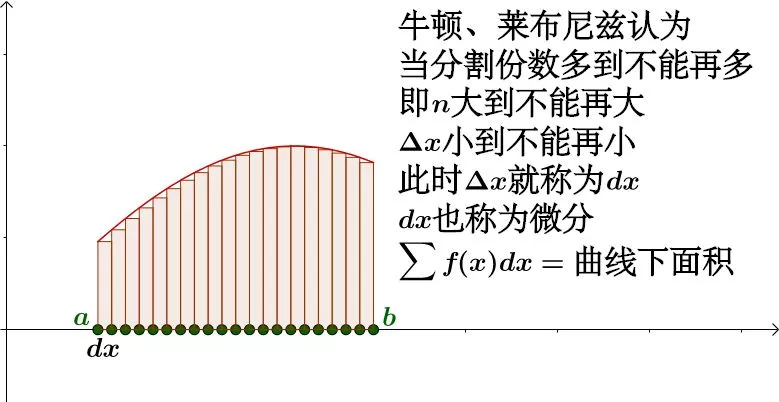
关于定积分,如果你上过高数,且没有睡觉的话。
需要将数学公式离散化,才能用到计算机系统来。
①表示在时间点t,输出的值
②表示在时间点t,输出的误差
③表示从时间0到t,累计误差。
添加Ki参数之后的折线图如下
结论:
只要存在偏差,积分就不停的累计,直到误差为0,积分项不再累加,变成一个常数,可以抵消稳态误差.
4、微分调节
引入积分可以消除稳态误差,但会增加超调,且Ki增大,超调量也增大.
为了消除超调,我们引入微分作用
积分就是e(t)曲线的斜率。
将公式离散化为
ek是当前误差,ek-1是上一次误差,所以①就是误差曲线的斜率。
关于PID公式还有其他写法,本质是一样的
离散化后是
u(t) -------------输出曲线,pid输出值随时间的变化曲线
Kp --------------比例系数
e(t)------------- 偏差曲线,设定值与实际值的偏差随时间的变化曲线
Ti--------------- 积分时间
Td--------------微分时间
T----------------调节周期
那么PID的参数如下
将前面的示例,加入微分项,Ki=0.3。
折线图如下
结论:微分能够减弱超调趋势。
5、总结
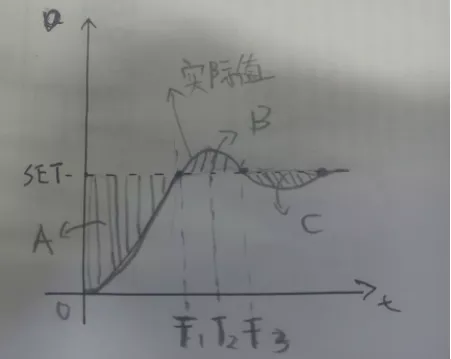
PID调节示意图如下:
可以发现:
比例项是纠正偏差的主力,越远离偏差绝对值就越大,快速把偏差纠正回来。
积分项和以往的状态有关,面积的绝对值越大它的绝对值就越大,它的作用是消除累计偏差。
微分项跟斜率有关,比较难解释,总的来说它的作用是:当目标靠近设定值时加速它靠近,当目标远离设定值时阻止它远离。因此微分可以增加系统稳定性,因为到达目的之后,离开会受到阻碍。
6、增量PID
上面我们讲解的是位置PID,还有一种增量PID,输出的不是目标值,而是与上次值的差值。直观上将就是u(t)-u(t-1)。
那么u(t)-u(t-1)的公式是
位置型PID控制器的基本特点:
- 位置型PID控制的输出与整个过去的状态有关,用到了偏差的累加值,容易产生累积偏差。
- 位置型PID适用于执行机构不带积分部件的对象。
- 位置型的输出直接对应对象的输出,对系统的影响比较大。
增量型PID控制器的基本特点:
- 增量型PID算法不需要做累加,控制量增量的确定仅与最近几次偏差值有关,计算偏差的影响较小。
- 增量型PID算法得出的是控制量的增量,对系统的影响相对较小。
- 采用增量型PID算法易于实现手动到自动的无扰动切换。
7、代码编程
位置PID
- /*******************************************************************
- 位置式pid
- ********************************************************************/
- double PID(double Actual,double SET)
- {
- static double E_sum,Error_last; //上一次误差
- double kp=20.767,ki=1.867,kd=115.55;
- double pid_out;
- double Error_now; //当前误差
- Error_now = SET-Actual; //当前误差
- // if(Error_now>-0.9&&Error_now<0.9) //防静态误差
- // {
- // Error_now=0;
- // Error_last=0;
- // }
- E_sum += Error_now; //误差累计
- // if(E_sum>484)E_sum=484; //积分限幅度,防止积分饱和
- // if(E_sum<-484)E_sum=-484;
- pid_out= kp * Error_now + ki * E_sum + kd * (Error_now-Error_last); //pid计算公式
- Error_last=Error_now;
- // if(pid>900) pid=900; //输出限幅
- // if(pid<-900)pid=-900;
- return -pid_out;
- }
增量PID
- error = target_speed - current_speed;
- P_error = error;
- I_error = error - left_motor.L_error;
- D_error = error - 2*left_motor.L_error + left_motor.LL_error;
- add = (s16)(KP * P_error + KI * I_error + KD * D_error);
- left_motor.ESC_output_PWM += add;
- left_motor.LL_error = left_motor.L_error;
- left_motor.L_error = error;
本文转载自微信公众号「知晓编程」,可以通过以下二维码关注。转载本文请联系知晓编程公众号。