寻找旋转数组中的最小数字-旋转数组的最小数字

[[409450]]

本文转载自微信公众号「神奇的程序员K」，作者神奇的程序员K。转载本文请联系神奇的程序员K公众号。

前言

把一个数组最开始的若干个元素搬到数组的末尾，就称之为数组的旋转。有一个递增排序数组，将其开头的若干个元素移动至数组的末尾，寻找其中的最小值。

本文就跟大家分享下如何用最快的速度找到递增旋转数组中的最小值，欢迎各位感兴趣的开发者阅读本文。

实现思路

乍一看这个问题，一部分开发者首先想到的解法就是从头到尾遍历下数组，这样就能找出最小的元素。这种思路的时间复杂度是O(n)，没有将题目中的条件利用起来，因此这种方案不是本题的正确答案。

举例分析

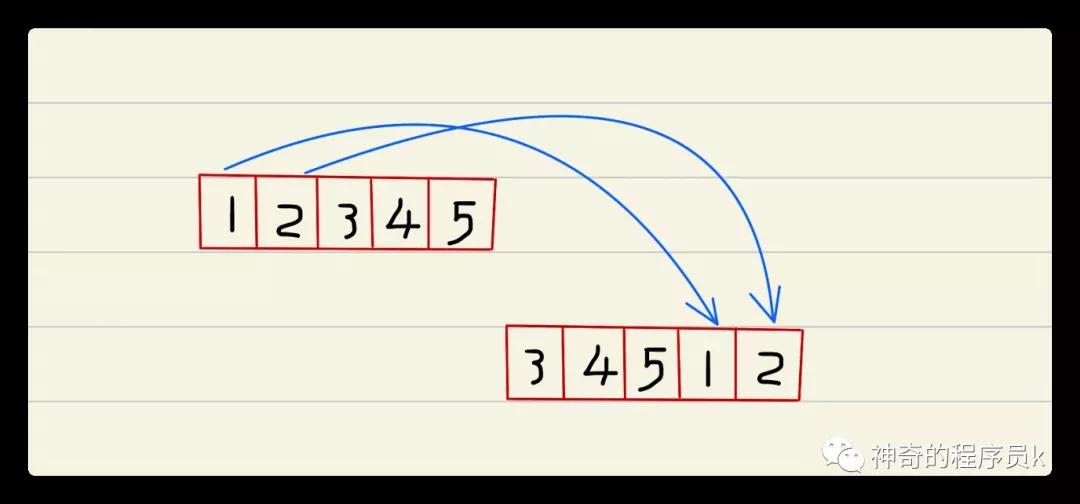
接下来，我们来分析下题目，通过举例、观察来寻找突破口。我们先来列举一个递增数组。

如上图所示，我们准备了一个1 ～ 5的递增数组，然后将其开头的两个元素搬到了数组的末尾，这样就构成了一个旋转数组。

经过一番观察后，我们可以发现：

旋转后的数组可以划分为两个已经排序的小数组
前面子数组的元素都大于等于后面子数组的元素
最小的数字是这两个子数组的分界线

二分查找

经过上面的分析，我们可知旋转后的数组在一定程度上是排好序的，因此我们可以尝试使用二分查找的思路来寻找最小的元素。

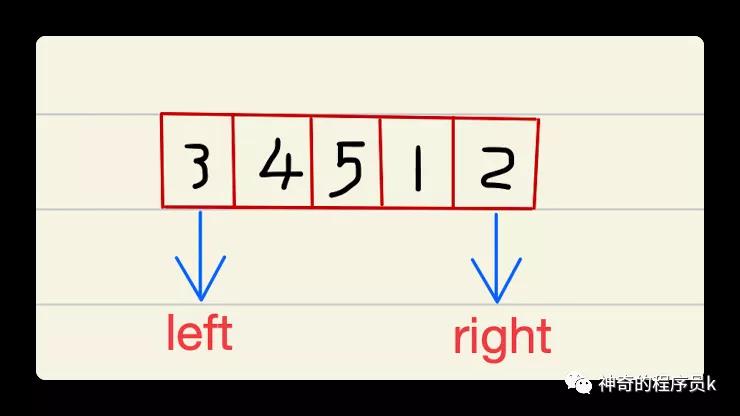
接下来，我们准备两个指针(左指针、右指针)，左指针指向数组的第一个元素，右指针指向数组的末尾元素，如下图所示：

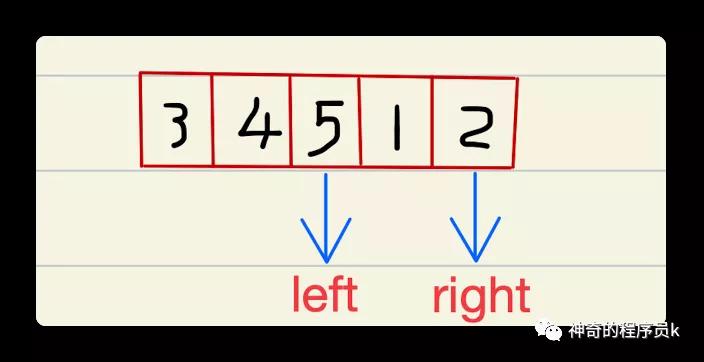
观察上图后，我们发现它们的中间元素是5、最小值在5的后面，因此我们就可以排除中间值之前的元素了，移动左指针至5，如下图所示：

此时，它们的中间元素是1，我们发现最小值2的前面，因此我们就可以将右指针移动至中间1，如下所所示：图片

最后，我们发现左指针与右指针相邻，右指针指向的元素正好是旋转数组的最小元素。

经过上述画图分析后，我们可以得到如下规律：

如果两个指针的中间元素大于等于左指针指向的元素，那么最小值一定在中间元素的后面，移动左指针至中间值位置缩小查找范围
如果两个指针的中间元素小于等于右指针指向的元素，那么最小值一定在中间元素的前面，移动右指针至中间值位置缩小查找范围
左指针一定指向前面的递增子数组，右指针一定指向后面的递增子数组
当左、右指针相邻时，右指针所指向的元素就是这个数组的最小值

时间复杂度分析：每次移动指针，查找范围都会缩小到原先的一半，因此总的时间复杂度为O(logn)

特殊情况

上述规律可以满足大多数情况，当出现下述情况时我们就不能采用二分查找了：

当数组的0号元素小于最后一个元素时，证明这个数组是排好序的，它的最小值是数组的第0号元素
当左指针与右指针指向的元素相同且它们的中间元素也与其相同，那么就只能使用顺序查找，如下图所示：

实现代码

接下来，我们根据上述所讲内容来总结下思路：

判断数组是否已经排好序(第一个元素是否小于最后一个元素)
左指针指向的值大于等于右指针指向的值就根据条件移动左、右指针：
- 循环终止条件：左指针与右指针相邻
- 求左、右指针的中间索引
- 左指针指向的值与右指针指向的值相同且中间元素也与之相同(使用顺序查找 )
- 中间值大于等于左指针指向的值，移动左指针位置至中间值位置
- 中间值小于等于右指针指向的值，移动右指针位置至中间值位置
循环结束，返回最小值

代码如下所示：

// 把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。 
// 输入一个递增排序的数组的一个旋转，输出旋转数组的最小元素。 
// 例如，数组[3，4，5，1，2]为[1，2，3，4，5]的一个旋转，该数组的最小值为1。 
 
export default class FindWhirlingArrayMinVal { 
  private leftPointer; 
  private rightPointer; 
  private middleIndex; 
 
  constructor() { 
    this.leftPointer = 0; 
    this.rightPointer = 0; 
    this.middleIndex = 0; 
  } 
 
  public getMinValue(incrementArray: Array<number>): number { 
    this.rightPointer = incrementArray.length - 1; 
    // 第一个元素小于最后一个元素，证明数组是排好序的 
    if (incrementArray[this.leftPointer] < incrementArray[this.rightPointer]) { 
      // 其最小值为第一个元素 
      return incrementArray[this.leftPointer]; 
    } 
    while ( 
      incrementArray[this.leftPointer] >= incrementArray[this.rightPointer] 
    ) { 
      // 循环终止条件: 右指针与左指针相邻，最小值为右指针所指向的值 
      if (this.rightPointer - this.leftPointer === 1) { 
        this.middleIndex = this.rightPointer; 
        break; 
      } 
      // 求中间值 
      this.middleIndex = Math.floor((this.leftPointer + this.rightPointer) / 2); 
      // 左指针指向的值与右指针指向的值相同且中间元素也与之相同 
      // 则无法使用二分查找，需要顺序查找 
      if ( 
        incrementArray[this.leftPointer] === 
          incrementArray[this.rightPointer] && 
        incrementArray[this.middleIndex] === incrementArray[this.leftPointer] 
      ) { 
        // 按顺序查找 
        let minValue = incrementArray[0]; 
        for (let i = 0; i < incrementArray.length; i++) { 
          if (incrementArray[i] < minValue) { 
            minValue = incrementArray[i]; 
          } 
        } 
        return minValue; 
      } 
 
      if ( 
        incrementArray[this.middleIndex] >= incrementArray[this.leftPointer] 
      ) { 
        // 中间值大于等于左指针指向的值 
        // 移动左指针至中间值位置 
        this.leftPointer = this.middleIndex; 
      } else if ( 
        incrementArray[this.middleIndex] <= incrementArray[this.rightPointer] 
      ) { 
        // 中间值小于等于右指针指向的值 
        // 移动右指针至中间值位置 
        this.rightPointer = this.middleIndex; 
      } 
    } 
    // 循环结束，返回最小值 
    return incrementArray[this.middleIndex]; 
  } 
}

完整代码请移步：findWhirlingArrayMinVal-test.ts