Python中的盆地跳跃(Basin Hopping)优化

 [[407724]]

 Python中文社区(ID:python-china)

盆地跳跃是一种全局优化算法。它是为解决化学物理学中的问题而开发的，尽管它是一种适用于具有多个最优条件的非线性目标函数的有效算法。

在本教程中，您将发现盆地跳跃全局优化算法。完成本教程后，您将知道：

•  盆地跳跃优化是一种全局优化，它使用随机扰动来跳跃盆地，并使用局部搜索算法来优化每个盆地。
•  如何在python中使用盆地跳跃优化算法API。
•  使用流域跳跃来解决具有多个最优解的全局优化问题的示例。

教程概述

本教程分为三个部分：他们是：

•  盆地跳跃优化
•  盆地跳跃API
•  盆地跳跃的例子 局部最优的多峰优化 具有多个全局最优的多峰优化

盆地跳跃优化

Basin Hopping是为化学物理领域开发的一种全局优化算法。局部优化是指旨在为单变量目标函数定位最优值或在认为存在最优值的区域中运行的优化算法。而全局优化算法旨在将单个全局最优定位在潜在的多个局部（非全局）最优之中。David Wales和Jonathan Doye在1997年的论文中描述了“盆地跳跃”，题目是“通过盆地跳跃进行的全局优化和包含110个原子的Lennard-Jones团簇的最低能级结构”。

该算法包括循环两个步骤，一个是好的候选解的扰动，另一个是将本地搜索应用于被扰动的解。

扰动允许搜索算法跳到搜索空间的新区域，并可能找到导致不同最优值的新盆地，例如技术名称中的“跳槽”。局部搜索使算法可以遍历新盆地达到最佳状态。新的最优值可以作为新的随机扰动的基础，否则将被丢弃。保留新解决方案的决策是由具有“温度”变量的随机决策函数控制的，这与模拟退火非常相似。温度根据算法的迭代次数进行调整。这样可以在高温时在运行的早期就接受任意解决方案，而更严格的策略是在低温时在搜索的后期仅接受质量更好的解决方案。这样，该算法非常类似于具有不同（扰动）起始点的迭代局部搜索。该算法运行指定的迭代次数或函数求值，并且可以多次运行以提高对找到全局最优值或找到相对好的解决方案的信心。

现在，我们已经从较高的层次熟悉了基本的跳变算法，下面让我们看一下Python中用于盆地跳变的API。

盆地跳跃API

在Python中，可以通过Basinhopping（）SciPy函数来进行盆地跳跃。   

# perform the basin hopping search  
result = basinhopping(objective, pt)  

另一个重要的超参数是通过“ niter”参数运行搜索集的迭代次数，默认为100。可以将其设置为数千次迭代或更多次迭代。 

# perform the basin hopping search  
result = basinhopping(objective, pt, niter=10000) 

可以通过“步长”控制应用于候选解的扰动量，该“步长”定义了在问题域的边界范围内施加的最大变化量。默认情况下，将其设置为0.5，但应在域中将其设置为合理的值，以允许搜索找到新的盆地。例如，如果搜索空间的合理范围是-100到100，则步长为5.0或10.0个单位可能是合适的（例如，域的2.5％或5％）。 

# perform the basin hopping search  
result = basinhopping(objective, pt, stepsize=10.0) 

默认情况下，使用的本地搜索算法是“ L-BFGS-B”算法。可以通过将“ minimizer_kwargs”参数设置为关键字为“ method”且值作为要使用的本地搜索算法的名称（例如“ nelder-mead”）的目录来更改此设置。可以使用SciPy库提供的任何本地搜索算法。 

# perform the basin hopping search  
result = basinhopping(objective, pt, minimizer_kwargs={'method':'nelder-mead'})  

搜索的结果是一个OptimizeResult对象，可以在其中像字典一样访问属性。可以通过“成功”或“消息”键来访问搜索的成功与否。

可以通过“ nfev”访问功能评估的总数，并且可以通过“ x”键访问为搜索找到的最佳输入。

现在，我们已经熟悉了Python中的盆地跳跃API，下面我们来看一些可行的示例。

盆地跳跃的例子

在本节中，我们将研究在多模态目标函数上使用盆地跳跃算法的一些示例。多峰目标函数是具有多个最优值的函数，例如全局最优值和许多局部最优值，或者具有相同目标函数输出的多个全局最优值。我们将在这两个函数上查看流域跳跃的示例。

局部最优的多峰优化

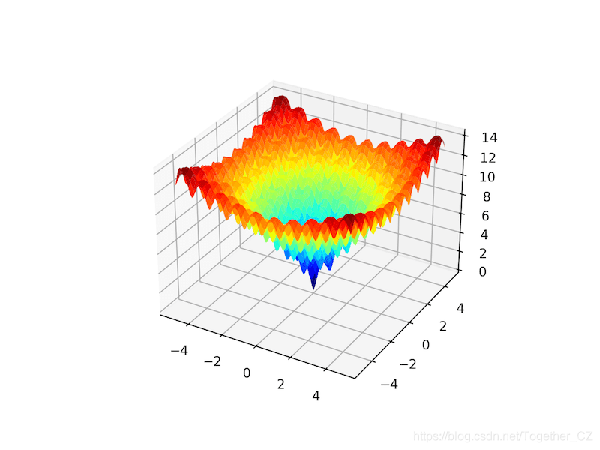
Ackley函数是目标函数的一个示例，该目标函数具有单个全局最优值和多个局部最优值，可能会在其中陷入局部搜索。因此，需要全局优化技术。这是一个二维目标函数，其全局最佳值为[0,0]，其值为0.0。下面的示例实现了Ackley，并创建了一个三维表面图，显示了全局最优值和多个局部最优值。 

# ackley multimodal function  
  from numpy import arange  
  from numpy import exp  
  from numpy import sqrt  
  from numpy import cos  
  from numpy import e  
  from numpy import pi  
  from numpy import meshgrid  
  from matplotlib import pyplot  
  from mpl_toolkits.mplot3d import Axes3D  
  # objective function  
  def objective(x, y):  
      return -20.0 * exp(-0.2 * sqrt(0.5 * (x**2 + y**2))) - exp(0.5 * (cos(2 * pi * x) + cos(2 * pi * y))) + e + 20  
  # define range for input  
  r_min, r_max = -5.0, 5.0  
  # sample input range uniformly at 0.1 increments  
  xaxis = arange(r_min, r_max, 0.1)  
  yaxis = arange(r_min, r_max, 0.1)  
  # create a mesh from the axis  
  x, y = meshgrid(xaxis, yaxis)  
  # compute targets  
  results = objective(x, y)  
  # create a surface plot with the jet color scheme  
  figure = pyplot.figure()  
  axis = figure.gca(projection='3d')  
  axis.plot_surface(x, y, results, cmap='jet')  
  # show the plot  
  pyplot.show() 

运行示例将创建Ackley函数的表面图，以显示大量的局部最优值。

我们可以将盆地跳跃算法应用于Ackley目标函数。

在这种情况下，我们将使用从-5到5之间的输入域绘制的随机点开始搜索。 

# define the starting point as a random sample from the domain  
pt = r_min + rand(2) * (r_max - r_min) 

我们将使用0.5的步长，200次迭代和默认的本地搜索算法。经过一番尝试和错误后，才选择此配置。 

# perform the basin hopping search  
result = basinhopping(objective, pt, stepsize=0.5, niter=200) 

搜索完成后，它将报告搜索状态，执行的迭代次数以及通过评估发现的最佳结果。 

# summarize the result  
 print('Status : %s' % result['message'])  
 print('Total Evaluations: %d' % result['nfev'])  
 # evaluate solution  
 solution = result['x']  
 evaluation = objective(solution)  
 print('Solution: f(%s) = %.5f' % (solution, evaluation)) 

结合在一起，下面列出了将盆地跳跃应用于Ackley目标函数的完整示例。   

# basin hopping global optimization for the ackley multimodal objective function  
   from scipy.optimize import basinhopping  
   from numpy.random import rand  
   from numpy import exp  
   from numpy import sqrt  
   from numpy import cos  
   from numpy import e  
   from numpy import pi  
   # objective function  
   def objective(v):  
       x, y = v 
       return -20.0 * exp(-0.2 * sqrt(0.5 * (x**2 + y**2))) - exp(0.5 * (cos(2 * pi * x) + cos(2 * pi * y))) + e + 20  
   # define range for input  
   r_min, r_max = -5.0, 5.0  
   # define the starting point as a random sample from the domain  
   pt = r_min + rand(2) * (r_max - r_min)  
   # perform the basin hopping search  
   result = basinhopping(objective, pt, stepsize=0.5, niter=200) 
   # summarize the result  
   print('Status : %s' % result['message'])  
   print('Total Evaluations: %d' % result['nfev'])  
   # evaluate solution  
   solution = result['x']  
   evaluation = objective(solution)  
   print('Solution: f(%s) = %.5f' % (solution, evaluation)) 

运行示例将执行优化，然后报告结果。

注意：由于算法或评估程序的随机性，或者数值精度的不同，您的结果可能会有所不同。考虑运行该示例几次并比较平均结果。

在这种情况下，我们可以看到该算法将最优值定位为非常接近零的输入，并且目标函数的评估值实际上为零。我们可以看到，该算法的200次迭代产生了86,020个函数求值。 

Status: ['requested number of basinhopping iterations completed successfully']  
 Total Evaluations: 86020  
 Solution: f([ 5.29778873e-10 -2.29022817e-10]) = 0.00000 

具有多个全局最优的多峰优化

Himmelblau函数是具有多个全局最优值的目标函数的示例。

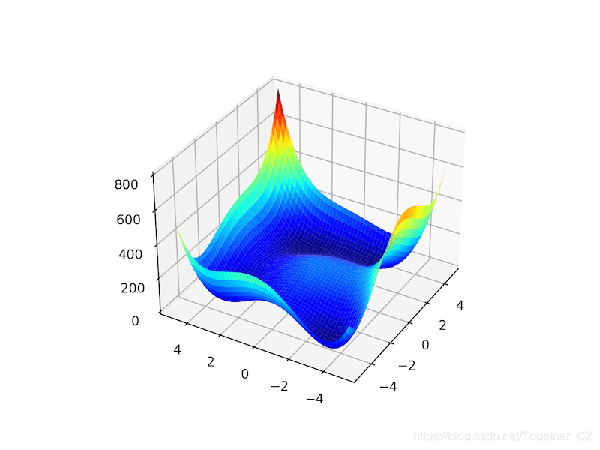
具体来说，它具有四个最优值，并且每个都有相同的目标函数评估。这是一个二维目标函数，其全局最佳值分别为[3.0，2.0]，[-2.805118、3.113112]，[-3.779310，-3.283186]，[3.584428，-1.848126]。这意味着全局优化算法的每次运行都可能找到不同的全局最优值。下面的示例实现了Himmelblau并创建了一个三维表面图，以直观地说明目标函数。 

# himmelblau multimodal test function  
from numpy import arange  
from numpy import meshgrid  
from matplotlib import pyplot  
from mpl_toolkits.mplot3d import Axes3D  
# objective function  
def objective(x, y):  
    return (x**2 + y - 11)**2 + (x + y**2 -7)**2  
# define range for input  
r_min, r_max = -5.0, 5.0  
# sample input range uniformly at 0.1 increments  
xaxis = arange(r_min, r_max, 0.1)  
yaxis = arange(r_min, r_max, 0.1)  
# create a mesh from the axis  
x, y = meshgrid(xaxis, yaxis)  
# compute targets  
results = objective(x, y)  
# create a surface plot with the jet color scheme  
figure = pyplot.figure()  
axis = figure.gca(projection='3d')  
axis.plot_surface(x, y, results, cmap='jet')  
# show the plot  
pyplot.show() 

运行示例将创建Himmelblau函数的表面图，该图将四个全局最优值显示为深蓝色盆地。

我们可以将盆地跳跃算法应用于Himmelblau目标函数。

与前面的示例一样，我们将使用从-5到5之间的输入域绘制的随机点开始搜索。

我们将使用0.5的步长，200次迭代和默认的本地搜索算法。搜索结束时，我们将报告最佳位置的最佳输入。 

# basin hopping global optimization for the himmelblau multimodal objective function  
  from scipy.optimize import basinhopping  
  from numpy.random import rand  
  # objective function  
  def objective(v):  
      x, y = v  
      return (x**2 + y - 11)**2 + (x + y**2 -7)**2  
  # define range for input  
  r_min, r_max = -5.0, 5.0  
  # define the starting point as a random sample from the domain  
  pt = r_min + rand(2) * (r_max - r_min)  
  # perform the basin hopping search  
  result = basinhopping(objective, pt, stepsize=0.5, niter=200)  
  # summarize the result  
  print('Status : %s' % result['message'])  
  print('Total Evaluations: %d' % result['nfev'])  
  # evaluate solution  
  solution = result['x']  
  evaluation = objective(solution)  
  print('Solution: f(%s) = %.5f' % (solution, evaluation)) 

运行示例将执行优化，然后报告结果。

在这种情况下，我们可以看到该算法在[3.0，2.0]处确定了一个最佳值。

我们可以看到，该算法的200次迭代产生了7,660个函数评估。 

Status : ['requested number of basinhopping iterations completed successfully']  
 Total Evaluations: 7660  
 Solution: f([3. 1.99999999]) = 0.00000 

如果我们再次运行搜索，则可能期望找到其他全局最优值。

例如，下面，我们可以看到一个最佳值位于[-2.805118，3.131312]处，与之前的运行不同。 

Status : ['requested number of basinhopping iterations completed successfully']  
Total Evaluations: 7636  
Solution: f([-2.80511809 3.13131252]) = 0.00000