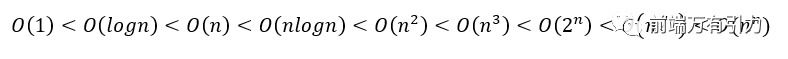写在前面
大厂秋招提前批已经开启，吹响了应届生秋招的号角，也就意味着大家要加入残酷的招聘竞争。笔试面试是规范求职过去的坎，而算法对于大多数人而言是是道难关，只有通过系统学习和理解刷题才能征服它。
为了帮助更多人去理解数据结构和算法，将开辟新的博文系列《懂点算法》，希望大家能够渡过痛苦的日子。本人在算法研究上，能力有限，希望大家能够取其精华，汲取干货。
什么是算法
算法(Algorithm)是指用来操作数据、解决程序问题的一组方法。
衡量不同算法之间的优劣有两种方法：
- 事后统计法：通过统计、监控，利用计算机计时器对不同算法的运行时间进行比较，从而确定算法效率的高低，但是具有非常大的局限性。
- 事前分析估算法：在计算机程序编制前，依据统计方法对算法进行估算。
举个栗子，我们知道斐波那契数列的规律是：数列从第3项开始，每一项数值是前两项数值之和。即：0,1,1,2,3,5,8...
分析：我们观察斐波那契数列的规律，可以看到数列在使用算法进行表示的时候，需要分为两种情况，即前两项，和第三项开始后的元素的计算。
最简单的方法是使用递归进行实现斐波那契数列的算法：
- function fib(num){
- if(num <= 1) return num;
- return fib(num - 1) + fib(num - 2);
- }
当然，也可以使用循环方法进行实现：
- function fib(num){
- if(num <= 1) return num;
- let num1 = 0, num2 = 1;
- for(let i = 0; i < num - 1; i++){
- // 每次加都是前两项之和
- let sum = num1 + num2;
- // 相加之前num2要作为下一次相加的num1
- num1 = num2;
- // 相加的结果要作为下一个num2
- num2 = sum;
- // 但是呢，上面两句代码不可交换哦
- }
- return num2;
- }
其实，高级程序语言编写的程序在计算机上运行的消耗时间取决于以下因素：
- 算法采用的策略、方法(算法的好坏)
- 编译产生的代码质量(软件性能)
- 问题的输入规模(输入量的多少)
- 机器执行指令的速度(硬件性能)
总的来说，程序的运行时间主要取决于算法的好坏和问题的输入规模。
时间复杂度和空间复杂度
我们都学过高斯的故事，主要内容是这样的：在高斯上学时老师提问如何计算100以内非0自然数的和，即计算1+2+……+99+100=? 当时很多同学都在从头加到尾计算，但是高斯并没有忙着去计算，而是思考问题。
经过高斯观察后发现，第一项与最后一项的和等于第二项与倒数第二项的和一样，都是101，同时他发现其他项也符合这样的规律。而总共有50对，所以结果就是101×50=5050。于是，他成为班里第一个计算出答案的人。
告诉我们道理：磨刀不误砍柴工，用对方法更轻松。
那么，我们仔细分析下高斯算法和常规算法的优劣。
常规算法：
- function commonFunc(){
- let sum = 0; //执行一次
- for(let i = 1; i <= 100; i++){ //执行n+1次
- sum += i;//执行n次
- }
- return sum;//执行1次
- }
高斯算法：
- function guassFunc(){
- let sum = 0;//执行1次
- sum = (1 * ｎ) ＊ ｎ／２；//执行1次
- return sum;//执行1次
- }
如上所示，常规算法的执行次数是2n+3次，而高斯算法的执行次数是3次。由于首尾语句的执行次数是相同，主要关注中间算法部分则是n次与1次的区别，很显然高斯算法远优于常规算法。
算法时间复杂度
我们看下《大话数据结构》中是如何定义算法时间复杂度的。
算法时间复杂度：在进行算法分析时，语句总的执行次数T(n)是关于问题规模n的函数，进而分析得到T(n)随n的变化情况并确定T(n)的数量级。算法的时间复杂度，就是算法的时间量度，记作：T(n)=O(f(n))。它表示随时间规模n的增大，算法执行时间的增长率和f(n)的增长率相同，称作算法的渐进时间复杂度，简称时间复杂度。
我给你翻译翻译，就是说时间复杂度是用于估算程序运行时间的量度。假设算法的问题规模为n，那么操作单元数量(用于表示程序消耗的时间)，随着数据规模n的增大，算法执行时间的增长率和f(n)的增长率相同，称作时间复杂度O(f(n))。
T(n)=O(f(n))
- T(n)表示代码执行的时间
- n表示数据规模的大小
- f(n)表示每行代码执行的次数总和
- O表示代码执行时间T(n)与T(n)成正比
我们看到上面描述中提到了O()来体现算法时间复杂度，也被称为大O计法。大O用于表示上界，即用于表示算法最坏情况下运行时间的上界，也就是在最坏情况下运行所花费的时间。
推导大O阶方法：
- 用常数1取代运行时间中的所有加法常数
- 在修改后的运行函数次数中，只保留最高阶项
- 如果最高阶项存在且不是1，则去除与这个项相乘的常数
接着，我们自己动手练习下算法时间复杂度的计算方法，如下：
- function testFunc(n){
- for(let i = 0; i < n; i += i){ //执行1+log2(n)次
- for(let j = 0; j < n; j++){ //执行n+1次
- console.log("yichuan");//执行(1+log2(n))*(n+1)次
- }
- }
- }
我们看到，在第一次for循环中，i+=i即i=i+i=2i，那么当2i=n时得到n=log2(n)，要跳出循环即要执行1+log2(n)次语句。而在第二次for循环中语句要执行n+1次才能跳出循环，而打印语句的执行次数是(1+log2(n))*(n+1)次。其实采用大O记数法忽略加法常数和最高次项系数，那么得到就是执行nlogn次，记作O(nlogn)。
记住，在计算算法时间复杂度时，可以根据高阶次数的实际情况忽略其加法常数和最高次项系数、对数项的底数。
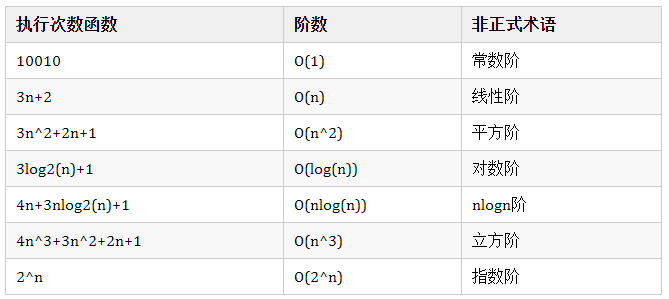
常见的计数阶数有：
我们可以看到常见的算法时间复杂度计算阶数所耗费时间的比较：
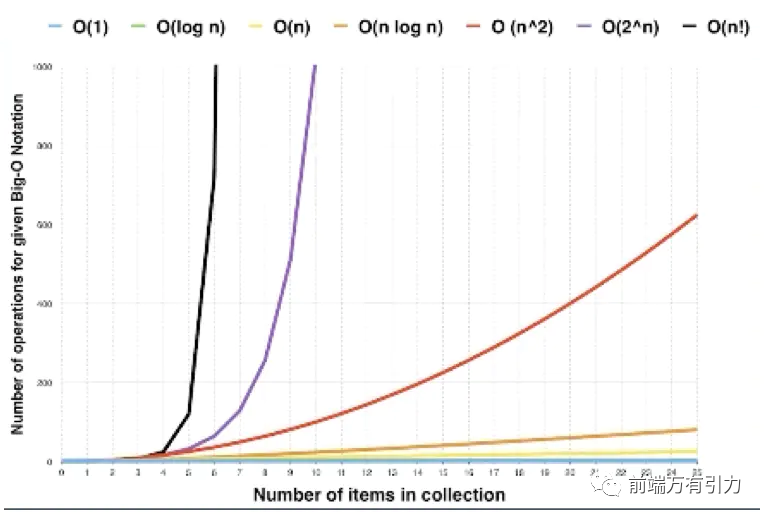
各种时间复杂度曲线如下：
算法空间复杂度
其实，在代码时完全是牺牲空间来换取时间。类比于算法时间复杂度，空间复杂度表示算法存储空间与数据规模之间的增长关系。
算法空间复杂度：通过计算算法所需的存储空间实现，而计算公式是：S(n)=O(f(n))。
- n表示问题的规模
- f(n)表示语句中关于n所占存储空间的函数
- function spaceFunc(n){
- const arr = [];//第2行代码
- arr.length = n;//第3行代码
- for(let i = 0; i < n; i++){
- arr[i] = i * i;
- }
- for(let j = n - 1; j >= 0; --j){
- console.log(arr[i]);
- }
- }
观察上述代码可得：在第2行代码中，在内存开辟一块空间存储变量arr并对其赋值空数组;在第3行代码中，将数组的长度设置为n，数组中会自动填充n个undefined;此外剩下代码并未占据更多空间，因此整段代码的空间复杂度为O(n)。
最坏情况和平均情况
最坏情况运行时间是这段程序在运行所耗费时间最多的情况，没有比这更糟糕的情况。通常，我们提到的运行时间指的都是最坏情况的运行时间。
平均情况运行时间所指的是程序所期望的平均时间，但是在实际测试中，很难通过分析得到，需要通过一定数量的实验数据和估算。
我们知道，在进行查找n个随机数中查找某个数字，最好的情况是查找第1个数字就找到，此时的时间复杂度是O(1)，而最坏的情况下是查找到第n个数字才找到。那么，在查找数字的算法中最坏情况的时间复杂度是O(n)，平均情况的时间复杂度是O((1+n)/2)即O(n/2)。
小结
在本文中，笔者介绍了什么是算法、为什么要用算法、如何衡量算法的时间复杂度和空间复杂度以及算法的最坏情况和平均情况的概念。
