前言
近来,增大模型规模成为了提升模型性能的主要手段。特别是NLP领域的自监督预训练语言模型,规模越来越大,从GPT3的1750亿参数,到Switch Transformer的16000亿参数,又是一个数量级的增加。
模型规模的数量级的增大,虽然取得了一定程度的性能提升,甚至产生了某些意想不到的“神奇”效果(如GPT3),但其背后的计算开销成了最大的问题,比如GPT3训练使用了万级的GPU和数周的训练时间。如何既能利用超大规模的参数来提升模型表达和性能,又能控制计算量的较小的增加,成为了最主要的挑战之一。以MoE为代表的动态神经网络技术被重点引入。大脑是典型的低能耗高效率的计算模式,稀疏激活是最重要的特性。除了巨型模型在训练推理特别是训练时的计算效能挑战外,当前巨型模型的训练优化算法另一个更大的挑战是(不在此处讨论),BP算法是当前最为可用的深度网络优化,但更理想的优化算法需要高并行、优化过程非对称、并能够在时空维度通过局部持续优化完成整体优化。
1. 传统的神经网络模型,前馈的时候,输入的batch中,每一个样本的处理,都将激活网络中的每一个参数参与计算。
2. 条件计算最宽松的定义,指仅激活网络中某些部分的一类算法。Conditional Computation refers to a class of algorithms that activate only some of the different parts in a network. 在具体某类条件计算实现中,条件选择模式,可能按照输入的batch中每sample独立激活网络不同部分,可能按照输入数据空间上不同的部分(比如image不同区域或者channel),可能按照输入数据时间上不同的部分(比如time series的不同slide window或者video的不同的frame。),可能按照目标任务的不同每task独立的,可能按照非可学习的固定的随机分配不同的子网独立计算。
3. 对不同的输入(原始或者前层),按照一定条件,选择性的执行后续部分网络的计算,这个技术下,有一些近似或相关的技术,如:dynamic neural network(s), conditional computing, conditional activation, sparse activating, selective execution, mixture of experts (MoE), dynamic routing, …;强相关的一些模型比如 Switch Transformer等。
条件计算的分类(广义)
1. 按照routing是否可学习可以分为:learnable routing conditional computation和 unlearnable routing conditional computation.
2. 按照activation是否不执行non-activation计算,可以分为:hard conditional computation和soft conditional computation。对于hard-mode的条件计算,通过tensor挑选切分等操作,无论何种条件选择模式,不需要激活的数据将完全不参与不激活的网络部分的计算;soft-mode的条件计算,可能仅采取将相关数据置零等方式来避免产生计算效果,但还是和不需要激活网路部分实际执行计算过程。
条件计算的主要优势
1. 计算有效,降低能耗:通过部分激活部分计算,以每样本条件激活的条件计算为例,单个样本只需要经过整个SuperNet的一部分参与计算。
2. 更大网络,表达更强:由于一处到多处的Route,各处(层)的Input被路由到不同的子网独立计算,不同的输入的相互在各层的表达相对独立没有影响,表达能力更强,网络可以更大,但表达效率降低了。
条件计算的网络和计算形式
条件计算的网络和计算形式比较灵活,部分构建形式如:(此处省略具体模型和论文引用,参见: http:// intellabs.github.io/dis )
1. 按照CV等task的特点,用多个独立的CNN作为expert网络,按照task来独立路由,尾部组合后给一个大网络。
2. 使用更复杂的cascading等形式组合不同层级的不同的expert网络。
3. 通过决策树等方法做数据变换实现路由。
4. 通过可学习的网络来选择路由。其中策略学习的损失有多种构建形式:直接使用分类等任务的主损失,对不同专家的重要性和负载构建损失作为辅助损失等等。
条件计算的路由策略
1. non-learnable/hard-mode,通过某种确定性策略,如LSH等方式计算路由。
2. learnable-mode,通过可学习网络计算路由。网络规模可大可小,简单的可学习路由为单层权重:G(x) = P(X*W),G(x)为路由Gate函数,X为输入, W为通损失函数来度量的可学习路由权重,P为某种挑选函数(如topk, sort等),在实际实现中,X*W的输入与权重计算结果可能作为后续网络的输入信息的一部分,不仅仅利用G(x)来选择路由,则需要对X*W的结果做归一化,更典型的形式则为:G(x)=P(N(X*W)),其中N为表达Normalization函数,如Softmax。
条件计算的冗余策略
条件计算的冗余策略,可分为无冗余条件计算和冗余条件计算:
1. 无冗余条件计算可通过P(.)函数的实现如topk(k=1,…)来实现;
2. 冗余条件计算,可以多种实现形式,可以通过P(.)函数的实现如topk(k=n,…),n>=2来实现,也可以通过硬冗余模式,整个网络中支持输入的复制和多路计算实现。
条件计算的挑战
1. 路由算法对模型质量的影响无论输入和路由权重作用的信息(X*W),是仅作为路由选择并作为后续网络单元的输入,还是直接作为后续网络单元的输入的一部分,路由算法决定了输入信息的处理流向,对模型的整体质量都有很大影响。2. 路由(routing)/门(gate)的稳定性随机初始化的路由/门的权重,权重自身在不断被训练调整;在前后层的网络持续训练变化,同一样本在训练的不同阶段会被分派到不同的后续网络单元中,这种动态变化过于剧烈,将严重影响整个网络训练过程的稳定性和收敛速度。3、路由的专家样本重要性和负载的平衡性
训练阶段,每专家和样本批次中样本的关联度重要性,和每批次中样本被均衡分派到不同专家的负载平衡性,这两个指标既相关又冲突。需要分别构建损失函数作为辅助损失,来优化这两个指标。在arxiv:1701.06538《Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer》做了相关讨论。
关于条件计算/动态神经网络
关于条件计算/动态神经网络,更多的信息在《Dynamic Neural Networks: A Survey》arxiv:2102.04906 ( http:// arxiv.org/abs/2102.0490 )一文中,作者对广义的动态神经网络,将各种动态网络相关的技术按照实例级、时间级、空间级做了分类。
- 1. Instance-wise Dynamic NN:逐实例动态,每样本独立激活不同的网络和参数(MoE为这个方向)。Dynamic Architecture:Dynamic Depth、Dynamic Width、Dynamic Routing/MoE;Dynamic Parameter:Parameter Adjustment、Parameter Prediction、Dynamic Feature(s)
- 2. Spatial-wise Dynamic NN:空间级动态:图像等不同空间位置激活后续不同网络和参数。(CNN等):Pixel Level、Region Level、Resolution Level
- 3. Temporal-wise Dynamic NN:时间级动态:时序数据按时序维切分激活后续不同网络和参数。(video-frames, text-sequence, time-series, stream, ...)Text-SequenceVideo-Frames
上述为该综述论文对Dynamic NN的总体分类。
从超大规模网络动态网络技术支撑角度,高表达能力,低计算代价为主的来考虑分类,从两个维度对动态网络技术分类:
1. 按照在前馈计算时是否部分激活:
Hard-Dynamic:在前馈的时候,部分网络绝对不激活参与计算
Soft-Dynamic:在前馈的时候,部分网络经过softmax等gate/route后,通过张量元素置零等方式,失去表达能力,但会参与计算。
2. 按照动态激活判定算法的输入:
- 逐样本级:(在输入层)按照每样本的实例来决定动态网络的后续激活。
- 亚样本级:(在输入层)样本内时间/空间级激活不同的后续网络单元。一般深度网络,不仅在输入层会被选择性激活执行,在中间层也类似。
其中,智能平台支持Hard-Dynamic逐样本级的动态神经网络,能比较自然的获得网络结构大颗粒的稀疏激活,在超大模型中能实现训练和推理的高能效。
动态神经网络相比与静态结构的神经网络,在相关研究中,从效能,表达,泛化、鲁棒,可解释等方面做了大量对比研究。从智能平台通过计算成本尽量低的支持超大规模网络来提升模型性能的角度看,Efficiency和Representation最为重要:
1、Efficiency:静态网络“牵一发而动全身”,每一个样本输入整个网络/所有参数都要响应,这对超大网络来取得领先效果的模型能耗挑战太大。
2、Representation: 参数量更大,表达容量更大;但MoE等结构在深度网络的各层特征的表达上,复用降低,每参数的表达效率更低。
实现策略
实现各种模型的带有动态路由稀疏激活的超大规模参数版本,需要分模型研究和实现。
以Switch Transformer为例,其参数扩展到部分在Transformer的FFN部分。其MoE化扩展,如下图:
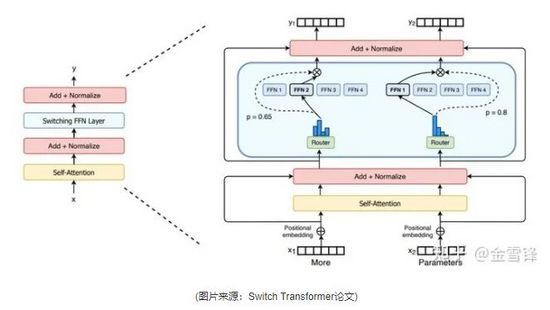
(图片来源:Switch Transformer论文)
可见,MoE化主要变化在需要Expert子网络前后增加MoE相关的逻辑。本文主要介绍平台上的实现。动态路由条件计算,主要包括四个步骤:路由计算、数据分派、独立计算,结果合并。
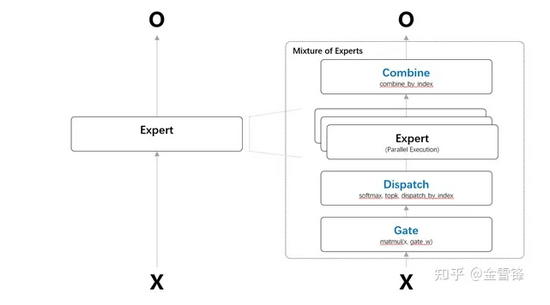
1. 路由计算-Gate:根据输入(可以为整个网络的输入,或者前面网络单元/层的输出),在路由单元完成计算,在以batch内sample-wise的路由中,计算出每个样本要分派的后续网络路由(Mixture-of-Experts/MoE中的专家)。
2. 数据分派-Dispatch:从输入的整体的Tensor中,按照路由计算的样本-专家关系,收集合并出每个专家需要处理的Tensor。如果在固定expert-batch的设计中,要平衡每批训练中,分派到每个专家的样本数和专家每轮训练最大容量,由于样本输入的随机性,很难保证较为均匀的分派,对于低于最大容量的批次,对固定batch-size的要做pad,对于高于最大容量的样本,可以采用延后重采样等方式。为了维护正确的输入输出关系(Input/X – Label/Y)和训练是反向传播的求导关系,实现中需要维护原始batch到每专家的sub-batch的index关系,在后来求导和结合合并时使用。
3. 独立计算-Expert:并发(逻辑上可以先后)调用各个专家处理对应的sub-batch。这也是智能平台要支持的并发API之一。
4. 结果合并-Combine:合并每专家的结果tensor到整个batch的tensor,并按照数据分派索引,交换到原始输入的顺序。
在主流的深度学习智能平台中,可以采用两类主要的实现策略:
张量置零:对需要分派到不同的后续网络单元(专家网络子网等),对需要分派的专家拷贝若干份tensor,对于不应输入当前专家处理的数据维度置零。该方式在保证置零计算逻辑正确的情况下,实现简单,全张量操作,对平台无特殊要求,适用于算法研究,仅体现条件计算前序数据被动态路由到不同的后续网络单元,分析算法的效果。如果通过置零方式,该方法每个专家处理的tensor在batch维度大小是全batch,不能节省计算量和内存使用量。
张量整理:对需要分派到不同的后续网络单元(专家网络子网等),对需要分派的专家拷贝若干份tensor,对于不应输入当前专家处理的数据维度不保留。并维护好sample级的index在变换前后的对应关系。在分布式友好的实现中,如果专家子网为单位被划分到不同的计算节点,那么专家网络的实现最好从子网级的平台对象继承后实现,比如:MindSpore中的mindspore.nn.Cell。详细实现细节参见后续技术实现章节。
核心代码
核心代码:路由计算、数据分派、独立计算,结果合并
参考代码采用MindSpore示意实现。(注:import mindspore as ms)
Mixture of Experts的核心逻辑,对输入I,经过routing_network(最简单*W即可),然后topk(若变种算法需要gate权重则需要softmax,否则可不),然后用tensor的操作(可按照batch)选择出每个subnetwork/expert的张量。
为方便调试,采用了规模极小的非随机的确定数值构造输入和路由权重,路由网络采用简单的X*W。
1、路由计算
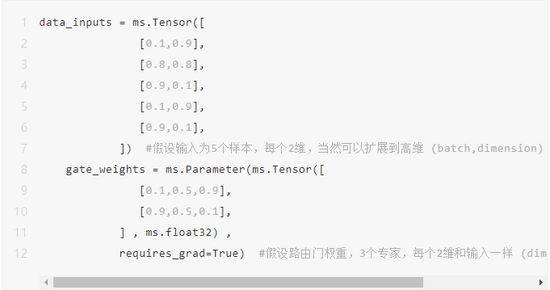
当上述输入5行(仅3类,希望分派给3个专家)样本,和Gate权重做矩阵乘后,可以明确算出每个样本要分派的专家。可以用matmul,也可以类似gates_weighted = einsum('bd,de->be', [data_inputs, gate_weights])第一轮矩阵乘的结果为:
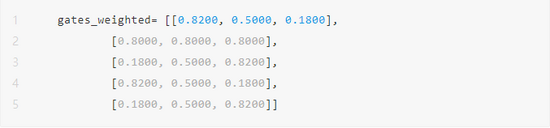
输入和权重乘法,在python中可以采用@,也可以采用matmul,也可以采用爱因斯坦求和简记忆法函数einsum。当是简单的矩阵乘的时候,采用einsum在计算图编译的时候实际会拆分成多个算法,性能并不好;但当输入和权重超过2维,需要以batch维固定做路由计算的时候,使用einsum可以编程实现很简单。
2、分派
条件计算的分派,主要逻辑是根据路由网络的输出,为每个样本计算出top-k的专家。其实现可以通过topk函数实现。由于top选择score可作为后续网络单元的输入信息(含路由的信息),所以一般要对路由输出做softmax做归一化。

按需计算1:all-N专家之间的归一化权重 (please refer to #2) ,gates_weighted一样,按照dim=-1做了归一化而已其输出为:
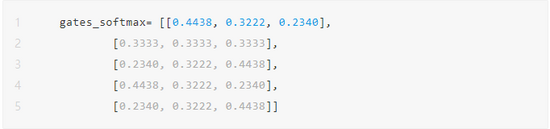
为batch中每个sample选择Top-K个专家 这里为batch中每个的专家权重,可以从softmax-ed来top-k,也可以直接从gates_weighted来top-k;由于这里可能不做softmax或者延后,所以可gates_weighted,这里为batch中每个的专家序号

其输出为:

接着:

按需计算2: top-n专家之间的归一化权重
如何根据分派索引,从原始的输入中,为每个专家提取出属于该专家处理的tensor,在当前的主流智能平台,都没有专门的算子,可以通过其他算子的组合来实现类似的效果。在MindSpore中,可以通过底层的C++实现算子,也可以通过Python中继承Cell并实现bprob, 然后将原始 gate tensor中按照index组织到目标输出中。这里我们实现一个Dispatch类

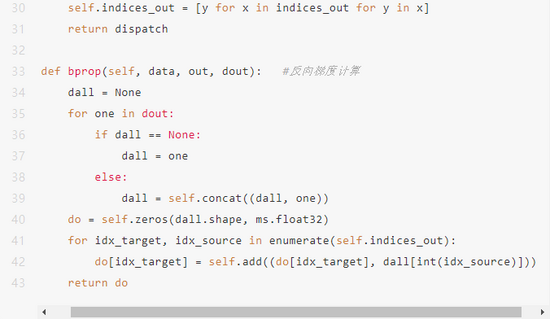
3、独立计算
直接并行调用后续的专家网络。并行部分可以通过平台来支持。可以通过特殊的函数或者annotation等标识,也可以由平台编译时优化为并行执行。(在非动态路由条件计算的网络模型中,一般不存在类似的优化。)
4、合并
合并的逻辑相对简单,先通过cat按照batch维度做拼接,然后构造正确的zeros tensor用index_add按照索引将各个专家网络的结果在保持input序合并到一起,做为该MoE模块的输出。

上述完成了整个MoE的完整计算过程。
代码框架
我们按照上述基本动态路由条件计算的张量操作为主的逻辑,扩展到一个完整的训练代码框架中:
- class Dispatch(ms.nn.Cell): 实现路由中的分派逻辑
- class Combine(ms.nn.Cell): 实现路由中的组装逻辑
- class Route(ms.nn.Cell): 完成整个动态路由逻辑,可以实现为相对通用的类
- class Expert(ms.nn.Cell): 平台用户自定义的专家网络
- class Network(ms.nn.Cell): 平台用户自定义的大网络
- class MSELoss(ms.nn.Cell):实现MSE损失,实现辅助损失的逻辑
- class OutputLossGraph(ms.nn.Cell):输出infer和loss,PyNative模式单步
- class Dataset: 数据集类,仅满足输入shape和X-Y合理对应关系,仅仅示例def train( …): 训练入口
条件计算实现技术点
1、动态路由
- 不可学习路由
如使用LSH (locality sensitive hashing)做路由:在整个可学习网络的前端,使用LSH来分派样本,这样可以避免LSH部分求导问题;如果在网络中间增加LSH模块,需要通过梯度估计完成确定性算法部分梯度传递。
- 可学习路由
简单的做法,定义gate_weights为可学习Parameter,对于二维的张量,通过python@或者matmul等完成权重路由计算;如果是更高维度的张量,且需固定batch维,einsum('bd*,*de->b*e')的形式完成计算。
2、topk和softmax的前后关系
在G_1(x)=softmax(topk(X*W)))和G_2(x)=topk(softmax(X*W)))两类Gate实现中,
将softmax置于Topk前后,对top-k的选择不变;当需要将G_*作为后序网络输入的一部分,即将路由权重信息作为后续网络输入信息,则需要考虑:需要all-N专家之间的归一化权重,则softmax置于top-k之前;否则softmax置于top-k之后,来计算top-N专家之间的归一化权重。
3、如何每专家在批次处理中平衡
按照每样本的路由权重求和,即对batch单个样本被分配的1+个export的重要性和权重求和,计算出importance;按照每样本的路由权重中非0的求和,计算出有负载的专家来求得load。将coefficient_of_variation(importance) + coefficient_of_variation(load)作为auxiliary_loss参与优化,来平衡importance和load。变异系数(Coefficient of Variation)是用于无量纲度量数据的离散程度,越离散在此处表示均衡性越差,需要向更小优化。
在Transformer等多层(多处)MoE的模型中,将多组auxiliary_loss联合作为auxiliary_loss, 在加dominated_loss之后即可。