这篇文章写于我刚学算法时。好家伙,第一道题快排就卡我老半天。但是好消息是,我算是没有得过且过,花了一晚上和一上午,把所有情况都捋了一遍、把迭代过程考虑清楚了。之后便感觉入了门,有了感觉,后续其他题目都没有卡我这么久过。
被很简单的快排 代码运行状态:Memory Limit Exceeded 老半天。
最后琢磨半天越界这事儿。总结起来一句话:避免出现 func(l, r) { ... func(l, r) ... } (递归时传递到下一层的边界值不缩小)这种情况,因为这是死循环。 如何避免?比如func(l, r) { func(l, j), func(j + 1, r)}中,j至少满足 j > r (j从r身上离开,防止 func(l, j) 是 func(l, r)),就可用。
- #include <iostream>
- using namespace std; const int N = 1e6 + 10; int n; int q[N];
- void quick_sort(int q[], int l, int r)
- {
- if (l >= r) return;
- int i = l - 1, j = r + 1, x = q[l + r >> 1];
- while (i < j)
- {
- do i ++; while (q[i] < x);
- do j --; while (q[j] > x);
- if (i < j) swap(q[i], q[j]);
- }
- quick_sort(q, l, j), quick_sort(q, j + 1, r);
- }
- int main() { scanf("%d", &n); for (int i = 0; i < n; i ++) scanf("%d", &q[i]); quick_sort(q, 0, n-1); for (int i = 0; i < n; i ++) printf("%d ", q[i]); return 0; }
手贱,非得写成:
- quick_sort(q, l, i - 1), quick_sort(q, i, r);
好家伙,报错。半天没看出来,后来才恍然大悟,你要是用 i 分界,上面得是 x = q[l + r + 1 >> 1]; 。
那我下面这样不行吗?
- x = q[l+r >> 1];
- ...
- quick_sort(q, l, j - 1), quick_sort(q, j, r);
- // 或者这样不行吗?
- x = q[l+r >> 1];
- ...
- quick_sort(q, l, i - 1), quick_sort(q, i, r);
- // 或者这样不行吗?
- x = q[l+r >> 1];
- ...
- quick_sort(q, l, i), quick_sort(q, i + 1, r);
- // 或者这样不行吗?
- x = q[l+r+1 >> 1];
- ...
- quick_sort(q, l, j), quick_sort(q, j + 1, r);
- // 或者这样不行吗?
- x = q[l+r+1 >> 1];
- ...
- quick_sort(q, l, j - 1), quick_sort(q, j, r);
- // 或者这样不行吗?
- x = q[l+r+1 >> 1];
- ...
- quick_sort(q, l, i), quick_sort(q, i + 1, r);
上述都不行,看我一一举反例。
我们输入长度是2的数组,则第一层循环:l = 0, r = 1(即 quick_sort(0, 1)),如果进入第二层循环时,还出现 quick_sort(0, 1)的情况,则陷入死循环。
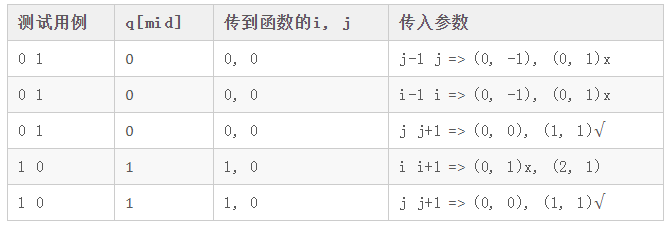
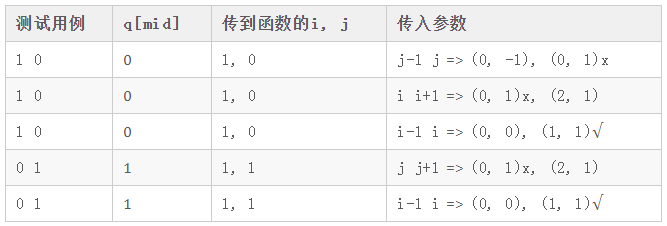
下表中,“传到函数的i, j”指调用 quick_sort(q, l, ?i/j), quick_sort(q, ?i/j, r) 中 i, j 的值。
下表中,最后一列标记 x 表示将使程序陷入死循环。
对于 int mid = l+r >> 1;:
可见,在 int mid = l+r >> 1; 时,四种组合中只有 j j+1 经受住了 0 1 和 1 0 的双重考验。
对于 int mid = l+r+1 >> 1;:
可见,在 int mid = l+r+1 >> 1; 时,四种组合中只有 i-1 i 经受住了 0 1 和 1 0 的双重考验。
这是为什么呢?
- 这里有相关证明:AcWing 785. 快速排序算法的证明与边界分析[1]
- 如果你没耐心看上述较为严谨的证明,可以看文末我写的
我用比较笨的方法理解是:
- int mid = l+r >> 1;:则可证明 j 的取值范围是 [l, r-1] ,因此对于边界组合 j j+1 有 quick_sort(q, l, j小于r), quick_sort(q, j+1大于l, r) ,永远都不会有 quick_sort(q, l, r) 出现。
- int mid = l+r+1 >> 1;:则可证明 i 的取值范围是 [l+1, r] ,因此对于边界组合 i-1 i 有 quick_sort(q, l, i-1小于r), quick_sort(q, i大于l, r) ,永远都不会有 quick_sort(q, l, r) 出现。
OK,那下面就是背诵:
- 快排中,int mid = l+r >> 1;( mid 向下取整),是 j j+1,因为j 取值范围是 [l r-1]
- 我个人是不太喜欢背诵的,还是知道原理,觉得到时候可以快速推导出来靠谱,推导如下。
用较清晰但是笨拙的方法证明一下 mid 向下取整时 j 属于 [l, r-1]。
向下取整时 j 属于 [l, r-1] ==等价于== 向下取整时至少有两次 j-- 被执行
下面分三种特殊情况讨论(普通情况不讨论),可以看出三种情况中都至少有两次 j-- 被执行
情况1:j在r处就不再q[j] > x,而i在l处还满足q[i] < x
- q[mid] x
- 9 8
- begin i j
- step1 i j do i++; while(q[i] < x);
- step2 i j do j--; while(q[j] > x);
- step3 8 9
- step4 i j swap(q[i], q[j]);
- step5 ij do i++; while(q[i] < x);
- step6 j i do j--; while(q[j] > x);
- 跳出循环 while(i < j) {}
j在r处就不再q[j] > x,而i在l处还满足q[i] < x;因此对于l < r,还要再跳一轮,因为是 do while 而不是 while do ,所以不管 i 或 j 什么条件,都得再至少来一次 i++; j--; 。
情况2:j在r处还满足q[j] > x,而i在l处就不再q[i] < x
- q[mid] x
- 8 9
- begin i j
- step1 i j do i++; while(q[i] < x);
- step2 ij do j--; while(q[j] > x);
- step3 8 9
- 跳出循环 while(i < j) {}
j在r处还满足q[j] > x,因此,一定会继续执行j--,j一定会小于r。
情况3:j在r处就不再q[j] > x,且i在l处就不再q[i] < x
- q[mid] x
- 8 8
- begin i j
- step1 i j do i++; while(q[i] < x);
- step2 i j do j--; while(q[j] > x);
- step3 8 8
- step4 i j swap(q[i], q[j]);
- step5 ij do i++; while(q[i] < x);
- step6 j i do j--; while(q[j] > x);
- 跳出循环 while(i < j) {}
j在r处就不再q[j] > x,且i在l处就不再q[i] < x;此时有 i < j ,因此不跳出循环,执行 swap;对于l < r,还要再跳一轮,因为是 do while 而不是 while do ,所以不管 i 或 j 什么条件,都得再至少来一次 i++; j--; 。
这里的魅力在于 do while :不管咋的,你满不满足条件,我先给你移动一下,你再判断。
对于二分法,核心思想也是避免出现func(l, r) { func(l, r); } ,因此出现 mid = l + r >> 1; 则必有 r = mid; ,因为 mid 是向下取整,l < r 时 mid 肯定碰不到 r 。