用定租问题学透K近邻算法

 [[405033]]

k近邻思想是我觉得最纯粹最清晰的一个思想，k近邻算法(KNN)只是这个思想在数据领域都一个应用。

你的工资由你周围的人决定。

你的水平由你身边最接近的人的水平决定。

你所看到的世界,由你身边的人决定。

思想归思想，不能被编码那也无法应用于数据科学领域。

我们提出问题，然后应用该方法加以解决，以此加深我们对方法的理解。

问题： 假设你是airbnb平台的房东，怎么给自己的房子定租金呢?

分析： 租客根据airbnb平台上的租房信息，主要包括价格、卧室数量、房屋类型、位置等等挑选自己满意的房子。给房子定租金是跟市场动态息息相关的，同样类型的房子我们收费太高租客肯定不租，收费太低收益又不好。

解答： 收集跟我们房子条件差不多的一些房子信息，确定跟我们房子最相近的几个，然后求其定价的平均值，以此作为我们房子的租金。

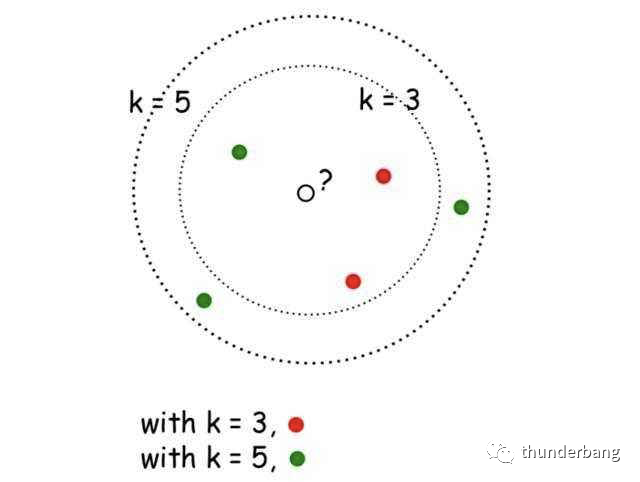
这就是K-Nearest Neighbors(KNN)，k近邻算法。KNN的核心思想是未标记样本的类别，由距离其最近的k个邻居投票决定。

本文就基于房租定价问题梳理下该算法应用的全流程，包含如下部分。

1. 读入数据
2. 数据处理
3. 手写算法代码预测
4. 利用sklearn作模型预测
5. 超参优化
6. 交叉验证
7. 总结

提前声明，本数据集是公开的，你可以在网上找到很多相关主题的材料，本文力图解释地完整且精准，如果你找到了更详实的学习材料，那再好不过了。

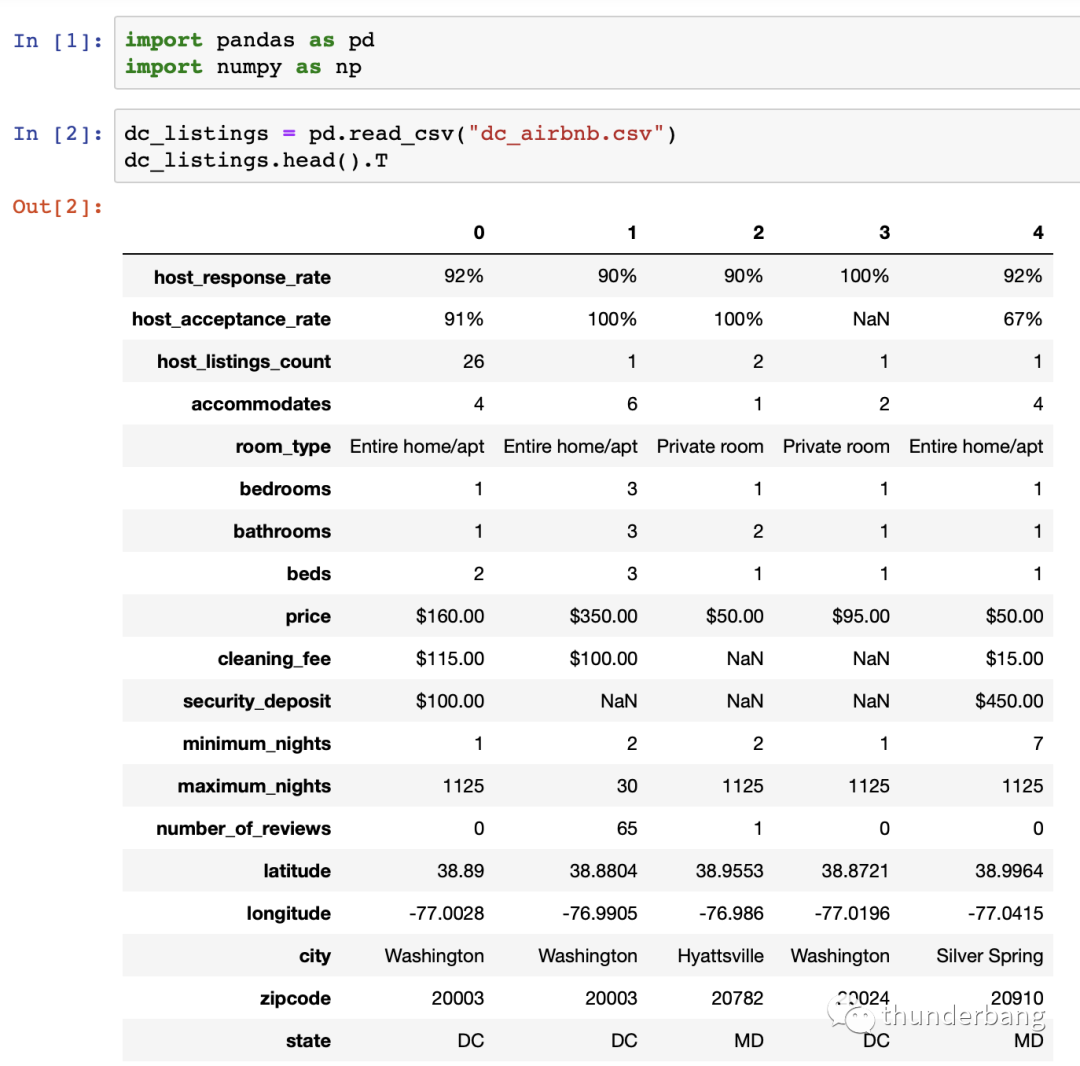
1.读入数据

先读入数据，了解下数据情况，发现目标变量price，以及cleaning_fee和security_deposit的格式有点问题，另有一些变量是字符型，都需要处理。我对dataframe进行了转置显示，方便查看。

2.数据处理

我们先只处理price，尽量集中在算法思想本身上面去。

# 处理下目标变量price，并转换成数值型 
stripped_commas = dc_listings['price'].str.replace(',', '') 
stripped_dollars = stripped_commas.str.replace('$', '') 
dc_listings['price'] = stripped_dollars.astype('float') 
 
# k近邻算法也是模型，需要划分训练集和测试集 
sample_num = len(dc_listings) 
# 在这我们先把数据随机打散，保证数据集的切分随机有效 
dc_listings = dc_listings.loc[np.random.permutation(len(sample_num))] 
train_df = dc_listings.iloc[0:int(0.7*sample_num)] 
test_df = dc_listings.iloc[int(0.7*sample_num):] 

3.手写算法代码预测

根据k近邻算法的定义直接编写代码，从简单高效上考虑，我们仅针对单变量作预测。

入住人数应该是和租金关联度很高的信息，面积应该也是。我们这里采用前者。

我们的目标是理解算法逻辑。实际操作中一般不会只考虑单一变量。

# 注意，这儿是train_df 
def predict_price(new_listing): 
    temp_df = train_df.copy() 
    temp_df['distance'] = temp_df['accommodates'].apply(lambda x: np.abs(x - new_listing)) 
    temp_df = temp_df.sort_values('distance') 
    nearest_neighbor_prices = temp_df.iloc[0:5]['price'] 
    predicted_price = nearest_neighbor_prices.mean() 
    return(predicted_price) 
 
# 这儿是test_df 
test_df['predicted_price'] = test_df['accommodates'].apply(predict_price) 
# MAE(mean absolute error), MSE(mean squared error), RMSE(root mean squared error) 
test_df['squared_error'] = (test_df['predicted_price'] - test_df['price'])**(2) 
mse = test_df['squared_error'].mean() 
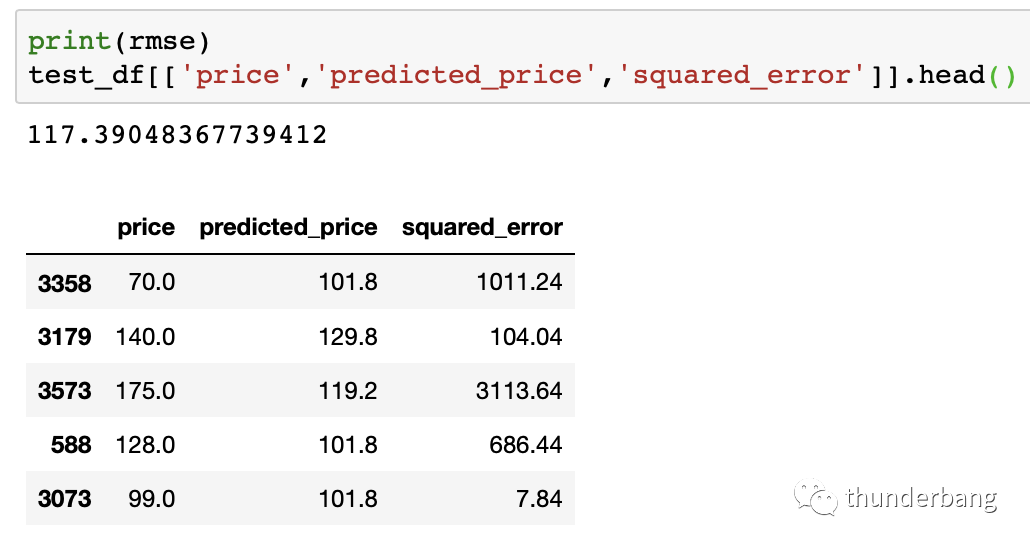
rmse = mse ** (1/2) 

值得强调的是，模型算法的构建都是基于训练集的，预测评估基于测试集。应用评估严格上还有一类样本，oot：跨时间样本。

从结果来看，即使我们只用了入住人数accommodates这一个变量去做近邻选择，预测结果也是很有效的。

4.利用sklearn作模型预测

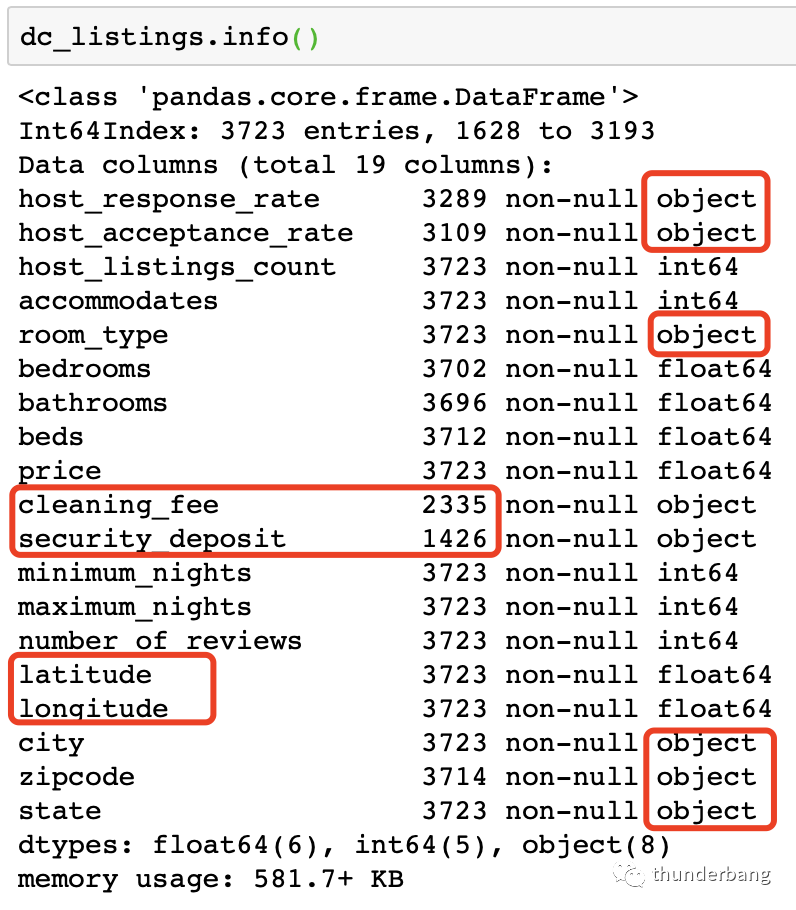
这次我们要用更多的变量，只剔掉字符串和不可解释的变量，剩下能用的变量都用上。

当用了多个变量的时候，这些不变量纲是不一样的，我们需要进行标准化处理。保证了各自变量的分布差异，同时又保证变量之间可叠加。

# 剔掉非数值型变量和不合适的变量 
drop_columns = ['room_type', 'city', 'state', 'latitude', 'longitude', 'zipcode', 'host_response_rate', 'host_acceptance_rate', 'host_listings_count'] 
dc_listings = dc_listings.drop(drop_columns, axis=1) 
# 剔掉缺失比例过高的列（变量） 
dc_listings = dc_listings.drop(['cleaning_fee', 'security_deposit'], axis=1) 
# 剔掉有缺失值的行（样本） 
dc_listings = dc_listings.dropna(axis=0) 
# 多个变量的量纲不一样，需要标准化 
normalized_listings = (dc_listings - dc_listings.mean())/(dc_listings.std()) 
normalized_listings['price'] = dc_listings['price'] 
 
# 于是我们得到了可用于建模的数据集，7：3划分训练集测试集 
train_df = normalized_listings.iloc[0:int(0.7*len(normalized_listings))] 
test_df = normalized_listings.iloc[int(0.7*len(normalized_listings)):] 
# price是y，其余变量都是X 
features = train_df.columns.tolist() 
features.remove('price') 

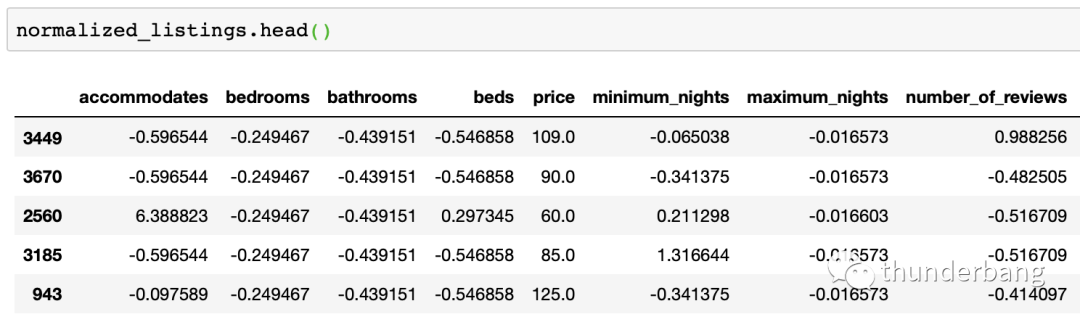
处理后的数据集如下，其中price是我们要预测的目标，其余是可用的变量。

from sklearn.neighbors import KNeighborsRegressor 
from sklearn.metrics import mean_squared_error 
 
knn = KNeighborsRegressor(n_neighbors=5, algorithm='brute') 
knn.fit(train_df[features], train_df['price']) 
predictions = knn.predict(test_df[features]) 
mse = mean_squared_error(test_df['price'], predictions) 
rmse = mse ** (1/2) 

最后得到的rmse=111.9，相比单变量knn的117.4要小，结果得到优化。严格来说，这个对比不完全公平，因为我们丢掉了少量的特征缺失样本。

5.超参优化

在第3和第4部分，我们预设了k=5，但这个拍脑袋确定的。该取值合不合理，是不是最优，都需要进一步确定。

其中，这个k就是一个超参数。对于任何一个数据集，只要你用knn，就需要确定这个k值。

k值不是通过模型基于数据去学习得到的，而是通过预设，然后根据结果反选确定的。任何一个超参数都是这样确定的，其他算法也如此。

import matplotlib.pyplot as plt 
%matplotlib inline 
 
hyper_params = [x for x in range(1,21)] 
rmse_values = [] 
features = train_df.columns.tolist() 
features.remove('price') 
 
for hp in hyper_params: 
    knn = KNeighborsRegressor(n_neighbors=hp, algorithm='brute') 
    knn.fit(train_df[features], train_df['price']) 
    predictions = knn.predict(test_df[features]) 
    mse = mean_squared_error(test_df['price'], predictions) 
    rmse = mse**(1/2) 
    rmse_values.append(rmse) 
     
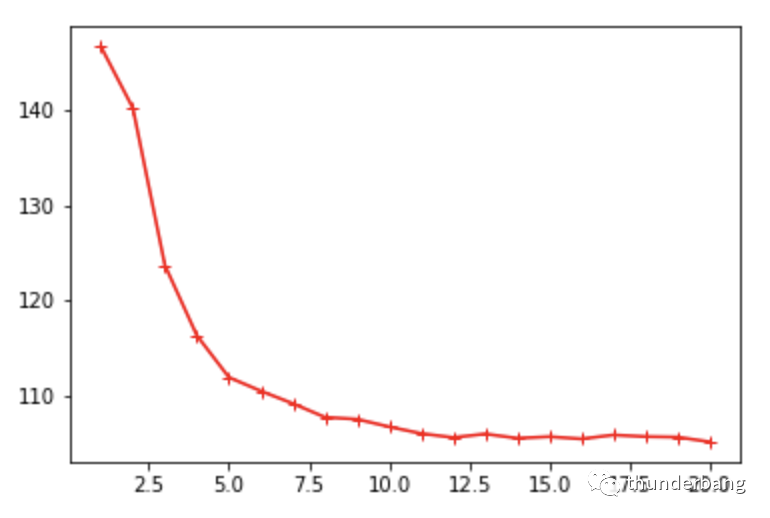
plt.plot(hyper_params, rmse_values,c='r',linestyle='-',marker='+') 

我们发现，k越大，预测价格和真实价格的偏差从趋势看会更准确。但要注意，k越大计算量就越大。

我们在确定k值时，可以用albow法，也就是看上图的拐点，形象上就是手肘的肘部。

相比k=5，k=7或10可能是更好的结果。

6.交叉验证

上面我们的计算结果完全依赖训练集和测试集，虽然对它们的划分我们已经考虑了随机性。但一次结果仍然具备偶尔性，尤其是当样本量不够大时。

交叉验证就是为了解决这个问题。我们可以对同一个样本集进行不同的训练集测试集划分。每次划分后都重新进行训练和预测，然后综合去看待这些结果。

应用最广泛的是n折交叉验证，其过程是随机将数据集切分成n份，用其中n-1个子集做训练集，剩余1个子集做测试集。这样一共可以进行n次训练和预测。

我们可以直接手写该逻辑，如下。

sample_num = len(normalized_listings) 
normalized_listings.loc[normalized_listings.index[0:int(0.2*sample_num)], "fold"] = 1 
normalized_listings.loc[normalized_listings.index[int(0.2*sample_num):int(0.4*sample_num)], "fold"] = 2 
normalized_listings.loc[normalized_listings.index[int(0.4*sample_num):int(0.6*sample_num)], "fold"] = 3 
normalized_listings.loc[normalized_listings.index[int(0.6*sample_num):int(0.8*sample_num)], "fold"] = 4 
normalized_listings.loc[normalized_listings.index[int(0.8*sample_num):], "fold"] = 5 
 
fold_ids = [1,2,3,4,5] 
def train_and_validate(df, folds): 
    fold_rmses = [] 
    for fold in folds: 
        # Train 
        model = KNeighborsRegressor() 
        train = df[df["fold"] != fold] 
        test = df[df["fold"] == fold].copy() 
        model.fit(train[features], train["price"]) 
        # Predict 
        labels = model.predict(test[features]) 
        test["predicted_price"] = labels 
        mse = mean_squared_error(test["price"], test["predicted_price"]) 
        rmse = mse**(1/2) 
        fold_rmses.append(rmse) 
    return(fold_rmses) 
 
rmses = train_and_validate(normalized_listings, fold_ids) 
avg_rmse = np.mean(rmses) 

工程上，我们要充分利用工具和资源。sklearn库就包含了我们常用的机器学习算法实现，可以直接用来验证。

from sklearn.model_selection import cross_val_score, KFold 
kf = KFold(5, shuffle=True, random_state=1) 
model = KNeighborsRegressor() 
mses = cross_val_score(model, normalized_listings[features], normalized_listings["price"], scoring="neg_mean_squared_error", cv=kf) 
rmses = np.sqrt(np.absolute(mses)) 
avg_rmse = np.mean(rmses) 

交叉验证的结果置信度会更高，尤其是在小数据集上。因为它能够一定程度地减轻偶然性误差。

结合交叉验证和超参优化，我们一般就得到了该数据集下用knn算法预测的最优结果。

# 超参优化 
num_folds = [x for x in range(2,50,2)] 
rmse_values = [] 
 
for fold in num_folds: 
    kf = KFold(fold, shuffle=True, random_state=1) 
    model = KNeighborsRegressor() 
    mses = cross_val_score(model, normalized_listings[features], normalized_listings["price"], scoring="neg_mean_squared_error", cv=kf) 
    rmses = np.sqrt(np.absolute(mses)) 
    avg_rmse = np.mean(rmses) 
    std_rmse = np.std(rmses) 
    rmse_values.append(avg_rmse) 
     
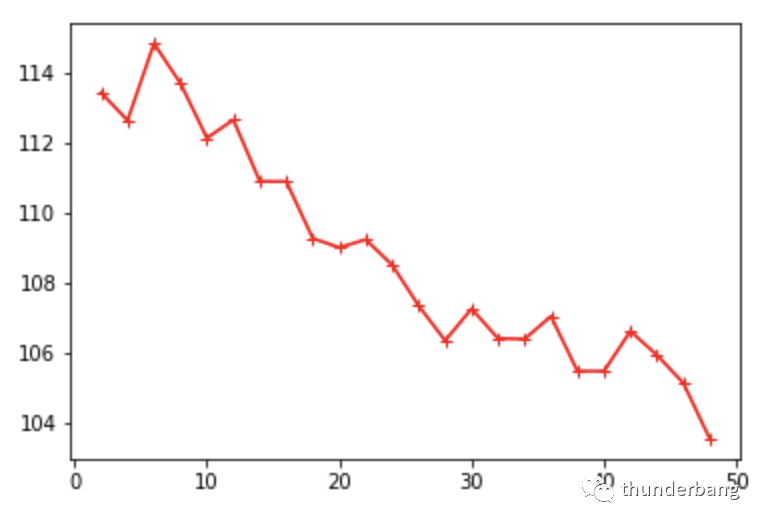
plt.plot(num_folds, rmse_values,c='r',linestyle='-',marker='+') 

我们得到了相同的趋势，k越大，效果趋势上更好。同时因为交叉验证一定程度上解决了过拟合问题，理想的k值越大，模型可以更复杂些。

7.总结

从k-近邻算法的核心思想以及以上编码过程可以看出，该算法是基于实例的学习方法，因为它完全依靠训练集里的实例。

该算法不需什么数学方法，很容易理解。但是非常不适合应用在大数据集上，因为k-近邻算法每一次预测都需要计算整个训练集的数据到待预测数据的距离，然后增序排列，计算量巨大。

如果能用数学函数来描述数据集的特征变量与目标变量的关系，那么一旦用训练集获得了该函数表示，预测就是简简单单的数学计算问题了。计算复杂度大大降低。

其他的经典机器学习算法基本都是一个函数表达问题。后面我们再看。

本文转载自微信公众号「 thunderbang」，可以通过以下二维码关注。转载本文请联系 thunderbang公众号。