本文转载自微信公众号「程序员小熊」,作者程序员小熊。转载本文请联系程序员小熊公众号。
前言
大家好,我是来自华为的「程序员小熊」。相信绝大部分童鞋都知道,在处理与「链表」相关问题时,常用的解题套路主要包括「双指针」、「迭代」和「虚拟头节点」等等。
今天「小熊」主要介绍采用「递归」的策略,秒杀「链表」相关问题,使得代码更「优雅」,并以两道常见的面试题作为例题来讲解,供大家参考,希望对大家有所帮助。
链表与递归
链表具有天然的递归性,一个链表可以看出头节点后面挂接一个更短的链表,这个更短的链表是以原链表的头节点的下一节点为头节点,依次内推,直到最后的更短的链表为空,空本身也是一个链表(最基础的)。
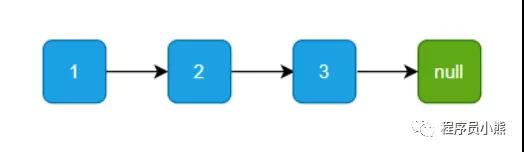
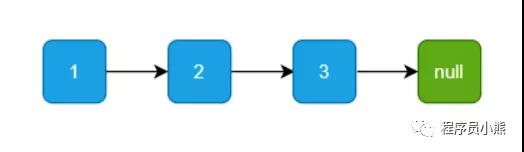
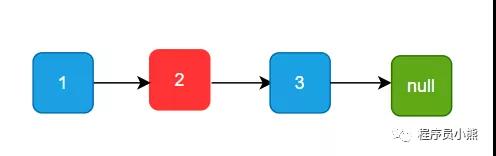
以单链表 1->2->3->null 为例子,如下图示:
原链表
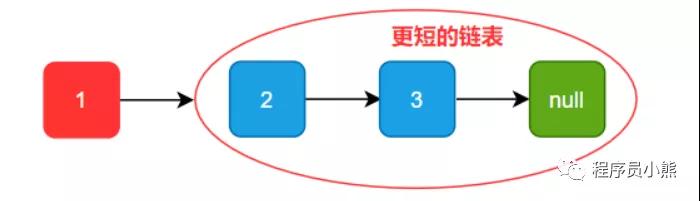
将原链表看出头节点 1 后挂接一个更短的链表
头节点+更短链表
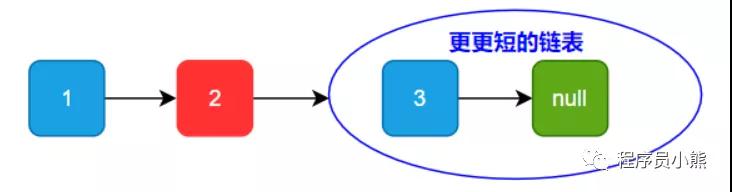
继续拆解,直到无法拆解
更更短链表
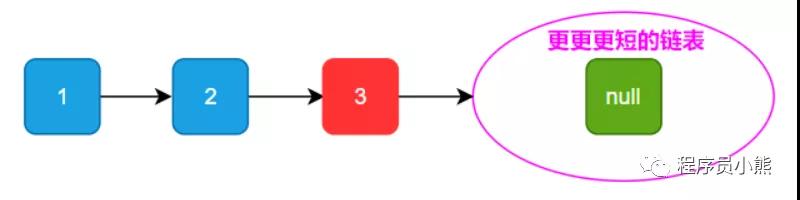
更更更短链表
有了这样的思考,很多「链表」相关问题,都可以采用「递归」的思路来解答。
剑指 Offer 24. 反转链表
- 定义一个函数,输入一个链表的头节点,反转该链表并输出反转后链表的头节点。
- 示例:
- 输入: 1->2->3->4->5->NULL
- 输出: 5->4->3->2->1->NULL
- 限制:
- 0 <= 节点个数 <= 5000
解题思路
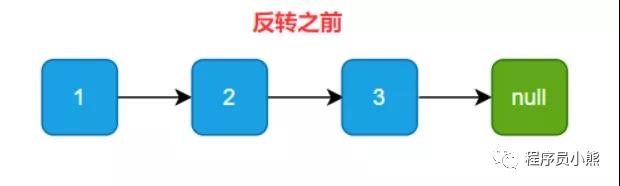
要反转链表,即将原链表的头节点变为新链表的尾节点,原链表的尾节点变为新链表的头节点。如下图示:
反转之前:
原链表
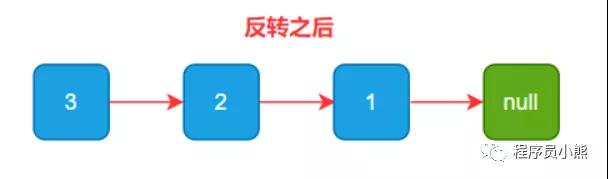
反转之后:
新链表
主要策略主要有:1、直接修改链表的值,如上图中的原链表图所示,将原链表值 1 的头节点改为原链表尾节点的值,依次类推;2、让遍历整个链表,让链表的尾节点指向其前一个节点,依次类推。
虽然这两个策略都可行,不过在面试中通常要求采用「策略2」。
由上面的「递归与链表」可知,本题也可以采用「递归法」去求解。
具体如何通过「递归」去解答呢?见下面例子。
「举例」
链表 1->2->3->null 为例子,如下图示。
示例
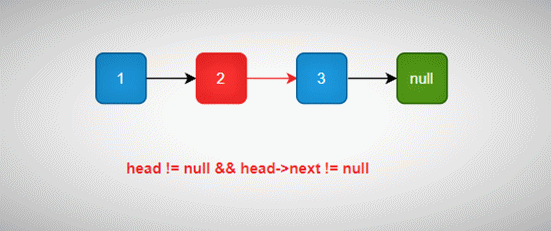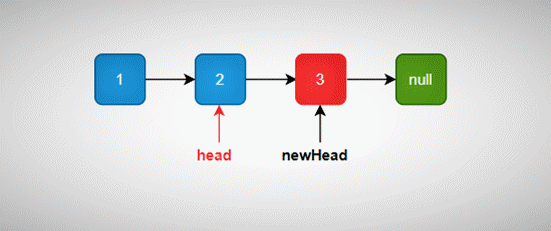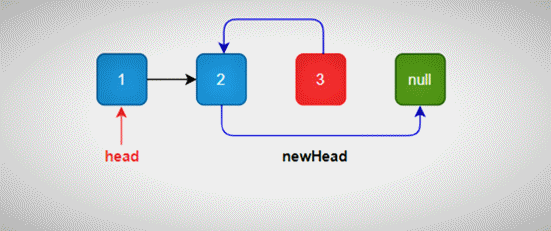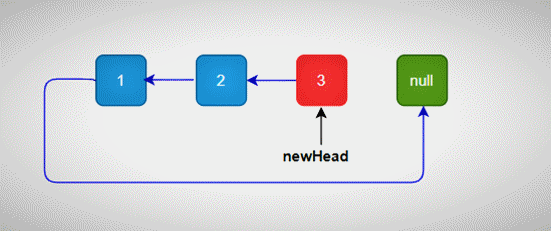
不断遍历找到原链表为尾节点,即新链表的头节点。
原链表尾节点
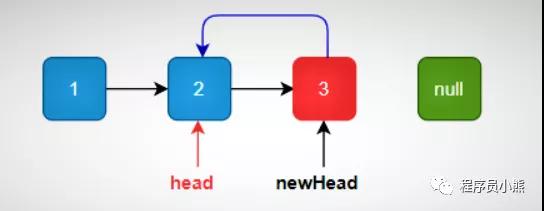
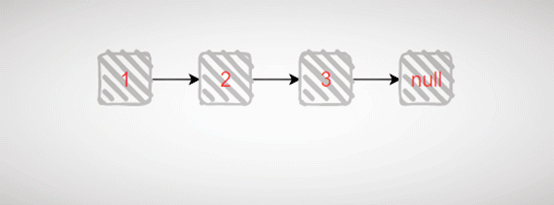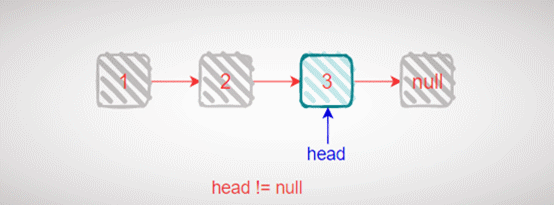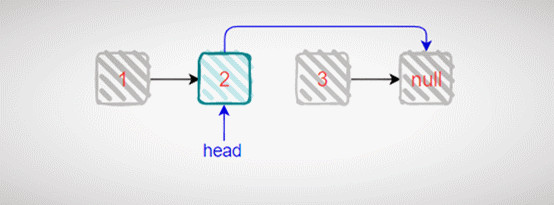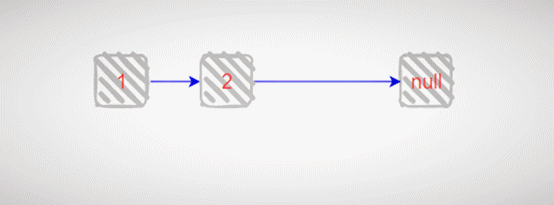
然后让尾节点指向其前驱节点,依次类推。
递归反转
详细步骤,如下动图示:
递归反转单链表
Show me the Code
「C」
- struct ListNode* reverseList(struct ListNode* head){
- /* 递归终止条件 */
- if (head == NULL || head->next == NULL) {
- return head;
- }
- /* 反转当前所在的链表节点 */
- struct ListNode* newHead = reverseList(head->next);
- /* 由原链表的尾节点挨个指向其前驱节点 */
- head->next->next = head;
- /* 防止成环 */
- head->next = NULL;
- /* 返回新的链表头节点 */
- return newHead;
- }
「java」
- ListNode reverseList(ListNode head) {
- if (head == null || head.next == null) {
- return head;
- }
- ListNode node = reverseList(head.next);
- head.next.next = head;
- head.next = null;
- return node;
- }
当然本题也可以采用「迭代」的方法去做,其代码(python 版)也很优雅,具体如下:
Show me the Code
「python」
- def reverseList(self, head: ListNode) -> ListNode:
- cur, pre = head, None
- while cur:
- cur.next, pre, cur = pre, cur, cur.next
- return pre
「复杂度分析」
时间复杂度:「O(n)」,n 是链表的长度。对链表的每个节点都进行了反转操作。
空间复杂度:「O(n)」,n 是链表的长度。递归调用的栈空间,最多为 n 层。
203. 移除链表元素
- 给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足
- Node.val == val 的节点,并返回 新的头节点 。
- 示例 1:
- 输入:head = [1,2,6,3,4,5,6], val = 6
- 输出:[1,2,3,4,5]
- 示例 2:
- 输入:head = [], val = 1
- 输出:[]
- 示例 3:
- 输入:head = [7,7,7,7], val = 7
- 输出:[]
解题思路
要移除链表中给定值的节点,一般策略是「找到给点值的节点的前驱节点,然后让其指向给定值的节点的后继节点」。
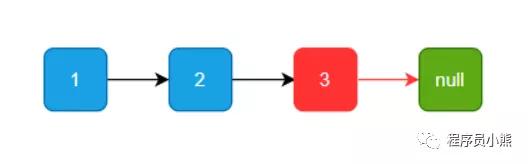
例如要删除链表 1->2->3->null 中,节点值为 3 的节点,就得先找到其前驱节点(值为 2 的节点),如下图示:
删除给定值的节点
由上面的「递归与链表」可知,本题同样也可以采用「递归法」去求解,不断删除更短链表中给定值的节点,然后再将处理后的更短的链表,挂接在其前驱节点后。
「注意」最后要判断原链表的头节点是否是待移除的节点。
「举例」
以链表 1->2->3->null 为例子,移除链表中给定值的节点的过程,如下动图示。
示例动图
Show me the Code
「C++」
- ListNode* removeElements(ListNode* head, int val) {
- /* 递归终止条件 */
- if(head == NULL) {
- return NULL;
- }
- /* 删除链表中头节点后值为 val 的元素的节点 */
- head->next=removeElements(head->next,val);
- /* 判断头节点是否为值为 val 的节点,再返回*/
- return head->val==val ? head->next : head;
- }
「Golang」
- func removeElements(head *ListNode, val int) *ListNode {
- if head == nil {
- return head
- }
- head.Next = removeElements(head.Next, val)
- if head.Val == val {
- return head.Next
- }
- return head
- }
「复杂度分析」
时间复杂度:「O(n)」,n 是链表的长度。递归需要遍历链表一次。
空间复杂度:「O(n)」,n 是链表的长度。递归调用栈,最多不会超过 n 层。