本文转载自微信公众号「数据STUDIO」,作者云朵君。转载本文请联系数据STUDIO公众号。
在本文中,重点介绍特征选择方法基于评估机器学习模型的特征重要性在各种不可解释(黑盒)及可解释机器学习方法上的表现。比较了CART、Optimal Trees、XGBoost和SHAP正确识别相关特征子集的能力。
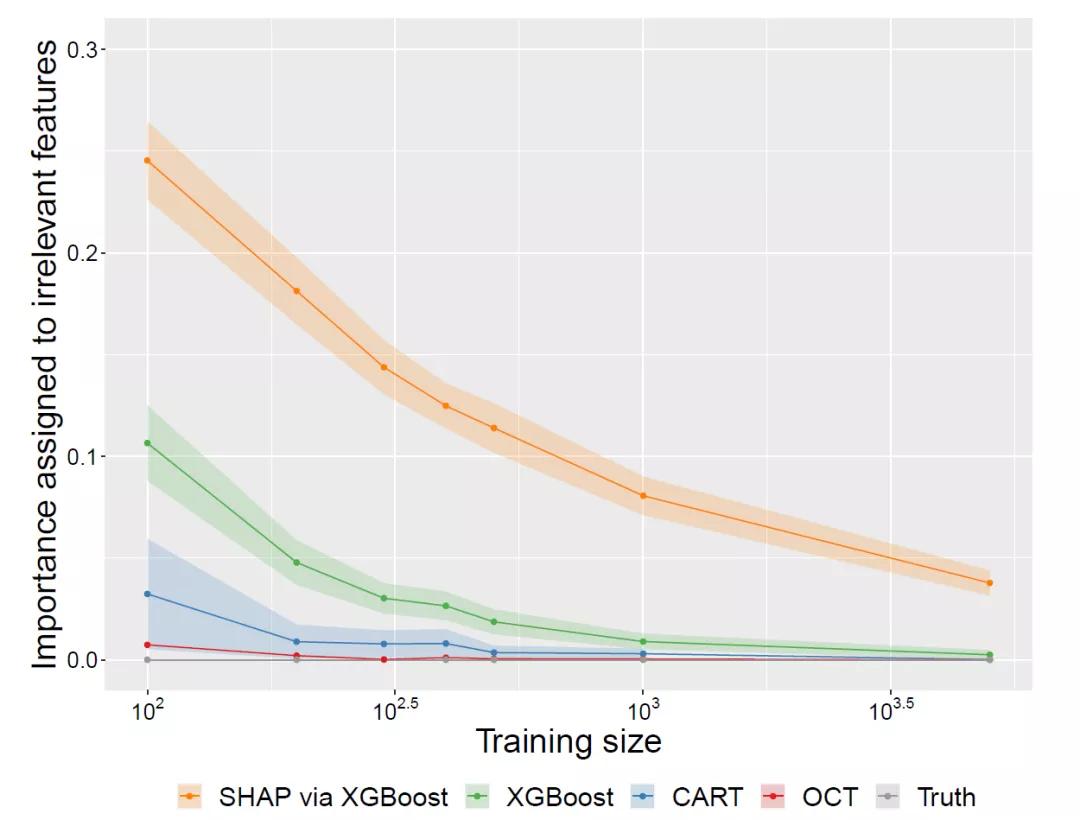
无论使用原生特征重要性方法还是SHAP、 XGBoost都不能清晰地区分相关和不相关的特征。而可解释方法(interpretable methods)能够正确有效地识别无关特征,从而为特征选择提供了显著的良好的性能。
特征选择
在物联网的时代,每天都在以越来越快的速度创建和收集数据,这导致与每个数据点相关的数据集具有成千上万的特征。虽然众多机器学习和人工智方法能都拥有强大的预测能力,但在这种高维数据集中,模型在理解各种特征的相对质量时,也会变得很复杂。事实上,在训练模型时并不需要用到所有的高维数据集,而运用其中一小部分特征来训练模型也可以得到大部分或所有的预测性能。
特征选择(feature selection)从所有的特征中,选择出意义的,对模型有帮助的特征,以避免必须将所有特征都导入模型中去训练的情况。
我们一般有四种方法可以选择:过滤法、嵌入法、包装法和降维法。其中包装法和嵌入法都是依赖于依赖于算法自身的选择,即基于评估机器学习模型的特征重要性,根据重要性分数了解哪些特征与做出预测最相关的方法。这也是最常用的特征选择方法之一。
特征选择的重要性并不需要过多描述,因此由模型计算出的重要性分数能否反映实际情况是至关重要的。错误地高估不相关特征的重要性会导致错误的发现,而低估相关特征的重要性会导致我们丢弃重要的特征,从而导致模型性能较差。
此外,像XGBoost这样的黑盒模型提供了更加先进的预测性能,但人类并不容易理解其内在原理,因需要依赖于特征重要性分数或SHAP之类的可解释性方法来研究他们对特征选择的行为。
基于评估器计算特征重要性原理
前面已经说过最常用的特征选择方法之一是基于评估机器学习模型的特征重要性,而评估机器学习模型试图量化每个特征的相对重要性,以预测目标变量。特征重要性的计算方式是通过度量模型中每个特性的使用所带来的性能增量改进来,并在整个模型中总结这些信息。我们可以使用它来识别那些被认为很少或不重要的特性,并将它们从模型中删除。
不足之处:任何特征选择的方法只有在它也是准确的时候才有用。
CART树特征选择的优缺点
基于树的模型是机器学习中最常用的方法之一,因为它们的能力和可解释性。CART等单树模型是完全可解释的,因为可以很容易地通过观察最终决策树中的分割来遵循它们的预测逻辑。
然而,CART是使用每次形成一个分割的树的贪婪启发式方法进行训练模型的,这种方法会产生许多缺点。
- 首先,这可能导致树远不是全局最优的,因为贪婪启发式中任何给定点上的最佳分割,这已被证明在树的未来生长环境中并不是最佳的选择。
- 其次,由于CART算法采用每一步都穷尽搜索所有特征来拆分选择方法,所以倾向于选择拆分点较多的特征。由于特征的选择很可能会偏向那些具有大量唯一值的特征,而贪婪算法可能导致在树根附近的被用于分割数据的特征选择错误,而这些特征往往是最重要的。
基于树的集成学习器
基于树的集成方法,如随机森林和梯度增强(如XGBoost),通过集成大量单树模型的预测来改进CART的性能。这样确实带来了更为先进的性能,但牺牲了模型的可解释性,因为人类几乎不可能理解成百上千的树模型之间的交互及其他行为。因此,通常需要依赖可变重要性方法来理解和解释这些模型的工作机制。
这些模型在计算特征重要性时,可能会存在一定的敏感性,尤其对具有很多潜在分裂点的特征,及特征中包含一些易形成偏倚问题的数据。
SHAP
SHAP是一种最新的方法,它统一了许多早期的方法,旨在解决集成树模型中的偏倚问题,并使用博弈论方法来理解和解释每个特性是如何驱动最终预测的。SHAP因为它的鲁棒性和解决偏差问题,迅速被广泛用于解释黑箱模型和进行特征选择。
最优树
如前所述,与集成方法相比,CART的预测性能较差,但集成方法被迫牺牲单个决策树的可解释性来实现较好的预测性能,这使得从业者不得不在性能和可解释性之间进行选择。
最优树利用混合整数优化在单步构造全局最优决策树。所得到的模型不仅保持了单个决策树的可解释性,又能达到黑盒模型一样的高性能。
由于该方法考虑同时优化树中的所有分割,而不是贪婪地一个一个地优化,我们可以预期分割选择,不像CART那样容易受到同样的偏倚问题的影响。
对比结果
SHAP和XGBoost一直低估关键特征的重要性,而将不相关的特征赋予显著的重要性,并且在较高的噪声下无法完全区分相关与不相关的特征。显然这些不能被用于特征选择或解释,否则这将会发生严重的后果。
另一方面,可解释的单树模型在识别与预测无关的特征方面优势突出,在需要相对较少的训练数据的情况下将其重要性降至零。
相对于CART树,最优树注重全局优化,因而其识别无关特征的速度更快以及对特征选择的偏倚问题的敏感性更低。
可解释的单树模型在消除无关特征方面是完全透明和有效的;在使用最优树时,通常以很少甚至没有性能代价就能完成消除无关特征。
参考:
Comparing interpretability and explainability for feature selection
Interpretable AI Cambridge, MA 02142,Jack Dunn etc.