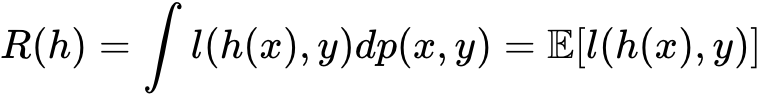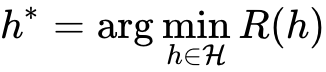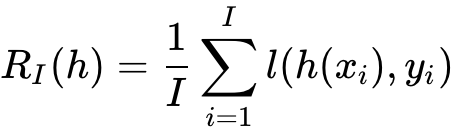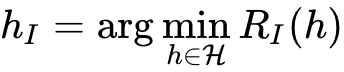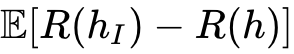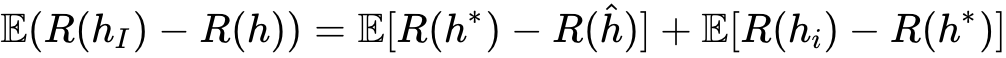今天深度学习之所以成功,大量的数据是不可缺少的必要条件。我们训练的模型都是吃过见过后才有现在这样良好的表现。不过实际情况要收集到足够多的数据并非易事,今天我们就这个问题来学习 Few-shot Learning。
上面的公式是用于估测模型,通常我们输入一个公式 x 给函数 h,这个函数 h 是模型学习到的。然后这个 L 表示预测值和真实值之间的差值,对这个差值在整个数据样本上求积分来评估这个函数 h 的拟合程度。
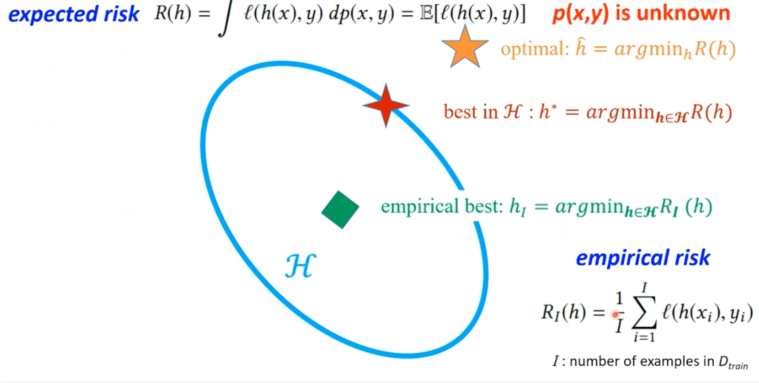
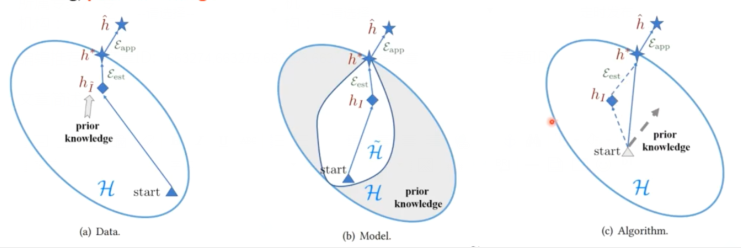
可以利用上面公式来找让 R(h) 最小时,所对应的函数 h,实际是无法遍历所有的模型和参数,所以需要函数集进行限制,从而缩小模型在整个空间搜索范围。这里 H 表示我们定义一个函数集,也就是在整个空间内划分出一定空间,模型搜索问题将仅限定在这个空间内进行。函数集 H 可以是 VGG、ResNet 等,函数集越复杂也就是函数表达能力越强,在整个空间所占范围也就是越大,浅蓝色圈就越大,同时搜索时间也会更长。其实对于样本的概率分布也是未知的,我们收集的样本只是数据的一部分。
那么现在就是将搜索最优函数限定在 H 空间进行搜索了。之前我们已经知道了数据的概率p(x,y) 分布也是未知的。我们只能以一定数量的样本来估计总体分布情况,当然这样做也是存在误差的。
因为对于整个数据集概率分布是未知的,所以用 I 样本代表着整体数据集。然后使用这些数据来训练出一个模型。
然后在这样的数据集上在限定空间内搜索出一个最优函数用绿色块表示搜索到模型在整个搜索空间的位置。
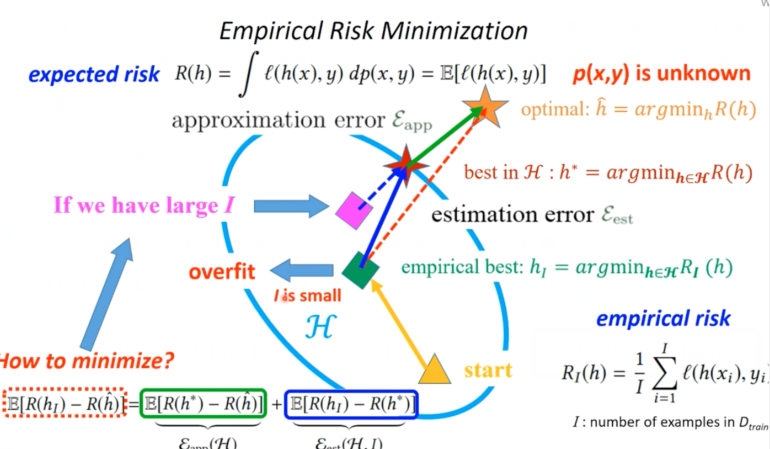
接下里就从黄色 start 开始在搜索空间进行搜索到在 I 样本的数据集上得到函数 h 下标 l 整个函数。那么橘黄色虚线表示真实模型和我们估计的模型之间差距表示为
其实这里误差分别来源于近似误差(approximation error)和估计误差(estimation error)
第一步我们选择一个函数集,那么什么是函数集呢,例如 VGG、ResNet 或者 DenseNet 这些都可以看成一个函数集 H,那么在整个算法中我们能够控制的是 I 和 H。所以我们可以通过增加 H 复杂性也就是扩大 H 空间以及增加 I,不过通常情况下实际我们能够收集到 I 都会很小。
- 所以今天出现了过拟合的最直接的方式就是增加数量,也就是加大 I (数据)
- 也就是为 H 添加一些约束空间,缩小搜索空间(模型)
- 还有就是合理给出一个初始值(算法)