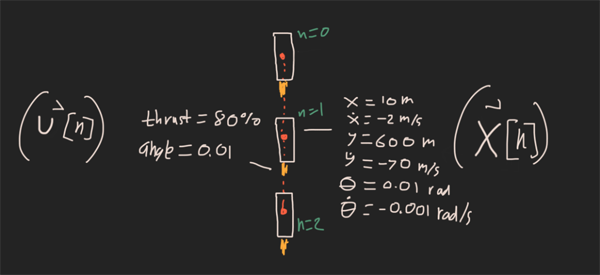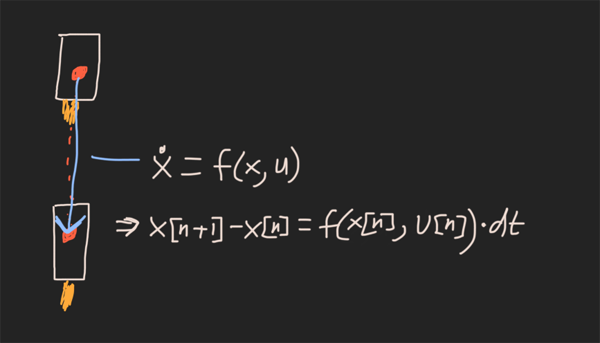为了进一步了解非线性控制,我一直在尝试一种非常有效的方法,称为轨迹优化。设置完基本代码后,就可以很容易地将其应用于各种系统。
在看完Starship SN15发射后,我决定进行一些动力学估算,以检验我的2D模拟玩具是否能执行翻转并自行着陆。令我兴奋的是,经过一番细心的研究,它运行得很好。但是真正令我惊讶的是当我与实际的着陆画面并排播放输出时:它的轨迹非常完美。而且编写整个程序和优化时我并没有参考视频或其他明确的计时信息。
对我而言有两种可能:1、我非常幸运,2、SpaceX在其实际系统上运行了非常相似的优化。这是一个非常有趣的东西,希望能为进入火箭回收后面的魔法打开一扇窗户。在开始编写代码之前,可能最好先解释一下轨迹优化的理论(但如果您愿意,也可以直接跳转至代码)。
轨迹优化:“最优轨迹”意味着什么?
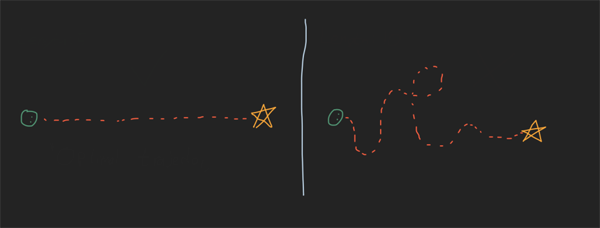
在这种情况下,“最佳”表示通常的含义:“好”,“最佳”,“理想”等。举一个简单的例子,假设您想走过整个房间到达冰箱:您可以选择看似无数的路线,但是以某种方式只能选择其中一条路线。
两条轨迹的例子
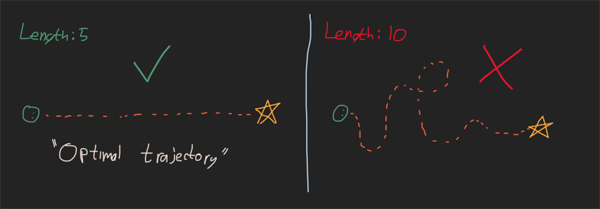
应该很容易看到有好路线和差路线,但是实际上定义好轨迹还是差轨迹的是什么呢?这就是“成本”概念进入的地方。如果您有机器学习的经验,那么这基本上是相同的概念。您运行优化以最小化成本函数。在我们的冰箱示例中,成本函数是什么?一个简单的方法就是走我们的路。现在可以要求计算机在您和冰箱之间找到一条长度最短的路径。
选择成本函数
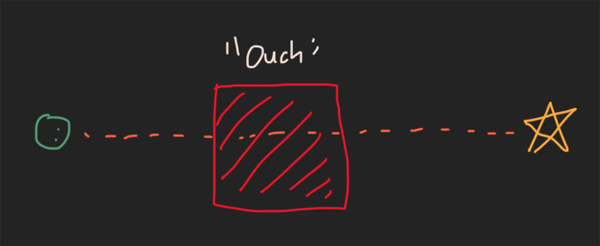
这可行,但有一些细微的缺陷。想象一下,您和冰箱之间有一个死亡陷阱。我们的“查找最小长度”算法将使您正确地进行操作,我认为您可能会认为这并不是真正的最佳选择。
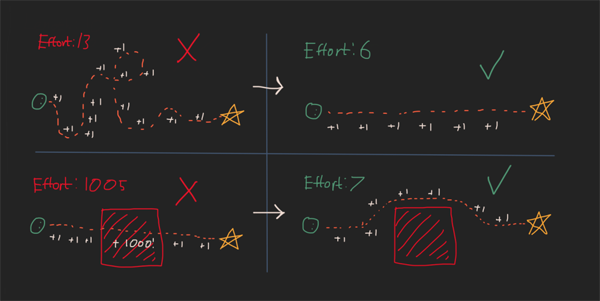
可能更好的成本函数(以及我在Starship着陆代码中主要使用的函数)基于“努力”。假设您在地板上向前迈出一步需要您付出1点努力,而经过死亡之坑™则需要您花费1000点努力。这更好地匹配了我们认为是最佳与非最佳的条件:
约束
很少有优化问题可以在没有很多约束的情况下完成,这是一些“逻辑”问题,可以解决我们的冰箱问题。
其他资料
这是轨迹优化的核心。通过最小化某些成本函数并保持一组约束来优化点之间的轨迹。这里有一些很好的资源,它们在数学方面会更深入:
https://www.youtube.com/watch?v=wlkRYMVUZTs
- 1.
为火箭着陆进行编码!
现在到有趣的东西上。有一些很棒的库可以遍历方程式并进行优化工作,因此真正的“艺术”在于向解释器提出正确的问题。下面是一个指向collab notebook的链接,可让您在浏览器中运行全部代码:
https://colab.research.google.com/drive/18MVtu4reVJLBE1RXByQEmu0O9aLXlMHz?usp=sharing
轨迹
时间被切成0.04s的块,并在每个步骤中生成了火箭状态和控制状态的变量。这导致沿路径产生一堆离散点,这些点比较容易处理,然后尝试为整个对象提出封闭形式的解决方案。
由三个点和沿着该轨迹的状态组成的轨迹的示例
火箭状态向量:x[n] = [x, x_dot, y, y_dot, theta, theta_dot]
控制状态向量:u[n] = [thrust_mag, thrust_angle]
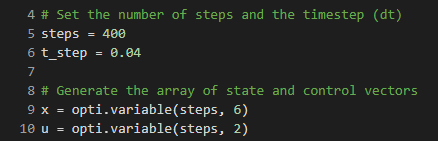
生成步骤和优化变量
之所以选择0.04s是因为它可以以每秒25帧的速度进行1:1播放。是的,实际上我确实更改了仿真时间步长,因为25 fps看起来不错。
为了找到时间步长,我手动增加了时间步长,直到找到可行的解决方案为止。有多种方法可以让求解器自行发现最短的时间轨迹(主要是:让它确定点之间的时间步长)。
成本函数
设置成本函数
所有成本都是平方和-> cost [0]²+ cost [1]²+ cost [2]²…依此类推。
最小化推力输出——理想情况下,您希望在着陆时使用少量燃油。
最小化TVC的万向节角度——移动喷嘴很费力,理想情况下,您希望它名义上指向下方。
最小化角速度——似乎有点荒唐,但我有一种直觉,即角速度/加速度会在发动机上施加最大的应变,因此您希望将其保持在尽可能低的水平。
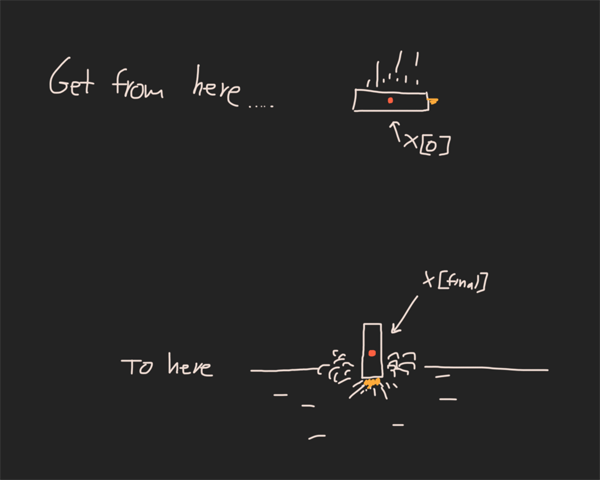
约束集1:初始条件和最终条件
初始条件是在空气中以90m / s的速度向下旋转90度然后开始向下飞行1000m。
初始条件和最终条件约束
起始高度和速度来自飞行俱乐部的SN9数据:https://flightclub.io/result/2d?code = SN91
约束集2:动态
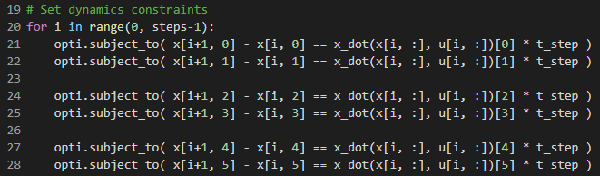
每个状态时间步都必须服从:x [n + 1] -x [n] = f(x [n],u [n])* dt
本质上,这是“不要破坏物理”的约束。它等效于火箭的离散时间模拟,下一个状态等于当前状态+导数* dt。(注意:我在代码中使用x_dot()而不是f(),因为我认为它更易于阅读)。
为状态向量中的所有元素设置动力学约束
飞行常数和动力学功能:
g = 9.8
m = 100000公斤(猜测湿重和干重之间的一个很好的舍入数。实际上,当您使用燃料时,这种情况会发生变化,但出于准确性考虑,我只是为了简单起见)
长度= 50米
I =(1/12)* m *长度²(均匀杆的惯性)
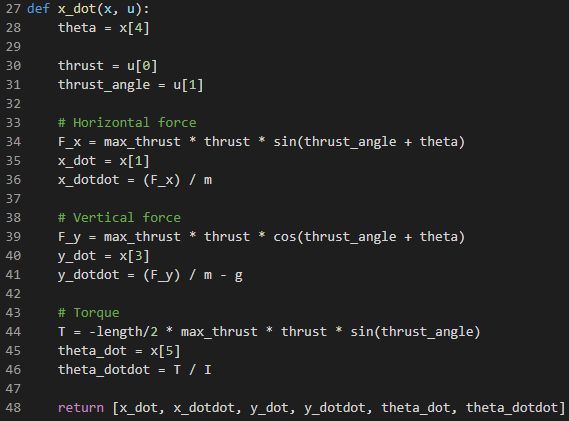
定义f(x,u)= x_dot
(注意:这是一个相当差的离散化,并且存在更好的方法,例如并置。但是,这是写出来的最简单,最快的方法)
约束集3:可变范围
推力不能超过一个猛禽战机的最大值,油门不能低于40%,推力矢量控制在每个方向上的摆角都不能超过20度 Raptor max取自维基百科,+-20度完全是个猜测,我很想知道是否有更可靠的数据用于此。
设置u的有界约束
优化!
剩下要做的就是运行它!
选择求解器并运行!
基本上就是这样,您调用opti.solve(),然后将其转换为Ipopt(开放源代码优化求解器)可以理解的问题。希望此消息应该到达大量迭代打印的底部:
这就是我们想要看到的
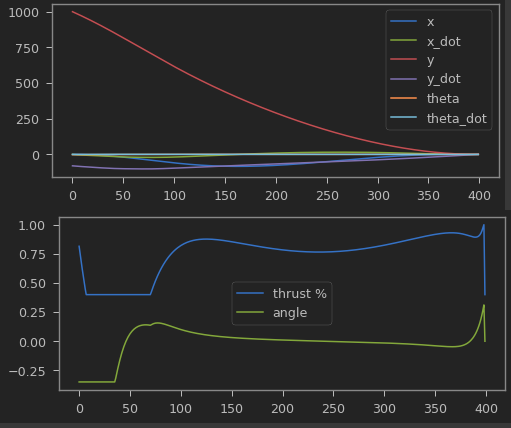
状态和控制阵列图
下一部分代码使用matplotlib制作了漂亮的动画,需要花一点时间来生成所有帧,但结果还是很不错的。
总结
虽然接近完美的轨道可能主要是让我对事物的估计感到幸运,但仍有一些有趣的东西可以借鉴,主要是:
Starship很有可能要么遵循预先计划的优化轨迹,要么运行实时优化以动态生成最优轨迹。(或两者混合)
不仅如此,我们可以进一步猜测它们的优化成本函数/“目标”与我们的非常相似:最小化推力,最小化TVC角和最小化角速度。这条赛道有时几乎是不可思议的,尤其是在双向滑行的情况下。(我一直以为这是过冲,但这可能只是到达着陆点的最佳路径)。这也是一个有趣的分析工具,我真的很想找出导致SN8和SN9着陆失败的一些其他约束(需要进行一些调整:最终状态不再是严格的约束)。
为什么实际上着陆火箭比这要难得多
“哇,我刚刚想出了SpaceX是如何着陆他们的火箭的!!”,但可悲的是,事实并非如此。
一旦生成了一条物理上可能的轨迹,该轨迹将您带到了您想去的地方,那么您需要做的很多事情才能真正沿着该轨迹运动:状态估计,闭环反馈控制,基于实际运动轨迹的动态更新时间条件……还有很多真正的航空工程师知道的东西。除此之外,这些求解器还需要花费很长时间才能运行,并且在线(实时)优化很难正确而安全地完成:一个错误的输入,您的求解器可能会发出“失败”的声音,从而导致故障发生。
下面是Lars Blackmore网站的链接,他是Starship EDL的首席工程师以及研究Falcon 9着陆技术的人。他的论文和其他出版物对如何在EDL问题中使用最佳控制进行了更为全面的概述。